Cho tứ giác ABCD. Xét hai mệnh đề
P : "Tứ giác ABCD là hình thoi"
Q : "Tứ giác ABCD có hai đường chéo vuông góc".
Phát biểu mệnh đề $\left. P\Leftrightarrow Q \right.$.
Đáp án đúng là: C
Định nghĩa mệnh đề tương đương.
Đáp án cần chọn là: C
Miền không bị gạch kể cả đường thẳng là miền nghiệm của bất phương trình nào trong bốn bất phương trình dưới đây?
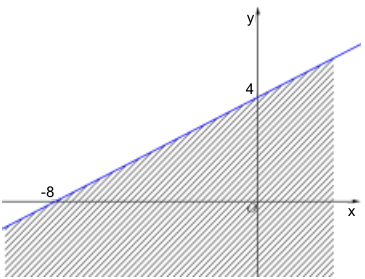
Đáp án đúng là: B
Tìm phương trình đường thẳng đi qua hai điểm $\left( {- 8;0} \right),\left( {0;4} \right)$.
Xác định miền không bị gạch kể cả đường thẳng là miền nghiệm của bất phương trình.
Đáp án cần chọn là: B
Cho tam giác ABC . Trong các khẳng định sau khẳng định nào đúng?
Đáp án đúng là: A
Công thức tính diện tích tam giác.
Đáp án cần chọn là: A
Cho $A = \left\{ 1;2;3;4 \right\},B = \left\{ 2,4,6,8 \right\}$. Tập hợp $A \cup B$ bằng
Đáp án đúng là: D
Xác định hợp của hai tập hợp.
Đáp án cần chọn là: D
Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?
Đáp án đúng là: D
Nhận biết hệ bất phương trình bậc nhất hai ẩn: Là hệ gồm hai hoặc nhiều bất phuơng trình bậc nhất hai ẩn.
Đáp án cần chọn là: D
Trên nưa đường tròn đơn vị cho điểm $M\left( {x_{0};y_{0}} \right)$ sao cho $\widehat{xOM} = \alpha$ (hình vẽ bên dưới).
Khi đó giá trị lượng giác $\tan\alpha$ bằng
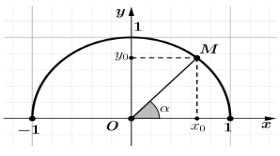
Đáp án đúng là: C
Xác định giá trị lượng giác khi bết hình biểu diễn, biết $\tan\alpha = \dfrac{\sin\alpha}{\cos\alpha}$.
Đáp án cần chọn là: C
Tìm cặp số là nghiệm của bất phương trình $- x + 3y - 2 > 0$
Đáp án đúng là: B
Thay các cặp số vào bất phương trình, kiểm tra tính thoả mãn.
Đáp án cần chọn là: B
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
Đáp án đúng là: A
Nhận biết bất phương trình bậc nhất hai ẩn.
Đáp án cần chọn là: A
Tam giác ABC có $\widehat{\text{B}} = 30^{{^\circ}},\widehat{\text{C}} = 45^{{^\circ}}$ và $\text{AB} = 5$. Tính độ dài cạnh AC .
Đáp án đúng là: B
Sử dụng định lí sin trong tam giác ABC: $\dfrac{AC}{\sin B} = \dfrac{AB}{\sin C}$
Đáp án cần chọn là: B
Cho hai tập hợp $\text{A} = \lbrack - 5;3),\text{B} = (1; + \infty)$. Khi đó $\text{A} \cap \text{B}$ là tập nào sau đây?
Đáp án đúng là: D
Xác định giao của hai tập hợp.
Đáp án cần chọn là: D
Giá trị của $\cos 60^{{^\circ}} + \sin 30^{{^\circ}}$ bằng bao nhiêu?
Đáp án đúng là: B
Tính giá trị lượng giáC.
Đáp án cần chọn là: B
Cho góc $a$ với $0^{{^\circ}} \leq a \leq 180^{{^\circ}}$. Đẳng thức nào sau đây đúng?
Đáp án đúng là: A
Sử dụng các công thức lượng giác cho hai góc bù nhau (hai góc có tổng bằng $180^{{^\circ}}$). Nếu hai góc là $\alpha$ và $180^{{^\circ}} - \alpha$, ta có:
- $\sin(180^{{^\circ}} - \alpha) = \sin\alpha$
- $\cos(180^{{^\circ}} - \alpha) = - \cos\alpha$
- $\tan(180^{{^\circ}} - \alpha) = - \tan\alpha$ (khi $\tan\alpha$ xác định)
- $\cot(180^{{^\circ}} - \alpha) = - \cot\alpha$ (khi $\cot\alpha$ xác định)
Đáp án cần chọn là: A
Cho \(A\) là tập hợp các học sinh lớp 10 đang học ở trường em và \(B\) là tập hợp các học sinh đang học môn Tiếng Anh của trường em. Khi đó:
| Đúng | Sai | |
|---|---|---|
| a) \(A \cap B\) là tập hợp các học sinh lớp 10 học môn Tiếng Anh ở trường em. | ||
| b) \(A \backslash B\) là tập hợp những học sinh lớp 10 nhưng không học Tiếng Anh ở trường em. | ||
| c) \(A \cup B\) là tập hợp các học sinh lớp 10 hoặc học sinh học môn Tiếng Anh ở trường em. | ||
| d) \(B \backslash A\) là tập hợp các học sinh học môn Tiếng Anh nhưng không học lớp 10 ở trường em. |
Đáp án đúng là: Đ; Đ; Đ; Đ
Dựa vào định nghĩa các phép toán tập hợp:
- \(A \cap B\) : phần chung của hai tập.
- \(A \backslash B\) : phần tử thuộc \(A\) mà không thuộc \(B\).
- \(A \cup B\) : hợp của hai tập.
- \(B \backslash A\) : phần tử thuộc \(B\) mà không thuộc \(A\).
Đáp án cần chọn là: Đ; Đ; Đ; Đ
An thích ăn hai loại trái cây là cam và xoài, mỗi tuần mẹ cho An 200000 đồng để mua trái cây. Biết rằng giá cam là 15000 đồng/ 1 kg , giá xoài là 30000 đồng/ 1 kg . Gọi \(x, y\) lần lượt là số ki-lô-gam cam và xoài mà An có thể mua về sử dụng trong một tuần. Khi đó:
| Đúng | Sai | |
|---|---|---|
| a) Trong tuần, số tiền An có thể mua cam là \(15000 x\), số tiền An có thể mua xoài là \(30000 y(x, y>0)\). | ||
| b) Bất phương trình bậc nhất cho hai ẩn \(x, y\) là \(3 x+6 y \geq 40\) | ||
| c) Cặp số \((5 ; 4)\) thỏa mãn bất phương trình bậc nhất cho hai ẩn \(x, y\) | ||
| d) An có thể mua 4 kg cam, 5 kg xoài trong tuần. |
Đáp án đúng là: Đ; S; Đ; S
Lập bất phương trình bậc nhất hai ẩn.
Kiểm tra nghiệm của bất phương trình.
Đáp án cần chọn là: Đ; S; Đ; S
Cho tam giác ABC có các cạnh $BC = 3~\text{cm},AC = 4~\text{cm},AB = 5~\text{cm}$. Khi đó:
| Đúng | Sai | |
|---|---|---|
| a) Tam giác ABC vuông tại C . | ||
| b) Diện tích tam giác là $12~\text{cm}^{2}$. | ||
| c) $\cos B = \dfrac{3}{5}$. | ||
| d) Chu vi của tam giác là 12 cm. |
Đáp án đúng là: Đ; S; Đ; Đ
- Kiểm tra tính vuông góc của tam giác bằng định lý Pythagoras đảo: Nếu $a^{2} + b^{2} = c^{2}$ thì tam giác vuông tại đỉnh đối diện với cạnh $c$.
- Tính cosin của góc trong tam giác bằng định lý cosin: $a^{2} = b^{2} + c^{2} - 2bc\cos A$.
- Tính chu vi tam giác: $P = a + b + c$.
Đáp án cần chọn là: Đ; S; Đ; Đ
Cho tam giác ABC biết $AB = 8$, $AC = 5$, $BC = 7$. Điểm $M$ thuộc cạnh AB sao cho $AM = 5$.
| Đúng | Sai | |
|---|---|---|
| a) $\cos B = \dfrac{1}{7}$ | ||
| b) Diện tích tam giác ABC bằng $20\sqrt{3}$. | ||
| c) Đường cao hạ từ $B$ của $\bigtriangleup ABC$ bằng $4\sqrt{3}$ | ||
| d) Bán kính đường tròn ngoại tiếp tam giác $\bigtriangleup CMB$ bằng $\dfrac{5\sqrt{3}}{3}$. |
Đáp án đúng là: S; S; Đ; S
a) Áp dụng định lý cosin trong $\bigtriangleup ABC$: $b^{2} = a^{2} + c^{2} - 2ac\cos B$ để tính cosB.
b) Sử dụng công thức Heron tính diện tích tam giác: $S_{ABC} = \sqrt{p(p - a)(p - b)(p - c)}$
c) Sử dụng công thức diện tích: $S_{ABC} = \dfrac{1}{2}b \cdot h_{b}$ để tính đường cao hạ từ B.
d) Tính CM, sau đó dùng định lí sin: $R = \dfrac{CM}{2\sin B}$ để tính bán kính R của $\bigtriangleup CMB$.
Đáp án cần chọn là: S; S; Đ; S
Xác định số phần tử của tập hợp \(A \cap B\) biết:
\(A=\{(x ; y) \mid x, y \in \mathbb{R}, y=2 x-1\}\); \(B=\{(x ; y) \mid x, y \in \mathbb{R}, y=-x+5\}\)
Đáp án đúng là:
Viết tập hợp \(A \cap B\).
\(A \cap B\) là tập hợp các cặp số \((x;y)\) thỏa mãn hệ phương trình: \(\left\{\begin{array}{l}y=2 x-1 \\ y=-x+5\end{array}\right.\)
Đáp án cần điền là: 1
Bạn Huệ mang 140000 đồng đi hiệu sách để mua vở và bút. Biết rằng giá một quyển vở là 10000 đồng và giá một cây bút là 5000 đồng. Bạn Huệ mua 9 cây bút và dành tiền còn lại để mua vở. Hỏi bạn có thể mua được tối đa bao nhiêu quyển vở?
Đáp án đúng là:
Đặt ẩn cho số quyển vở và bút bạn Huệ mua, lập bất phương trình bậc nhất hai ẩn dựa vào giá một quyển vở và một cây bút và tổng tiền Huệ có.
Thay số cây bút Huệ mua vào BTP để tìm số vở tối đa có thể mua được.
Đáp án cần điền là: 9
Để lắp đường dây điện cao thế từ vị trí A đến vị trí B , do phải tránh một ngọn núi nên người ta phải nối đường dây từ vị trí A đến vị trí C dài 15 km , sau đó nối đường dây từ vị trí C đến vị trí B dài 12 km. Góc tạo bởi hai đoạn dây AC và CB là $70^{{^\circ}}$. Dựa vào cách lắp dây điện trên, hãy tính khoảng cách từ vị trí A đến vị trí B là bao nhiêu kilomet? (Làm tròn đến hàng phần chục).
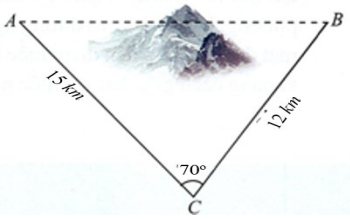
Đáp án đúng là:
Định lý cosin trong tam giác ABC: $AB^{2} = AC^{2} + CB^{2} - 2.AC.CB.\cos C$
Đáp án cần điền là: 15,7
Lớp 10A9 có 45 học sinh, trong đó mỗi học sinh giōi ít nhất một trong hai môn Toán và Văn, biết rằng có 25 bạn học giỏi môn Toán, 35 bạn học giōi môn Văn. Hỏi lớp 10A9 có bao nhiêu bạn học sinh giỏi cả hai môn Toán và Văn?
Đáp án đúng là:
Công thức $n(T \cup V) = n(T) + n(V) - n(T \cap V)$.
Đáp án cần điền là: 15
Tìm giá trị nhỏ nhất của \(F=30 x-4 y-6\) với \((x ; y)\) là nghiệm của hệ bất phương trình \(\left\{\begin{array}{l}x-y+5 \geq 0 \\ 2 x+y+4 \geq 0 \\ x+y-5 \leq 0 \\ 2 x-y-4 \leq 0\end{array}\right.\).
Đáp án đúng là:
Xác định miền nghiệm của hệ bất phương trình.
Thay toạ độ các đỉnh của đa giác vào F, tìm giá trị nhỏ nhất của F.
Đáp án cần điền là: -104
Cho tam giác ABC có $AB = 5,BC = 4,AC = 7$. Khi đó $\cos B = - \dfrac{m}{n}$, với $m,n \in {\mathbb{N}}$ và $\dfrac{m}{n}$ là phân số tối giản. Tính $m - n$.
Đáp án đúng là:
Áp dụng định lý cosin trong tam giác ABC:
$AC^{2} = AB^{2} + BC^{2} - 2 \cdot AB \cdot BC \cdot \cos B$
Đáp án cần điền là: -4