Phần 1: Tư duy Toán học
Hàm số nào sau đây nghịch biến trong khoảng (−∞;0)?
Đáp án đúng là: A
Xét tính đơn điệu của từng hàm số.
Đáp án cần chọn là: A
Cho hàm số \(f\left( x \right) = \dfrac{{\tan x + 3}}{{2\sin x + 3}}\).
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
| Đúng | Sai | |
|---|---|---|
| a) Hàm số xác định với mọi \(x \in \mathbb{R}\backslash \left\{ 0 \right\}\). |
||
| b) Các nghiệm của phương trình\(f\left( x \right) = 0\) được biểu diễn bởi 2 điểm trên đường tròn lượng giác. |
Đáp án đúng là: S; Đ
Đáp án cần chọn là: S; Đ
Kéo biểu thức ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
Hàm số $y = \sin x + \cos x$ tuần hoàn với chu kì
Hàm số $y = \cot x$ xác định với mọi x thuộc khoảng
Đáp án đúng là: \(2\pi\); \(\left( {\dfrac{\pi }{2};\pi } \right)\)
Hàm $\sin x; \cos x$ tuần hoàn chu kì $2\pi$; hàm $\tan x; \cot x$ tuần hoàn chu kì $\pi$
Hàm $f(x)$ tuần hoàn chu kì a, hàm $g(x)$ tuần hoàn chu kì b thì hàm $f(x)+g(x)$ tuần hoàn chu kì BCNN(a;b)
Đáp án cần chọn là: \(2\pi\); \(\left( {\dfrac{\pi }{2};\pi } \right)\)
Trong các số có ba chữ số khác nhau được lập từ các số $\left\{ \left. {1,2,3,4,5,6} \right\} \right.$, số các số chia hết cho 3 bằng:
Đáp án đúng là: A
Dấu hiệu chia hết cho 3: Số chia hết cho 3 là số có tổng các chữ số chia hết cho 3.
Chọn ra các bộ 3 chữ số khác nhau có tổng chia hết cho 3 và lập số có 3 chữ số khác nhau từ mỗi bộ ấy.
Đáp án cần chọn là: A
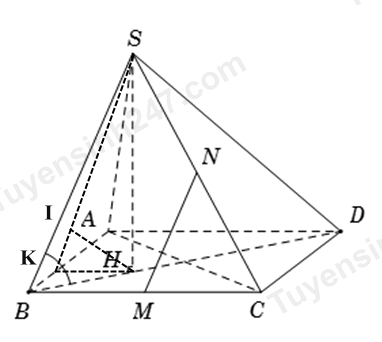
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh a và BD = a. Biết cạnh $SA = \dfrac{a\sqrt{6}}{2}$ và vuông góc với mặt phẳng (ABCD).
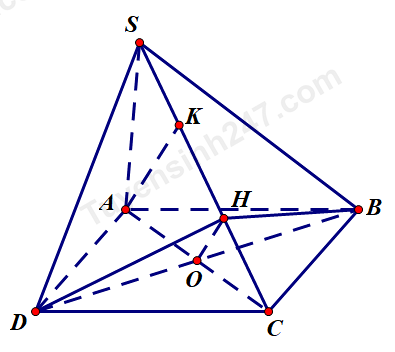
Hướng dẫn cách chứng minh $(SCD)\bot(SBC)$ bị thiếu một số chỗ.
Hãy kéo ô thích hợp vào vị trí tương ứng:
Dựng $OH\bot SC$.
Do \(SA \bot \left( {ABCD} \right)\) nên $SA\bot$
Mà $\bot BD$ nên $BD\bot(SAC)$. Suy ra $BD\bot$ .
Mặt khác $\bot SC$ nên $SC\bot(DHB)$.
Như vậy $\widehat{DHB}$ là góc giữa hai mặt phẳng $(SCD)$ và $(SBC)$.
Tam giác $ABD$ đều cạnh $a$ nên $AO =$ \(\frac{{a\sqrt 3 }}{2}\) $\left. \Rightarrow AC = \right.$ .
Dựng $\left. AK\bot SC\Rightarrow AK = \right.$ a $\left. \Rightarrow OH = \dfrac{AK}{2} = \dfrac{a}{2} \right.$.
Tam giác $DHB$ có đường trung tuyến $HO =$$BD$ \(=\frac{a}{2}\).
$\left. \Rightarrow\Delta DHB \right.$ vuông tại $H$ hay $\widehat{DHB} = 90{^\circ}$. Do đó $(SCD)\bot(SBC)$.
Đáp án đúng là: $BD$; \(AC\); $SC$; $OH$; \(a\sqrt 3 \); \(\frac{1}{2}\)
Hai mặt phẳng vuông góc
Đáp án cần chọn là: $BD$; \(AC\); $SC$; $OH$; \(a\sqrt 3 \); \(\frac{1}{2}\)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với $AB = a,AD = a\sqrt{3}$. Hình chiếu vuông góc $H$ của $S$ trên mặt đáy trùng với trọng tâm tam giác ABC và $SH = \dfrac{a}{2}$. Gọi M, N lần lượt là trung điểm các cạnh BC và SC. Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
| Đúng | Sai | |
|---|---|---|
| a) Khoảng cách từ $MN$ tới $SA$ bằng $\dfrac{3a\sqrt{7}}{14}$. | ||
| b) Tan góc giữa đường thẳng MN với mặt đáy $(ABCD)$ bằng $\dfrac{2}{3}$. |
Đáp án đúng là: Đ; S
Sử dụng các mối quan hệ hình học đã biết kết hợp với cách xác định góc giữa đường thẳng và mặt phẳng để tìm góc giữa MN với mặt đáy (ABCD).
Góc giữa đường thẳng và mặt phẳng.
Đáp án cần chọn là: Đ; S
Đồ thị $(P)$ của một hàm số bậc hai $y = f(x)$ đã bị xoá đi, chỉ còn lại trục đối xứng $\Delta$, điểm $A$ thuộc $(P)$ và tiếp tuyến tại $A$ của $(P)$ được cho dưới đây:
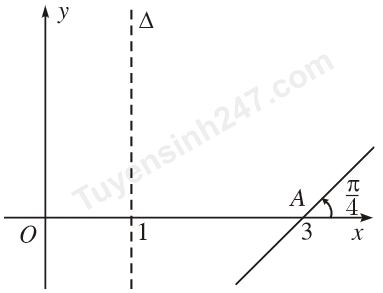
Đồ thị hàm số $y = f(x)$ đi qua những điểm nào trong các điểm sau?
Đáp án đúng là: A; C
Đa thức phải tìm có dạng :
$P(x) = ax^{2} + bx + c(a \neq 0)$
Lập hệ và giải.
Đáp án cần chọn là: A; C
Trong không gian Oxyz, có bao nhiêu điểm I cùng cách ba mặt phẳng tọa độ (Oxy), (Oyz), (Ozx) một khoảng bằng 2024?
Đáp án đúng là: C
Gọi $I(x,y,z)$ là điểm cùng cách ba mặt phẳng tọa độ (Oxy), (Oyz), (Ozx) một khoảng bằng 2024.
Khi đó $|x|=|y|=|z|=2024$ Từ đó tìm x, y, z thoả mãn
Đáp án cần chọn là: C
Cho đồ thị của các hàm số tuần hoàn trên tập xác định $\mathbb{R}$:
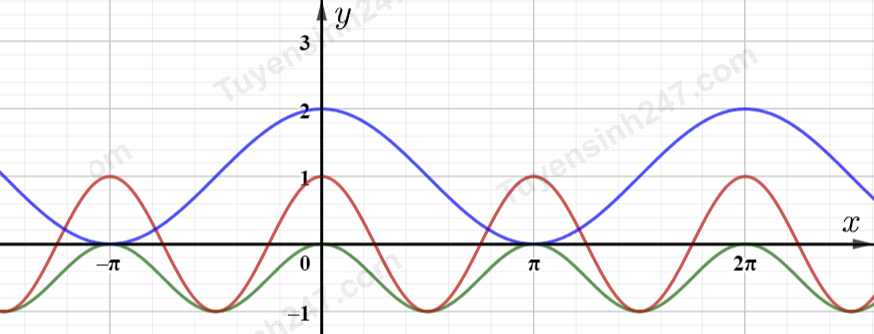
Có bao nhiêu đồ thị thỏa mãn $f\left( {x + k\pi} \right) = f(x)\,\,\forall k \in {\mathbb{Z}};\,\, x \in {\mathbb{R}}$.
Đáp án đúng là: 2
Hàm số tuần hoàn với chu kì $\pi$ thì $f\left( {x + k\pi} \right) = f(x)\,\,\forall k \in {\mathbb{Z}};\,\, x \in {\mathbb{R}}$.
Đáp án cần điền là: 2
Số $n = 50!$ có bao nhiêu chữ số 0 liên tiếp ở tận cùng phía bên phải?
Đáp án đúng là: B
Tìm số các số chia hết cho 5 khi nhân với 1 số chẵn ta được 1 số tận cùng là 1 số 0
Đặc biệt số 25, 50 khi nhân với 1 số chẵn được tận cùng là 2 số 0
Đáp án cần chọn là: B
Tìm tất cả các giá trị thực của tham số m để bất phương trình sau có nghiệm:
$\left( {x\sqrt{x} + \sqrt{x + 12}} \right) \leq m.\log_{5 - \sqrt{4 - x}}3$.
Đáp án đúng là: B
BPT $\left. \Leftrightarrow f(x) = \log_{3}\left( {5 - \sqrt{4 - x}} \right).\left( {x\sqrt{x} + \sqrt{x + 12}} \right) \leq m \right.$
BPT có nghiệm $\left. \Rightarrow m \geq \min\limits_{\lbrack{0;4}\rbrack}f(x) \right.$
Chứng minh hàm $f(x)$ đồng biến trên (0;4) từ đó suy ra GTNN của $f(x)$
Đáp án cần chọn là: B
Cho biểu thức $f(x) = (x - 1)(x - 2)(x - 3)...(x - 20)$ với $x \in Z$ và S là tập hợp tất cả các số nguyên x để $f(x)$ đạt giá trị nhỏ nhất
Kéo các ô sau thả vào vị trí thích hợp để được khẳng định đúng:
Giá trị nhỏ nhất của $f(x)$ là
Số phần tử của S là
Đáp án đúng là: 0; 20
Xét các trường hợp: $x \leq 0$, $x \geq 21$ và $0 < x < 20.$
Đáp án cần chọn là: 0; 20
Một cầu thang đường lên cổng trời của một điểm giải trí ở công viên tỉnh X được hàn bằng sắt có hình dáng các bậc thang đều là hình chữ nhật với cùng chiều rộng là 35cm và chiều dài của nó theo thứ tự mỗi bậc đều giảm dần đi 7cm. Biết rằng bậc đầu tiên của cầu thang là hình chữ nhật có chiều dài 189cm và bậc cuối cùng cầu thang là hình chữ nhật có chiều dài 63cm. Hỏi giá thành làm cầu thang đó gần với số nào dưới đây nếu giá thành làm một mét vuông cầu thang đó là 1250 000 đồng trên một mét vuông?
Đáp án đúng là: D
Cấp số cộng
Đáp án cần chọn là: D
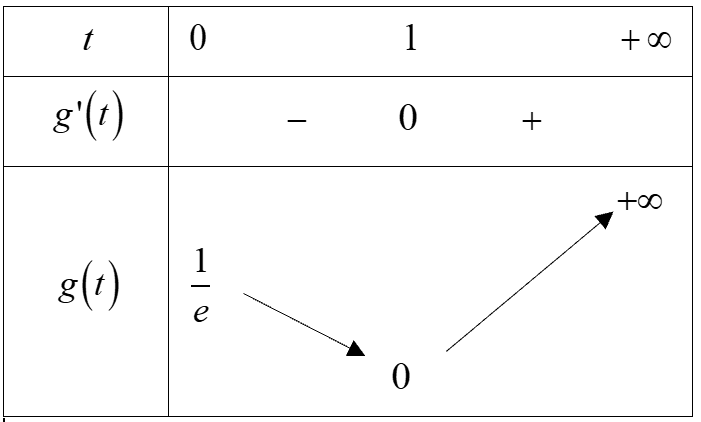
Xét hàm số $f(t) = \dfrac{9^{t}}{9^{t} + m^{2}}$ với m là tham số thực. Gọi S là tập hợp tất cả các giá trị của m sao cho $f(x) + f(y) = 1$ với mọi số thực x, y thỏa mãn $e^{x + y} \leq e\left( {x + y} \right)$. Tìm số phần tử của S.
Đáp án đúng là: B
Đặt t = x + y. Chứng minh $g(t) = e^{t - 1} - t \le 0$ nên $e^{t - 1} = t$ khi t = 1 suy ra $x+y=1$
Từ $x+y=1$ thay vào $f(x) + f(y) = 1$ tìm m
Đáp án cần chọn là: B
Có bốn ngăn (trong một giá để sách) được đánh số thứ tự $1,2,3,4$ và tám quyển sách khác nhau. Bạn An xếp hết tám quyển sách nói trên vào bốn ngăn đó sao cho mối ngăn có ít nhất một quyển sách và các quyển sách được xếp thẳng đứng thành một hàng ngang với gáy sách quay ra ngoài ở mỗi ngăn. Khi đã xếp xong tám quyển sách, hai cách xếp của bạn An được gọi là giống nhau nếu chúng thỏa mãn đồng thời hai điều kiện sau đây:
Với từng ngăn, số lượng quyển sách ở ngăn đó là như nhau trong cả hai cách xếp.
Với từng ngăn, thứ tự từ trái sang phải của các quyển sách được xếp là như nhau trong cả hai cách xếp.
Gọi $T$ là số cách xếp đôi một khác nhau của bạn An. Giá trị của $\dfrac{T}{600}$ bằng bao nhiêu?
Đáp án đúng là: 2352
Tìm số các xếp sách chia vách ngăn, 7 cuốn có 6 vách ngăn từ đó tìm số cách xếp
Đáp án cần điền là: 2352
Cho hàm số $f(x) = x^{4} + 4mx^{2} - 2m^{2} + 24.$ Có bao nhiêu giá trị nguyên của $m \in \left( {- 50;50} \right)$ để hàm số $y = \left| {f(x)} \right|$ có $3$ điểm cực trị.
Đáp án đúng là: D
Số điểm cực trị của $y = \left| {f(x)} \right|$=Số điểm cực trị của $y = f(x)$+ Số nghiệm bội lẻ của $f(x) = 0$.
Đáp án cần chọn là: D
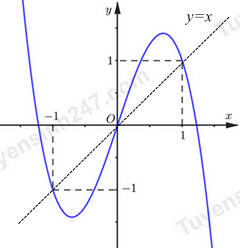
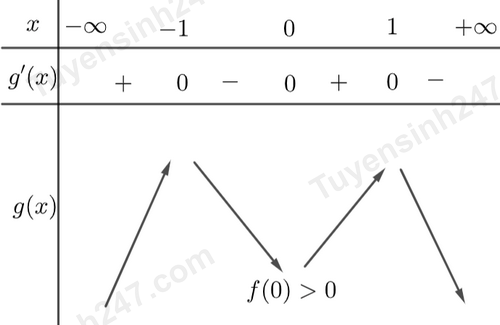
Cho hàm số $f(x)$ liên tục và có đạo hàm trên ${\mathbb{R}}.$ Biết $f(0) > 0.$ Đồ thị hàm số $y = f'(x)$ như hình vẽ:
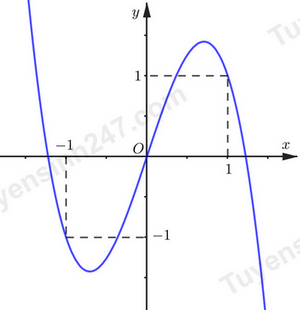
Hàm số $y = \left| {f(x) - \dfrac{x^{2}}{2}} \right|$ có bao nhiêu điểm cực trị?
Đáp án đúng là: C
Số điểm cực trị của $y = \left| {f(x)} \right|$=Số điểm cực trị của $y = f(x)$+ Số nghiệm bội lẻ của $f(x) = 0$.
Đáp án cần chọn là: C
Số thập phân vô hạn tuần hoàn \(0,271414 \ldots \) viết dạng phân số có dạng \(\dfrac{m}{n}\) với m; n là các số tự nhiên và \(\dfrac{m}{n}\) là phân số tối giản. Tính \(n - 3m\)
Đáp án đúng là: 1839
Đáp án cần điền là: 1839
Cho hai số thực không âm $x,y$ thỏa mãn $x^{2} - 2x - y = 3.$ Tìm giá trị nhỏ nhất của biểu thức $P = xy + \dfrac{3}{2}x^{2} - 7x + 3y + 10.$
Đáp án đúng là: A
Từ $x^{2} - 2x - y = 3$ rút y theo x để tìm điều kiện của x sau đó thay vào P
Khảo sát hàm số P(x) tìm GTNN
Đáp án cần chọn là: A
Một con lắc lò xo dao động điều hoà theo phương ngang trên mặt phẳng không ma sát, có phương trình dao động $x(t) = 10\sin\left( {\dfrac{2\pi}{3}t + \dfrac{3\pi}{5}} \right) + 3$, trong đó x tính bàng centimét và thời gian t tính bằng giây. Chọn các khẳng định đúng.
Đáp án đúng là: A; C
a) Thay $x = 0$ và tính $x(t)$
b) Tính đạo hàm của $x(t)$
c) Tính $x'(8)$
d) Giải phương trình $x'(t) = 0$
Đáp án cần chọn là: A; C
Cho $f(x) = \dfrac{1 - 3x + x^{2}}{x - 1}$. Tập nghiệm của phương trình $f'(x) > 0$ là:
Đáp án đúng là: D
Rút gọn $f(x) = \dfrac{1 - 3x + x^{2}}{x - 1} = x - 2 - \dfrac{1}{x - 1},$sau đó đạo hàm và giải bất phương trình.
Đáp án cần chọn là: D
Cho hình chóp $S.ABC$ có đáy là tam giác vuông tại $A$, cạnh huyền $BC = 6(cm)$, các cạnh bên cùng tạo với đáy một góc $60^{0}$.
Kéo biểu thức trong các ô thả vào vị trí thích hợp trong các câu sau:
Các cạnh bên của hình chóp bằng
Diện tích mặt cầu ngoại tiếp hình chóp $S.ABC$ bằng
Đáp án đúng là: 6cm; 48\(\pi\) \(cm^2\)
a) Gọi H là tâm đáy. Chứng minh SH vuông góc đáy từ đó tính độ dài các cạnh bằng pythago
b) Trong $\Delta SAH$ dựng trung trực của $SA$ cắt $SH$ tại $I$.
Khi đó $IA = IB = IC = IS$. Vậy $I$ là tâm mặt cầu ngoại tiếp hình chóp $S.ABC$.
Từ đó tính độ dài SI và diện tích mặt cầu
Đáp án cần chọn là: 6cm; 48\(\pi\) \(cm^2\)
Trong không gian $Oxyz$ cho các vectơ $\overset{\rightarrow}{a}(1;0; - 2)$, $\overset{\rightarrow}{b}( - 1; - 1;3)$ và $\overset{\rightarrow}{c}(2;3; - 1)$. Gọi giá trị của $\left( {2\overset{\rightarrow}{a} - \overset{\rightarrow}{b}} \right)\overset{\rightarrow}{c}$ bằng $A$. Những mệnh đề nào dưới đây là đúng?
Đáp án đúng là: A; D
- Sử dụng tích vô hướng.
Đáp án cần chọn là: A; D
Tập nghiệm của bất phương trình $\log_{\dfrac{1}{3}}x^{2} > \log_{\dfrac{1}{\sqrt{3}}}(x + 2)$ là:
Đáp án đúng là: B
Công thức cơ bản $\log_{a}x > \log_{a}y$ suy ra x < y khi 0<a<1
Đáp án cần chọn là: B
Cho hàm số $y = f(x) = \text{log}_{2}\left( {1 + 2^{x}} \right)$. Tính giá trị $S = f'(0) + f'(1)$.
Đáp án đúng là: C
Công thức đạo hàm cơ bản
Đáp án cần chọn là: C
Điền một số nguyên dương thích hợp vào chỗ trống.
Xét số $A = 123456789101112...20232024$ (số tự nhiên $A$ có được bằng cách viết lần lượt các số từ $\left. 1\rightarrow 2024 \right.$). Số dư của $A$ khi chia cho $45$ bằng ______ .
Đáp án đúng là: 9
Xét tổng $A = 1 + 2 + .. + 2024$ có $\left\{ \begin{array}{l} {A - 9 \vdots 5} \\ {A - 9 \vdots 9} \end{array} \right.$ từ đó suy ra A chia 45 dư 9
Đáp án cần điền là: 9
Người ta thực hiện thí nghiệm cho hai quả bóng A và B di chuyển ngược chiều nhau và va chạm với nhau. Sau va chạm, mỗi quả bóng di chuyển ngược lại một đoạn thì dừng hẳn. Biết sau khi va chạm, quả bóng A di chuyển ngược lại với vận tốc $v_{A}(t) = 10 - 2t(m/s)$ và quả bóng B di chuyển ngược lại với vận tốc $v_{B}(t) = 12 - 4t(m/s)$. Giả sử hai quả bóng đều chuyển động thẳng.
Kéo thả vào vị trí tương ứng:
Quãng đường đi được của quả cầu A từ lúc va chạm đến khi dừng hẳn là
Khoảng cách giữa hai quả bóng sau khi dừng hẳn là
Đáp án đúng là: 25; 43
Vật dừng hẳn khi vận tốc bằng 0 từ đó tính quãng đường bằng tích phân
Đáp án cần chọn là: 25; 43
Cho A là tập hợp các số tự nhiên có 6 chữ số. Chọn ngẫu nhiên một số thuộc tập hợp A. Tính xác suất để số tự nhiên được chọn chia hết cho 13 và có chữ số tận cùng bằng 2.
Đáp án đúng là: A
Gọi $a_{1} < a_{2} < ... < a_{n}$ là các số tự nhiên có 6 chữ số, các số đều chia hết cho 13 và có chữ số tận cùng bằng 2.
Khi đó $a_{1},a_{2},...,a_{n}$ lập thành một cấp số cộng với $a_{1} = 100022$ và công sai $d = 130$.
Lập công thức tổng quát của cấp số cộng và giải bất phương trình $a_{n}<10^6$ tìm n
Đáp án cần chọn là: A
Hệ nhị phân gốc 2 (hay hệ đếm cơ số hai) là một hệ đếm dùng hai ký tự 0 và 1 để biểu đạt một giá trị số. Ví dụ $100101_{2}$ (ký hiệu viết nhỏ phía dưới ám chỉ gốc nhị phân). Trong hệ nhị phân, giá trị 10 có thể biểu đạt bằng hình thức tương tự: $\left( 1.2^{1} \right) + \left( 0.2^{0} \right) = 2 + 0$, giá trị này bằng 2 trong hệ thập phân nên ta viết $10_{2} = 2_{10}$
Tương tự, ta có các ví dụ chuyển từ hệ nhị phân sang hệ thập phân:
$1_{2} = 1.2^{0} = 1.1 = 1_{10}$
$101_{2} = \left( 1.2^{2} \right) + \left( 0.2^{1} \right) + \left( 1.2^{0} \right) = 4 + 0 + 1 = 5_{10}$
$110101_{2} = \left( 1.2^{5} \right) + \left( 1.2^{4} \right) + \left( 0.2^{3} \right) + \left( 1.2^{2} \right) + \left( 0.2^{1} \right) + \left( 1.2^{0} \right) = 32 + 16 + 0 + 4 + 0 + 1 = 53_{10}$
Trong số trong hệ nhị phân gốc 2 dưới đây, số nào khi chuyển sang hệ thập phân được giá trị chia hết cho 7?
Đáp án đúng là: A
Đáp án cần chọn là: A
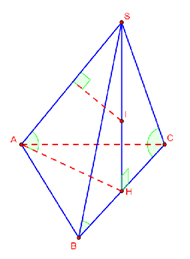
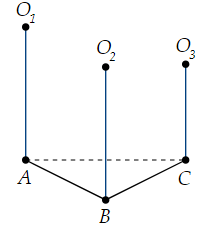
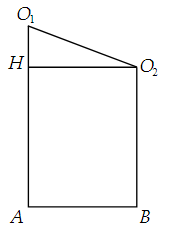
Cho ba hình cầu tiếp xúc ngoài nhau từng đôi một và cùng tiếp xúc với một mặt phẳng. Các tiếp điểm của các hình cầu trên mặt phẳng lập thành tam giác có các cạnh bằng 4, 2 và 3. Tích bán kính của ba hình cầu trên bằng
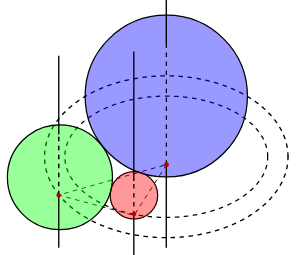
Đáp án đúng là: D
Đáp án cần chọn là: D
Có bao nhiêu số nguyên $a$ sao cho ứng với mỗi $a$, tồn tại ít nhất 8 số nguyên $b \in ( - 10;10)$ thỏa mãn: $5^{a^{2} - 2a - 3 + b} \leq 3^{b + a} + 598$.
Đáp án đúng là: 7
Đáp án cần điền là: 7
Cho hàm số $y = f(x)$ có bảng biến thiên như sau:
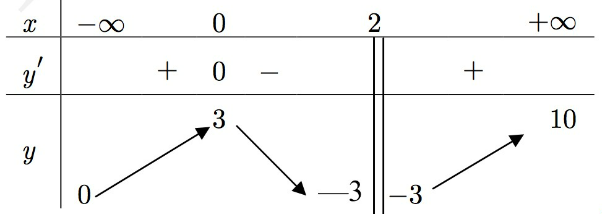
Kéo ô thích hợp thả vào các vị trí để có mệnh đề đúng:
1) Hàm số đã cho có điểm cực trị.
2) Hàm số đã cho đạt cực đại tại điểm có hoành độ bằng .
3) Đồ thị hàm số đã cho có tổng cộng đường tiệm cận đứng và ngang.
Đáp án đúng là: 1; 0; 2
Xét từng mệnh đề.
Đáp án cần chọn là: 1; 0; 2
Gọi $m_{0}$ là giá trị thực của tham số m để giá trị nhỏ nhất của hàm số $y = \dfrac{x - m^{2}}{x + 4}$ trên đoạn [0;5] bằng -1. Khi đó, giá trị của $m_{0}$ có thể thuộc những khoảng nào trong các khoảng sau?
Đáp án đúng là: B; D
Chứng minh hàm số luôn đơn điệu trên các khoảng xác định, từ đó xác định giá trị nhỏ nhất của hàm số.
Đáp án cần chọn là: B; D
Giá trị của giới hạn $L = \lim\left\lbrack {\left( {1 - \dfrac{1}{2^{2}}} \right)\left( {1 - \dfrac{1}{3^{2}}} \right)...\left( {1 - \dfrac{1}{n^{2}}} \right)} \right\rbrack$ bằng $\dfrac{a}{b}$ (phân số tối giản). Khi đó, tổng $a + b$ bằng:
Đáp án đúng là: 3
Xét dãy số $\left( u_{n} \right)$, với $u_{n} = \left( {1 - \dfrac{1}{2^{2}}} \right)\left( {1 - \dfrac{1}{3^{2}}} \right)\ldots\left( {1 - \dfrac{1}{n^{2}}} \right),n \geq 2,n \in {\mathbb{N}}$.
Sử dụng phương pháp quy nạp để tìm SHTQ của dãy số \(u_n\).
Sử dụng quy tắc tính giới hạn hàm phân thức, từ đó xác định được a và b.
Đáp án cần điền là: 3
Điểm đối xứng của điểm $M( - 2;3;4)$ qua mặt phẳng $(Oxy)$ là điểm $M'$ có cao độ bằng:
Đáp án đúng là: -4
Điểm đối xứng của điểm $M(a;b;c)$ qua mặt phẳng $(Oxy)$ là điểm $M'(a;b;-c)$.
Đáp án cần điền là: -4
Hình vẽ bên dưới là hai bánh răng của một động cơ, chúng có cùng kích thước. Khi động cơ hoạt động, hai bánh răng quay đều, cùng chiều. Biết tốc độ quay của bánh răng ở hình 2 gấp ba tốc độ quay của bánh răng ở hình 1 và phương trình biểu thị độ cao của điểm $A$ ở bánh răng thứ nhất là $h = 2R + R\text{sin}\left( {\dfrac{\pi}{5}t} \right)$ (trong đó $R$ là bán kính bánh răng, $t$ là thời gian tính bằng phút, $h$ là độ cao của điểm $A$). Giả sử tại thời điểm bắt đầu khởi động, hai điểm $A,B$ có độ cao bằng nhau và tâm của hai bánh răng $O_{1},O_{2}$ ở độ cao $2R$ so với mặt đất. Tìm thời điểm đầu tiên sau khi động cơ hoạt động hai điểm $A,B$ có độ cao bằng nhau. Nhập kết quả dưới dạng phân số a/b.
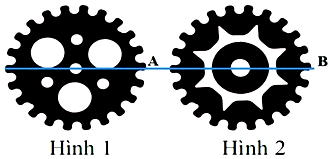
Đáp án đúng là: 5/4
Vì hai bánh răng có cùng kích thước, tốc độ của bánh răng thứ hai gấp ba tốc độ của bánh răng thứ nhất và tại thời điểm ban đầu, hai điểm $A,B$ có độ cao bằng nhau nên phương trình biểu thị độ cao của điểm $B$ là $h' = 2R + R\text{sin}\left( {\dfrac{3\pi}{5}t} \right)$.
Hai điểm $A,B$ có độ cao bằng nhau khi $h = h'$. Giải phương trình tìm nghiệm t nguyên dương nhỏ nhất.
Đáp án cần điền là: 5/4
Cho dãy số $\left( u_{n} \right)$ xác định bởi $\left\{ {\begin{array}{*{20}{l}} {{u_1} = 1}\\ {{u_{n + 1}} = \sqrt {3u_n^2 + 2} {\mkern 1mu} ;{\mkern 1mu} n \ge 1} \end{array}} \right.$. Tính tổng $S = u_{1}^{2} + u_{2}^{2} + u_{3}^{2} + ... + u_{2022}^{2}$:
Đáp án đúng là: A
Đáp án cần chọn là: A
Cho hàm số $f(x) = \dfrac{mx + 2}{x + 1}$ có đạo hàm liên tục trên ${\mathbb{R}}\backslash\left\{ {- 1} \right\}$ sao cho $df(3) = 1dx$. Giá trị của $m$ là:
Đáp án đúng là: A
Từ giả thiết $\left. df(3) = 1dx$ tính f'(3).
Tính đạo hàm của hàm số đã cho, sau đó cũng tính f'(3).
Giải phương trình tìm m.
Đáp án cần chọn là: A
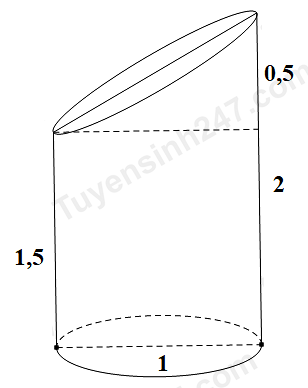
Một khối gỗ hình trụ có đường kính 1m và chiều cao 2m. người ta đã cắt khối gỗ , phần còn lại của hình vẽ bên có thể tích là V. Hãy tính V.
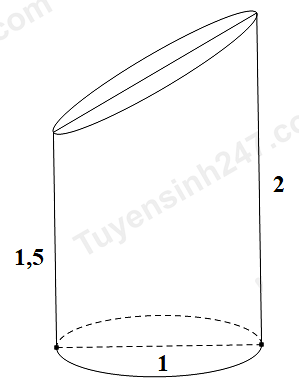
Đáp án đúng là: D
Gọi $V_{1},V_{2}$ lần lượt là thể tích khối gỗ ban đầu và thể tích khối gỗ bị cắt, tính $V_{1},V_{2}$
Tính thể tích khối gỗ còn lại là $V = V_{1} - V_{2}.
Đáp án cần chọn là: D
Trong không gian $Oxyz$, cho ba điểm $A\left( {1;1;1} \right),B\left( {- 1;1;0} \right),C\left( {3;1; - 1} \right).$ Gọi $M\left( {a;b;c} \right)$ là điểm thuộc mặt phẳng $\left( {Oxz} \right)$ và cách đều ba điểm $A,B,C$. Khi đó, $a + b - c$ bằng
Đáp án đúng là: D
M cách đều ba điểm $A,B,C$ nên M thuộc đồng thời mặt phẳng trung trực của AB và AC.
Lập phương trình mặt phẳng trung trực của AB và AC.
Xác định toạ độ điểm M là giao điểm 3 mặt phẳng: mặt phẳng trung trực của AB, mặt phẳng trung trực của AC, mặt phẳng (Oxz).
Đáp án cần chọn là: D
Phần 2: Tư duy đọc hiểu
Đọc văn bản sau và trả lời các câu hỏi từ 1 đến 10:
ĐẢM BẢO AN TOÀN CHO TRẺ EM TRONG THỜI ĐẠI AI
[1] Hiện nay, rất ít nhà phát triển AI có chính sách rõ ràng về việc đảm bảo an toàn cho trẻ em khi sử dụng công nghệ mới mẻ này. Trẻ em ngày nay tiếp xúc nhiều với các thiết bị điện tử và phần mềm tự động, tuy nhiên, những sự cố xảy ra đã đặt ra câu hỏi lớn về an toàn của trẻ khi tương tác với các công nghệ này.
[2] Một sự cố nổi bật xảy ra vào năm 2021 khi Alexa, trợ lý giọng nói AI của Amazon, đã đề xuất cho một đứa trẻ 10 tuổi chạm đồng xu vào phích cắm điện. Đứa trẻ yêu cầu Alexa đưa ra một "thử thách" và nhận được phản hồi nguy hiểm này. May mắn thay, mẹ của đứa bé đã can thiệp kịp thời. Đây không phải là trường hợp duy nhất. Năm ngoái, My AI của Snapchat cũng cung cấp lời khuyên không phù hợp cho một bé gái 13 tuổi (do một nhà nghiên cứu trưởng thành đóng giả). Dù các công ty phản ứng bằng cách sửa lỗi và cải tiến biện pháp an toàn, nhưng theo các nhà nghiên cứu, cần có biện pháp chủ động hơn để đảm bảo AI an toàn cho trẻ em ngay từ đầu.
[3] TS. Nomisha Kurian từ Đại học Cambridge cho rằng trẻ em thường bị bỏ qua khi phát triển AI. Hiện nay, rất ít nhà phát triển và công ty có chính sách rõ ràng về vấn đề này. TS. Kurian đã nghiên cứu các tương tác giữa AI và trẻ em để phát hiện những rủi ro tiềm ẩn. Bà nhận thấy các mô hình ngôn ngữ lớn (LLM) thường không thể hiểu rõ các khía cạnh trừu tượng, cảm xúc, và khó đoán định trong cuộc trò chuyện với trẻ em. Điều này có thể dẫn đến các phản hồi không an toàn.
[4] Các chatbot AI có khả năng ngôn ngữ ấn tượng nhưng lại gặp khó khăn trong việc thấu hiểu và phản hồi với cảm xúc của trẻ em. Hơn nữa, trẻ em thường có xu hướng tiết lộ thông tin cá nhân nhiều hơn và coi chatbot như “người” hơn người lớn, điều này tạo ra nhiều nguy cơ. Nghiên cứu cũng chỉ ra rằng trẻ em sử dụng chatbot thường không được giám sát chặt chẽ. Một nghiên cứu của Common Sense Media cho thấy 50% học sinh từ 12 đến 18 tuổi đã sử dụng Chat GPT cho việc học, nhưng chỉ có 26% phụ huynh biết điều này. TS. Kurian không cho rằng cần cấm AI, mà cần làm cho nó an toàn hơn. Bà đề xuất một khuôn khổ gồm 28 câu hỏi để các công ty, giáo viên, phụ huynh và nhà phát triển AI suy nghĩ một cách hệ thống về cách giữ an toàn cho người dùng trẻ tuổi khi họ tương tác với các chatbot AI.
[5] Tóm lại, có nhiều lý do khiến nhiều AI hiện tại chưa an toàn cho trẻ em. Dưới đây là một số lý do chính:
- Nội dung không phù hợp: AI có thể truy cập và hiển thị nội dung không phù hợp với trẻ em, chẳng hạn như nội dung bạo lực, ngôn ngữ không phù hợp, hoặc thông tin nhạy cảm.
- Quyền riêng tư và bảo mật: Trẻ em có thể không hiểu rõ về tầm quan trọng của việc bảo vệ thông tin cá nhân. AI thu thập dữ liệu mà không có sự kiểm soát và bảo mật thích hợp có thể dẫn đến việc lộ thông tin cá nhân của trẻ em.
- Tương tác không an toàn: AI chatbot hoặc trợ lý ảo có thể bị lạm dụng bởi những kẻ xấu, sử dụng để lừa gạt hoặc gây hại cho trẻ em thông qua các tương tác không an toàn.
- Thiếu kiểm soát nội dung: Nhiều hệ thống AI không có cơ chế kiểm soát nội dung hiệu quả, dẫn đến việc hiển thị các thông tin không chính xác, thiếu kiểm chứng hoặc mang tính định hướng tiêu cực.
- Ảnh hưởng tâm lý và hành vi: Trẻ em dễ bị ảnh hưởng bởi các nội dung và tương tác mà AI cung cấp. Điều này có thể dẫn đến những tác động tiêu cực về tâm lý và hành vi, chẳng hạn như giảm khả năng tư duy sáng tạo hoặc tạo ra những thói quen xấu.
- Thiếu quy định và hướng dẫn: Hiện nay, các quy định và hướng dẫn về việc sử dụng AI cho trẻ em vẫn còn hạn chế. Điều này dẫn đến việc các nhà phát triển AI không tuân thủ các tiêu chuẩn an toàn cần thiết.
[6] Việc bảo đảm an toàn cho trẻ em khi sử dụng AI không chỉ là trách nhiệm của các công ty công nghệ mà còn cần sự phối hợp của toàn xã hội. Bằng cách áp dụng những biện pháp chủ động và hợp lý, chúng ta có thể bảo vệ trẻ em khỏi những nguy cơ tiềm ẩn và giúp chúng tận dụng tối đa lợi ích từ công nghệ mới mẻ này. Để bảo vệ trẻ em, cần có sự hợp tác giữa các nhà phát triển công nghệ, phụ huynh, nhà giáo dục và các cơ quan quản lý để đảm bảo rằng AI được thiết kế và sử dụng một cách an toàn và có trách nhiệm.
P.A.T (NASATI), theo https://www.forbes.com/, 8/2024)
Trả lời cho các câu 41, 42, 43, 44, 45, 46, 47, 48, 49, 50 dưới đây:
Nội dung chính của văn bản trên là:
Đáp án đúng là: B
Đọc khái quát, suy luận, loại trừ
Đáp án cần chọn là: B
Việc phản hồi không an toàn của các Chatbox AI tới đối tượng trẻ em là do nguyên nhân nào?
Đáp án đúng là: A
Căn cứ vào đoạn 4
Đáp án cần chọn là: A
Theo đoạn 1 - Các nhà phát triển công nghệ trí tuệ nhân tạo đang thiếu quan tâm đến việc đảm bảo an toàn cho trẻ em khi sử dụng công nghệ AI.
Đúng hay sai
Đáp án đúng là: B
Căn cứ vào đoạn 1.
Đáp án cần chọn là: B
Đoạn văn số 2 sử dụng thao tác lập luận nào?
Đáp án đúng là: B
Căn cứ vào đoạn văn số 2, đọc hiểu
Đáp án cần chọn là: B
Nguyên nhân nào dẫn đến sự cố phản hồi nguy hiểm của trợ lý giọng nói AI của Amazon với một em bé 10 tuổi năm 2021?
Đáp án đúng là: A
Căn cứ vào đoạn văn số 2
Đáp án cần chọn là: A
Hãy hoàn thành các câu sau bằng cách kéo thả các từ vào đúng vị trí:
Việc bảo đảm an toàn cho trẻ em khi sử dụng AI không chỉ là của các công ty công nghệ mà còn cần của toàn xã hội. Bằng cách áp dụng những biện pháp chủ động và hợp lý, chúng ta có thể bảo vệ trẻ em khỏi những tiềm ẩn và giúp chúng tận dụng tối đa lợi ích từ công nghệ mới mẻ này.
Đáp án đúng là: Nghĩa vụ; Sự chung tay; Hiểm hoạ
Đọc hiểu, nghĩa của từ
Đáp án cần chọn là: Nghĩa vụ; Sự chung tay; Hiểm hoạ
Hãy tìm một cụm từ không quá bốn tiếng trong văn bản để hoàn thành nhận định sau:
Nhiều hệ thống trí tuệ nhân tạo đang hiển thị các thông tin không thật sự chính xác, không có sự kiểm chứng xác thực, hay cung cấp giải pháp tiêu cực là do _________ nội dung hiệu quả.
Đáp án đúng là: thiếu kiểm soát
Dựa vào đoạn 5
Đáp án cần điền là: thiếu kiểm soát
TS. Nomisha Kurian từ Đại học Cambridge cho rằng: Trẻ em không phải là đối tượng của các nhà phát triển công nghệ AI trong các lĩnh vực đời sống.
Đúng hay sai
Đáp án đúng là: B
Dựa vào đoạn số 3
Đáp án cần chọn là: B
Dựa vào đoạn văn số 4 trả lời câu hỏi sau: Sự khác biệt giữa trẻ em và người lớn trong việc sử dụng chatbox AI là:
Đáp án đúng là: D
Căn cứ vào đoạn văn số 4
Đáp án cần chọn là: D
Hãy tìm một cụm từ không quá bốn tiếng trong văn bản để hoàn thành nhận định sau:
AI có thể tạo ra các nội dung mới mẻ, chỉ cần gõ câu hỏi, gõ yêu cầu và AI sẽ đáp ứng, điều này có thể tác động xấu đến tâm lý hành vi, có thể làm hạn chế ________________.
Đáp án đúng là: Tư duy sáng tạo
Căn cứ vào đoạn văn số 5
Đáp án cần điền là: Tư duy sáng tạo
Đọc văn bản sau và trả lời các câu hỏi từ 11 đến 20:
MỘT CƠN GIẬN
[Tóm lược đoạn trước: Nhân vật tôi – Anh Thanh gọi một chiếc xe xích lô chở mình “về gần nhà bò Yên Phụ” và mặc cả với giá “bốn xu” trong khi người phu xe “co ro vì rét”, “đã có tuổi” xin sáu xu. Điều đó khiến nhân vật tôi càng thêm bực tức. Anh xe này đã vào đây kéo trộm, vì xe ngoại ô không được phép vào thành phố đón khách, nếu không tuân lệnh thì bị phạt từ ba đến bốn đồng bạc. Khi bị cảnh sát Tây hỏi, anh Thanh vốn đã khó chịu vì sự tồi tàn của cái xe lại thêm sự van nài của anh lái xe, đã trả lời bằng tiếng Pháp với cảnh sát Tây là xe đi trong nội thành “từ Hàng Bún” nên rắc rối đã xảy đến với anh phu xe]
[1]… Những ngày hôm sau thực là những ngày khổ cho tôi. Lòng hối hận không để tôi yên. Hình như có một cái gì nặng nề đè nén trên ngực làm cho tôi khó thở, và lúc nào hình ảnh anh phu xe cũng hiển hiện ra trước mắt.
[2] Tôi nhất định đem tiền đến cho người xe kia để chuộc tội lỗi của mình. Đến phố hàng Bột hỏi dò những người chung quanh xưởng xe, tôi biết được anh xe bị phạt đêm hôm ấy là tên Dư, và ở trong một dãy nhà quá ngã tư Khâm Thiên.
[3] Lần ấy là lần đầu tôi bước vào một chỗ nghèo nàn, khổ sở như thế. Các anh thử tưởng tượng một dãy nhà lụp xụp và thấp lè tè, xiêu vẹo trên bờ một cái đầm mà nước đen và hôi hám tràn cả vào đến thềm nhà. Trong cái hang tối tăm bẩn thỉu ấy, sống một đời khốn nạn những người gầy gò, rách rưới như những người trong một cơn mê.
[...]
[4] Tôi gật đầu ra hiệu cho bà cụ cứ nói:
- Hôm ấy cai nó phải đem tiền lên nộp phạt để chuộc xe về. Chú nó đã xin khất với cai để rồi trả dần số tiền đó. Nhưng nó nhất định không nghe, bắt phải trả một nửa ngay. Khốn nạn, thì lấy đâu ra mà trả. Thế là bị nó lột quần áo đánh một trận thừa sống thiếu chết thầy ạ. Khi về đây lê đi không đuợc nữa. Thế mà nó còn bắt mai phải trả ngay.
Người đàn bà ngồi trong cất tiếng ốm yếu nói theo:
- Nó còn bảo hễ không trả nó sẽ bắt lấy thẻ.
- Thế bây giờ bác ta đâu?
Bà cụ trả lời:
- Đi ngay từ hôm ấy, mà không biết đi đâu. Đã ba hôm nay chúng tôi dò mà không thấy. Chắc là sợ cai không dám về nữa, dù có về mà không có tiền cũng chết với nó. Thật cũng là cái vạ, nghe đâu chú nó nói hôm ấy tại người khách đi xe không biết nói với người đội xếp thế nào mới bị bắt, chứ không cũng chẳng việc gì.
Tôi yên lặng, trong lòng náo nức.
Bà cụ chép miệng, chỉ người đàn bà ngồi sau:
- Tội cho vợ con chú đây, ốm đã mấy ngày hôm nay không có thuốc. Đứa cháu không biết có qua khỏi được không?
Tôi đứng lại gần xem. Trên cánh tay người mẹ, chỉ còn là một dúm thịt con đã nhăn nheo: đứa bé há hốc miệng thở ra, mặt xám nhợt. Người mẹ thỉnh thoảng lấy cái lông gà dúng vào chén mật ong để bên cạnh, phết lên lưỡi của đứa bé.
- Cháu nó sài đã hơn một tháng nay. Hôm nọ đã đỡ. Mấy hôm nay vì không có tiền mua thuốc lại tăng. Ông lang bảo cháu khó qua khỏi được.
Người mẹ nói xong nấc lên một tiếng rồi nức nở khóc. Bà cụ già lê nhích lại gần, cúi xuống khe khẽ kéo lại những cái tã rách như xơ mướp.
[5] Cái cảnh đau thương ấy làm tôi rơm rớm nước mắt. Một cảm giác nghẹn ngào đưa lên chẹn lấy cổ. Tôi lấy tờ giấy bạc năm đồng đưa cho người mẹ, rồi vội vàng bước ra cửa, để mặc hai người nhìn theo ngờ vực.
[6] Qua ngưỡng cửa, tôi va phải một người đàn ông ốm yếu tay cắp một cái áo quan con bằng gỗ mới. Đến bên đường, tôi nghe thấy trong căn nhà lụp xụp đưa ra tiếng khóc của hai người đàn bà.
Đứa bé con đã chết.
[7] Anh Thanh lặng yên một lát như nghĩ ngợi, rồi nói tiếp:
- Cái kỷ niệm buồn rầu ấy cứ theo đuổi tôi mãi mãi đến bây giờ, rõ rệt như các việc mới xảy ra hôm qua. Sự đó nhắc cho tôi nhớ rằng người ta có thể tàn ác một cách dễ dàng. Và mỗi lần tôi nghĩ đến anh phu xe ngoại ô kia, lại thấy đau đớn trong lòng, như có một vết thương chưa khỏi.
(Thạch Lam, “Tuyển tập Thạch Lam”, NXB Văn học, 2018)
Trả lời cho các câu 51, 52, 53, 54, 55, 56, 57, 58, 59, 60 dưới đây:
Lý do nhân vật tôi lòng hối hận không yên là vì chưa đem tiền đến cho người xe kia để chuộc tội lỗi của mình.
Đúng hay sai?
Đáp án đúng là: B
Căn cứ phần tóm tắt
Đáp án cần chọn là: B
Nhận xét giọng văn thể hiện trong đoạn trích:
Đáp án đúng là: A
Đọc hiểu, sự hiểu biết của bản thân về tác giả Thạch Lam
Đáp án cần chọn là: A
Hãy điền một từ/ cụm từ không quá hai tiếng vào chỗ trống để hoàn thành nhận định sau.
Câu văn “Trong cái hang tối tăm bẩn thỉu ấy, sống một đời khốn nạn những người gầy gò, rách rưới như những người trong một cơn mê” là 1 câu văn độc đáo, bởi chỉ với hai dòng, nhà văn đã sử dụng đến 3 biện pháp nghệ thuật: so sánh, liệt kê, __________ để làm bật lên hình ảnh cuộc sống khốn khổ của những kiếp người sống dưới đáy xã hội.
Đáp án đúng là: Đảo ngữ
Nhận diện, Kiến thức tiếng Việt
Đáp án cần điền là: Đảo ngữ
Nhận xét sau đây đúng hay sai:
Truyện ngắn Một cơn giận đã thể hiện sâu sắc giá trị nhân đạo ở chỗ: Phản ánh thế lực của cường quyền, tiền quyền đẩy những con người khốn khổ đến bước đường cùng.
Đáp án đúng là: B
Đọc hiểu, nhận biết
Đáp án cần chọn là: B
Phương thức biểu đạt chính của đoạn 1 là:
Đáp án đúng là: B
Đọc hiểu, nhận biết đoạn 1
Đáp án cần chọn là: B
Vì sao bà cụ và người mẹ của anh phu lại ngờ vực trước việc nhân vật tôi đưa tờ giấy bạc năm đồng cho họ? (chọn nhiều đáp án)
Đáp án đúng là: A; B
Đọc hiểu, suy luận
Đáp án cần chọn là: A; B
Bệnh sài (chữ in đậm) được đề cập đến trong văn bản là bệnh gì? (chọn hai phương án)
Đáp án đúng là: B; C
Đọc kĩ yêu cầu của đề bài đối chiếu với bài đọc.
Đáp án cần chọn là: B; C
Từ “náo nức” trong đoạn số 4 thể hiện ý nghĩa gì?
Đáp án đúng là: C
Giải nghĩa của từ
Đáp án cần chọn là: C
Bài học nào KHÔNG phải thông điệp mà tác phẩm đề cập
Đáp án đúng là: A
Dựa vào đọc hiểu toàn văn bản
Đáp án cần chọn là: A
Hãy hoàn thành các câu sau bằng cách kéo thả các từ vào đúng vị trí:
Tính cách và dễ bực tức của Thanh đã gây ra những hậu quả cho cuộc sống của anh, làm anh phải hối hận sau đó. Điều này phản ánh một phần tâm lý con người khi không kiểm soát được cảm xúc, dẫn đến những hành động cho bản thân và người khác.
Đáp án đúng là: Nóng nảy; Tai hại; Trầm trọng
Đọc thật kĩ yêu cầu của đề bài, đối chiếu với đoạn văn, suy luận, tổng hợp.
Đáp án cần chọn là: Nóng nảy; Tai hại; Trầm trọng
Phần 3: Tư duy khoa học/Giải quyết vấn đề
Đọc đoạn thông tin sau và trả lời từ câu 1 đến câu 5:
Sóng cơ là dao động cơ lan truyền trong một môi trường. Các đại lượng đặc trưng của chuyển động sóng bao gồm chu kì $(T)$, tần số sóng $(f)$, biên độ sóng $(A)$, bước sóng $(\lambda)$, tốc độ truyền sóng $(v)$ và năng lượng sóng. Bước sóng là quãng đường mà sóng truyền được trong một chu kì:
$\lambda = v \cdot T = \dfrac{v}{f}(1)$
Tốc độ truyền sóng cơ phụ thuộc vào mật độ phần tử của môi trường truyền sóng: mật độ phần tử môi trường truyền sóng càng lớn thì sóng cơ truyền càng nhanh và ngược lại. Khi hai sóng cùng phương, cùng tần số và có hiệu số pha không đổi theo thời gian (hai sóng kết hợp) gặp nhau thì trong vùng gặp nhau của hai sóng xuất hiện những điểm mà ở đó phần tử môi trường dao động với biên độ cực đại và những điểm mà ở đó phần từ môi trường dao động với biên độ cực tiểu. Hiện tượng này được gọi là hiện tượng giao thoa sóng.
Khi gặp vật cản, sóng cơ bị phản xạ. Sóng phản xạ và sóng tới có cùng bước sóng và tần số. Sóng tới và sóng phản xạ nếu truyền trên cùng một phương thì có thể giao thoa với nhau tạo thành hệ sóng dừng với các điểm bụng (phần tử môi trường dao động với biên độ cực đại) và điểm nút (phần tử môi trường đứng yên) cố định. Điều kiện để có sóng dừng trên sợi dây đàn hồi có chiều dài $\mathcal{l}(m)$ hai đầu cố định là:
$\mathcal{l} = k \cdot \dfrac{\lambda}{2}(2)$ với k là số bụng sóng
Để nghiên cứu sóng dừng trên một sợi dây dài đàn hồi, một học sinh tiến hành thí nghiệm:
* Bố trí thí nghiệm: Một đầu của sợi dây được gẳn với cần rung của một máy phát dao động với tần số f , đầu còn lại treo vật có khối lượng M vắt qua một ròng rọc cố định (Hình 1).
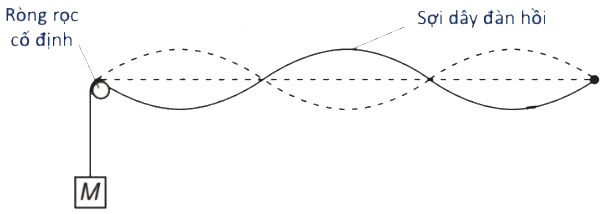
Hình 1
* Tiến hành thí nghiệm:
- Điều chỉnh khối lượng $M$ của vật treo cho tới khi trên dây xuất hiện sóng dừng với $k$ bụng sóng.
- Lặp lại thí nghiệm với khối lượng $M$ khác nhau để thu được các giá trị khác nhau của $k$. Kết quả thí nghiệm cho bởi Bảng 1 .
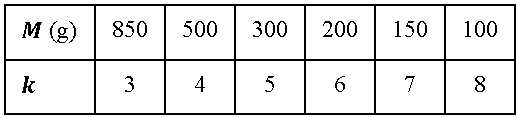
Bảng 1. Kết quả thi nghiệm
Biết rằng, mỗi giá trị của $M$ trong Bảng 2 có sai số $10\%$.
Mối liên hệ giữa $M$ và $k$ được cho bởi công thức: $f = \dfrac{k}{2\mathcal{l}}\sqrt{\dfrac{Mg}{\mu}}$ (3)
trong đó: $f(Hz)$ là tần số sóng trên dây, $g\left( {m/s^{2}} \right)$ là gia tốc rơi tự do tại nơi làm thí nghiệm $\mu(g/m)$ là khối lượng trên một đơn vị chiều dài của sợi dây.
(Soạn dựa theo nội dung sách giáo khoa Vật lí 12 và số liệu thực nghiệm)
Trả lời cho các câu 61, 62, 63, 64, 65 dưới đây:
Sóng truyền trên một sợi dây đàn hồi với tốc độ $20m/s$ và bước sóng 80 cm . Chu kì sóng là bao nhiêu giây?
Đáp án đúng là: 0,04
Chu kì sóng: \(T = \frac{\lambda }{v}\)
Đáp án cần điền là: 0,04
Trên một sợi dây đàn hồi đang có sóng dừng ổn định. Bụng sóng là các vị trí mà tại đó phần tử của dây dao động với biên độ ...................
Đáp án đúng là: A
Sử dụng lý thuyết sóng dừng
Đáp án cần chọn là: A
Phát biểu dưới đây là đúng hay sai?
Khi một sóng cơ truyền từ không khí vào nước thì tần số sóng không đổi và bước sóng giảm.
Đáp án đúng là: B
Tần số sóng không đổi khi truyền qua các môi trường.
Đáp án cần chọn là: B
Điền số thích hợp vào chỗ trống.
Trong thí nghiệm mà học sinh thực hiện, khi trên dây có 4 bụng sóng thì khối lượng M của vật treo là \( \pm \) (g).
Đáp án đúng là: 500; 50
Sử dụng thông tin từ bảng số liệu 1
Đáp án cần điền là: 500; 50
Trong thí nghiệm mà học sinh thực hiện, khi M giảm đến giá trị lại xuất hiện sóng dừng thì tốc độ truyền song tắng nên số lượng bụng sóng tăng.
Đáp án đúng là: A
Nhìn vào bảng 1, M giảm thì k tăng
Đáp án cần chọn là: A
Điền số thích hợp vào chỗ trống (2 số ngăn cách nhau bởi dấu chấm phẩy)
Trong thí nghiệm mà học sinh thực hiện, khi trên dây có 4 bụng sóng thì khối lượng M của vật treo là.........................![]() \( \pm \) .........................
\( \pm \) ......................... ![]() (g).
(g).
Đáp án đúng là: 500;50
Sử dụng thông tin từ bảng số liệu 1
Đáp án cần điền là: 500;50
Khi chiếu tia laser (sóng điện từ) đến hai khe hẹp, ánh sáng đi qua hai khe này và mỗi khe trở thành một nguồn phát sóng. Lúc này xảy ra hiện tượng giao thoa của sóng phát ra từ hai khe. Ta có thể giải thích hiện tượng này giống như khi giải thích hiện tượng giao thoa sóng mặt nước.
Để trực quan hơn, ta sử dụng hình ảnh sau: trong đó vẽ các mặt đầu sóng đều là đỉnh sóng, khoảng cách giữa hai mặt đầu sóng chính là bước sóng.
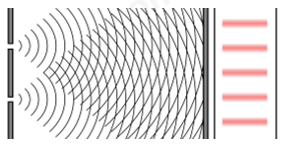
Những vị trí trên màn mà ở đó sóng từ hai nguồn tăng cường lẫn nhau thì cường độ sáng tại vị trí đó lớn, xuất hiện vệt sáng gọi là vân sáng.
Những vị trí trên màn mà ở đó sóng từ hai nguồn triệt tiêu lẫn nhau thì cường độ sáng tại vị trí đó nhỏ (theo lí thuyết là bằng không), vùng đó không được chiếu sáng từ hai nguồn nên gọi là vân tối.
Khoảng cách giữa hai vân sáng liên tiếp (hoặc hai vân tối liên tiếp) gọi là khoảng vân.
Từ lí thuyết giao thoa, ta rút ra được khoảng vân $i$ (khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp) liên hệ với khoảng cách giữa hai khe $a$, khoảng cách giữa hai khe với màn quan sát $D$ và bước sóng ánh sáng $\lambda$ theo công thức:
$i = \dfrac{\lambda D}{a}$
Trong bài thực hành này, chúng ta sử dụng Bộ thí nghiệm xác định bước sóng ánh sáng (như hình 1). Bộ thí nghiệm này gồm có:
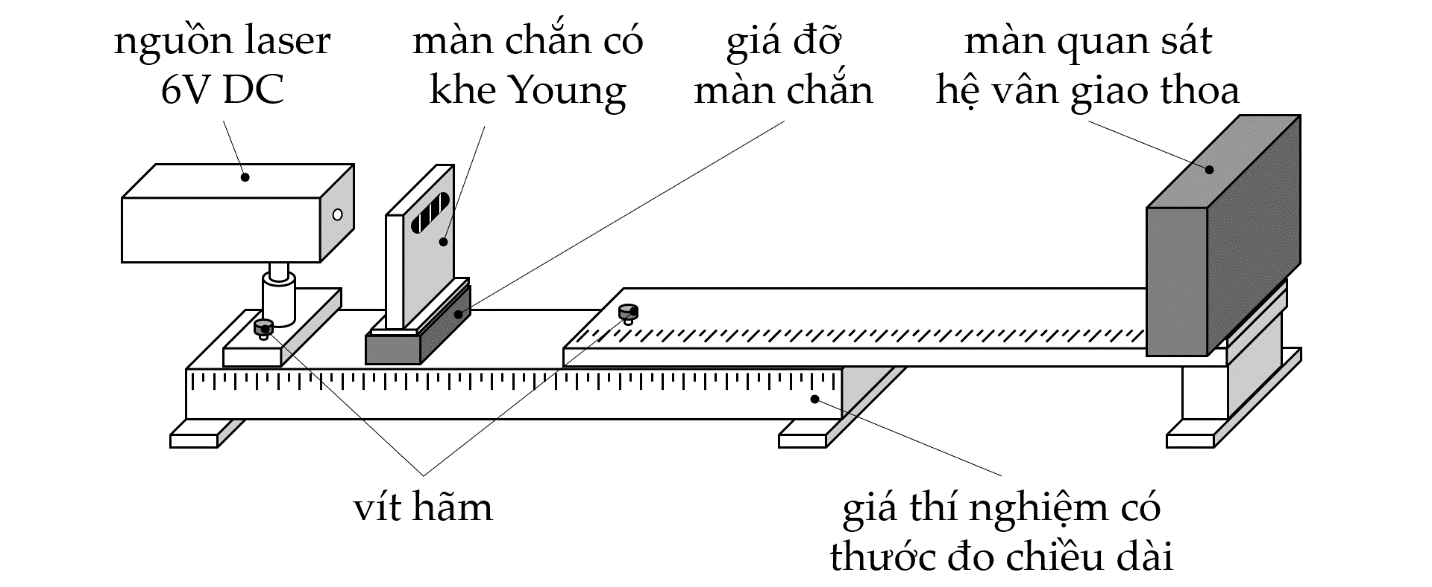
Hình 1: Bố trí thí nghiệm đo bước sóng ánh sáng
(1) Giá thí nghiệm có thước đo chiều dài, có thể thay đổi được chiều dài và cố định chiều dài bằng vít hãm.
(2) Nguồn laser sử dụng điện áp một chiều 6V.
(3) Màn chắn có khe Young
(4) Màn quan sát hệ vân giao thoa. Trên màn có thước đo với độ chia nhỏ nhất $1~mm$.
(5) Nguồn điện.
Nguồn laser:
Hiệu điện thế định mức của nguồn laser là 6V DC. Cần chú ý cấp đúng định mức để thiết bị hoạt động bình thường.
Nguồn laser phát ra ánh sáng trong vùng bước sóng đỏ, có cường độ cao. Vì vậy khi sử dụng tuyệt đối không chiếu vào mắt. Nên dùng một vật che đầu phát của laser trước khi cấp điện, để tránh hiện tượng chiếu nhầm vào mắt của mình và mọi người xung quanh.
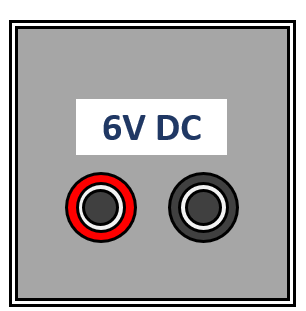
Khe Young:
Trên màn chắn có khe Young là 3 cặp khe, khoảng cách lần lượt giữa các cặp khe này là $mm;0,15~mm$ và $mm$. Gắn gắn màn chắn này lên giá đỡ màn chắn rồi gắn lên giá thí nghiệm, ta có thể trượt màn qua lại theo phương ngang để thay đổi khe Young khi làm thí nghiệm.
Hãy điều chỉnh khe Young sao cho hệ vân trên màn quan sát hiện lên rõ nhất, từ đó thuận tiện cho việc đo đạc.
Màn quan sát:
Màn quan sát dùng để hứng hệ vân giao thoa. Trên màn có chứa 2 thước theo phương ngang với độ chia nhỏ nhất lần lượt là 5 mm và 1 mm.
Tương tự như màn chứa khe Young, ta có thể trượt màn quan sát để vân giao thoa nằm ở vị trí dễ đọc, từ đó dễ đo được giá trị khoảng vân.
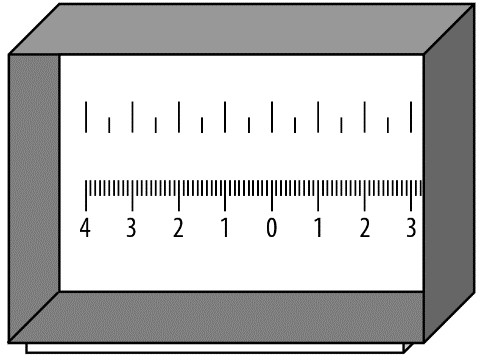
Thí nghiệm 1: Cố định a = 0,15 mm và thay đổi D
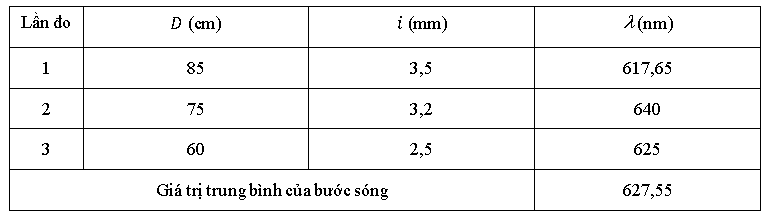
Thí nghiệm 2: Cố định D = 80 cm và thay đổi a
Trả lời cho các câu 67, 68, 69, 70, 71, 72, 73, 74, 75 dưới đây:
Em hãy đánh giá đúng/sai cho các nhận xét sau:
| Đúng | Sai | |
|---|---|---|
| a) Vị trí trên màn mà ở đó sóng từ hai nguồn tăng cường lẫn nhau thì sẽ xuất hiện vân sáng. | ||
| b) Khoảng cách giữa 3 vân sáng hoặc 2 vân tối liên tiếp gọi là khoảng vân. | ||
| c) 6V DC nghĩa là hiệu điện thế định mức một chiều 6V. | ||
| d) Có 3 cặp khe Young trong thí nghiệm lần lượt là $0,1~mm$; $0,2~mm$ và $0,3~mm$. |
Đáp án đúng là: Đ; S; Đ; S
Sử dụng lý thuyết giao thoa sóng
Đáp án cần chọn là: Đ; S; Đ; S
Em hãy sắp xếp các hoạt động thí nghiệm sau để hoàn thiện bảng số liệu trong quá trình đo bước sóng? Điền số thích hợp vào chỗ trống (Đảm bảo tính logic)
1- Bố trí thí nghiệm như hình 1.
2- Viết kết quả đo được.
3- Xác định khoảng cách giữa 2 khe trong thí nghiệm, đo nhiều lần khoảng cách từ 2 khe đến màn và đo khoảng cách giữa 2 vân sáng.
4- Tính sai số của bước sóng.
5- Tính giá trị trung bình của bước sóng.
Thứ tự đúng sẽ là ___-___-___-___-___
Đáp án đúng là: A
Sử dụng lý thuyết thực hành giao thoa ánh sáng
Đáp án cần chọn là: A
Chọn đáp án đúng:
Cố định khoảng cách giữa màn quan sát và hai khe. Lần lượt sử dụng khe 0,1 mm; 0,15 mm và 0,2 mm. Khoảng vân thay đổi như thế nào?
Đáp án đúng là: B
Khoảng vân: \(i = \frac{{\lambda D}}{a}\)
Đáp án cần chọn là: B
Trong thí nghiệm Y-âng về giao thoa ánh sáng, hai khe được chiếu bằng ánh sáng laze đỏ. Nếu tại điểm M trên màn quan sát gần vân trung tâm nhất là vân sáng thì hiệu đường đi của ánh sáng từ hai khe S1, S2 đến M bằng bao nhiêu lần bước sóng?
Đáp án đúng là: 1
Tại vị trí vân sáng có hiệu đường đi của ánh sáng giữa hai khe: \({d_2} - {d_1} = k\lambda \)
Đáp án cần điền là: 1
Trong thí nghiệm I - âng về giao thoa ánh sáng, hai khe được chiếu bằng ánh sáng đỏ có bước sóng λ. Nếu tại điểm M trên màn quan sát có vân tối thứ hai (tính từ vân sáng trung tâm) thì hiệu đường đi của ánh sáng từ hai khe S1, S2 đến M có độ lớn bằng bao nhiêu lần bước sóng?
Đáp án đúng là: 1,5
Tại vị trí vân tối có hiệu đường đi của ánh sáng giữa hai khe: \({d_2} - {d_1} = \left( {k + \frac{1}{2}} \right)\lambda \)
Đáp án cần điền là: 1,5
Trong thí nghiệm 1 ở lần đo 2, bước sóng có độ dài là bao nhiêu nm?
Đáp án đúng là: 640
Sử dụng thông tin từ bảng số liệu của thí nghiệm 1
Đáp án cần điền là: 640
Giá trị trung bình của bước sóng sau 2 thí nghiệm là bao nhiêu nm?
Đáp án đúng là: 631,44
Sử dụng thông tin từ bảng số liệu thí nghiệm 2
Đáp án cần điền là: 631,44
Trong thí nghiệm 2, sai số của bước sóng trung bình khoảng bao nhiêu %?
Đáp án đúng là: 2,17
Sai số tỉ đối: \(\delta \lambda = \frac{{\overline {\Delta \lambda } }}{{\overline \lambda }}\)
Đáp án cần điền là: 2,17
Trong thí nghiệm Y-âng về giao thoa ánh sáng ở trên, hai khe được chiếu bằng ánh sáng laze đỏ có bước sóng 0,6 μm. Khoảng cách giữa hai khe là 1 mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 1,2 m, bề rộng miền giao thoa là 1,25 cm.
a) Tổng số vân sáng có trong miền giao thoa là bao nhiêu vân?
b) Tổng số vân tối có trong miền giao thoa là bao nhiêu vân?
(Hai đáp án ngăn cách nhau bởi dấu chấm phẩy).
Đáp án đúng là: 17;18
Khoảng vân: \(i = \frac{{\lambda D}}{a}\)
Số vân sáng: \({n_s} = 2.\left[ {\frac{L}{{2i}}} \right] + 1\)
Số vân tối: \({n_t} = 2.\left[ {\frac{L}{{2i}} + \frac{1}{2}} \right]\)
Đáp án cần điền là: 17;18
ĐIỆN PHÂN DUNG DỊCH
Điện phân là quá trình oxi hóa – khử xảy ra trên bề mặt các điện cực dưới tác dụng của dòng điện một chiều đi qua trong dung dịch chất điện li hoặc chất điện li nóng chảy. Ở quá trình điện phân của các ion trong nước, các ion sẽ di chuyển về phía điện cực mang điện tích trái dấu với nó. Các ion kim loại kiềm, kiềm thổ (Na+, K+, Ca2+…) và gốc muối có chứa oxygen (NO3-, CO32-,…) không tham gia quá trình điện phân mà nước sẽ bị điện phân. Tại điện cực dương (anode), xảy ra quá trình oxi hoá với sự nhường electron của chất có tính khử mạnh hơn, trong khi đó tại điện cực âm (cathode), xảy ra quá trình khử với sự nhận electron của chất có tính oxi hoá mạnh hơn.
Ví dụ quá trình điện phân nước ở mỗi điện cực
Anode: 2H2O ⟶ O2 + 4H+ + 4e
Cathode: 2H2O + 2e ⟶ H2 + 2OH-
Một trong những ứng dụng của phương pháp điện phân là mạ điện - đó là quá trình phủ một lớp kim loại lên bề mặt kim loại khác. Trong quá trình mạ điện, vật cần mạ được gắn với điện cực âm, kim loại mạ là một thanh nguyên chất được gắn với cực dương và cùng nhúng trong dung dịch chứa ion kim loại cần mạ. Khi có dòng điện chạy qua, các ion kim loại di chuyển về cực âm, bị khử thành kim loại và phủ lên vật cần mạ. Trên thực tế, để thu được lớp mạ sáng bóng, có độ bám tốt thì còn phải chú ý nhiều yếu tố khác như pH, nhiệt độ, cũng như thành phần và nồng độ các chất trong dung dịch.
Trả lời cho các câu 76, 77, 78, 79, 80, 81 dưới đây:
Những phát biểu nào dưới đây là đúng?
Khi điện phân dung dịch NaCl có màng ngăn thì
Đáp án đúng là: A; B; C
Đọc đoạn văn và trả lời câu hỏi.
Đáp án cần chọn là: A; B; C
Điền từ/cụm từ thích hợp vào chỗ trống?
Các vật làm bằng nhôm thường khá bền do có lớp màng oxide Al2O3 khó bị ăn mòn bởi các tác nhân oxi hoá. Người ta có thể tạo ra lớp oxide đó bằng phương pháp điện phân dung dịch acid với một điện cực làm bằng vật dụng nhôm cần tạo lớp màng oxide. Khi đó nhôm sẽ phản ứng với khí oxygen sinh ra ở điện cực nhờ quá trình điện phân nước. Vật dụng bằng nhôm được nối với điện cựccủa dòng điện một chiều. Tại bề mặt nhôm xảy ra quá trình .
Đáp án đúng là: dương; oxi hóa
Nguyên tắc điện phân:
(-) Cathode: xảy ra quá trình khử
(+) Anode: xảy ra quá tình oxi hóa
Đáp án cần chọn là: dương; oxi hóa
Người ta có thể tách các cation kim loại ra khỏi dung dịch bằng cách điện phân phân đoạn (điện phân khống chế hiệu điện thế áp đặt vào hai cực), khi đó cation có tính oxi hoá lớn hơn sẽ bị điện phân trước và tách nước ra. Điện phân phân đoạn (với điện cực trơ) dung dịch chứa các ion Ag+, Cu2+, Ni2+ và Mg2+ với anion $NO_{3}^{-}$. Cation nào sẽ bị điện phân trước tại cathode?
Đáp án đúng là: D
Căn cứ vào dữ liệu đoạn văn:’’cation có tính oxi hoá lớn hơn sẽ bị điện phân trước và tách nước ra’’.
Đáp án cần chọn là: D
Nhận định dưới đây là đúng hay sai?
‘’Trong sản xuất vỏ hộp, người ta có thể tráng thiếc (Sn) lên bề mặt thép bằng phương pháp điện phân với anode làm bằng Sn và cathode là vật làm bằng thép cần được mạ’’
Đáp án đúng là: A
Nguyên tắc mạ điện:
Quá trình xảy ra trong bình điện phân:
Anode (+): xảy ra quá trình oxi hóa
Cathode (-): xảy ra quá trình khử
Đáp án cần chọn là: A
Kéo thả cụm từ thích hợp vào chỗ trống?
Trong quá trình mạ điện, khối lượng cathode, khối lượng anode.
Đáp án đúng là: tăng lên; giảm xuống
Căn cứ vào dữ liệu đoạn văn.
Đáp án cần chọn là: tăng lên; giảm xuống
Người ta muốn mạ nickel lên một vật X có có diện tích 100 cm2, độ dày của lớp nikel phủ đều trên bề mặt là a μm. Dòng điện chạy qua bình điện phân có cường độ 0,5 A và thời gian mạ là 5 giờ. Giá trị của a là bao nhiêu? (Kết quả làm tròn đến hàng phần mười). Biết nikel có khối lượng mol nguyên tử là 58,7 g/mol; hoá trị II; khối lượng riêng là 8,8.103 kg/m3 và số mol nikel bám vào bề mặt vật X được tính theo công thức n =$\dfrac{I.t}{N.F}$
Trong đó:
t là thời gian điện phân (giây).
n là số mol chất sinh ra ở điện cực (mol).
N là số electron trao đổi.
F là hằng số Faraday (F = 96500).
I là cường độ dòng điện (A).
Đáp án đúng là: 31,1
Áp dụng công thức nNi =\(\dfrac{{I.t}}{{N.F}}\)
Đáp án cần điền là: 31,1
CITRULLINE
L – citrulline là một α – amino acid không thiết yếu có thể được tổng hợp trong cơ thể từ các hợp chất khác. L – citrulline có khả năng giảm đau mỏi cơ, tăng sức bền vận động và cải thiện chức năng sinh lí nam. Loại amino acid này được bổ sung vào đồ uống sinh dưỡng thể thao và được xem là một loại thực phẩm chức năng dạng viên hay bột.
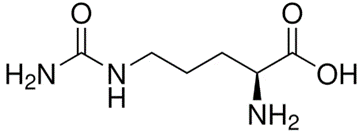
L – citrulline
Dưa hấu là một loại trái cây giàu L – citrulline. Phương pháp quang phổ hấp thụ UV-Vis được sử dụng để xác định hàm lượng L – citrulline trong vỏ trắng và thịt quả của dưa hấu dựa trên sự hình thành hợp chất màu (độ hấp thụ cực đại ở 490 nm đối với citrulline) do phản ứng của L – citrulline với diacetyl monoxime trong môi trường acid. Ánh sáng của bước sóng chiếu vào hỗn hợp phản ứng. Độ hấp thụ ánh sáng của hỗn hợp phản ứng sẽ được thiết bị đo được và giá trị này tỉ lệ thuận với nồng độ L – citrulline trong một phạm vi nhất định.
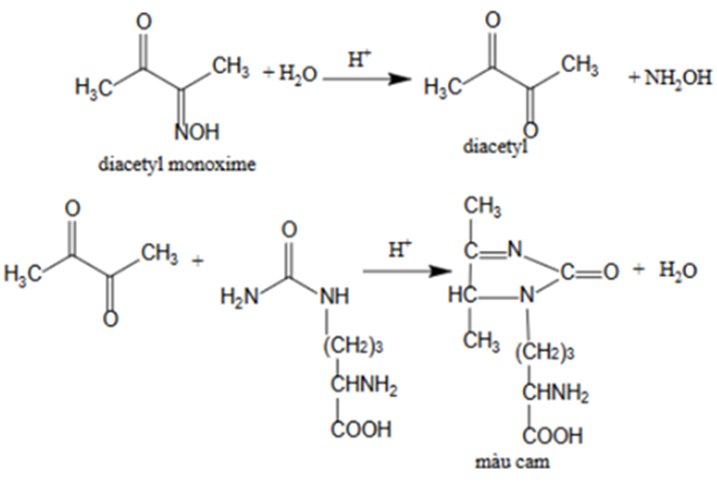
Phản ứng tạo hợp chất màu của L - citrulline với diacetyl monoxime
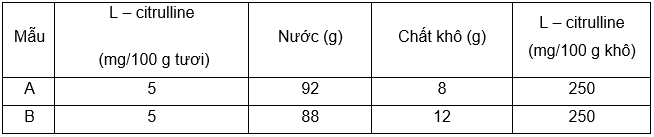
Tiến hành phân tích hàm lượng L – citrulline có trong vỏ trắng, thịt quả của dưa hấu ở 4 địa điểm khác nhau bằng phương pháp quang phổ hấp thụ UV-Vis từ hàm lượng L – citrulline được quy đổi theo trọng lượng khô, thu được kết quả như hình 1:
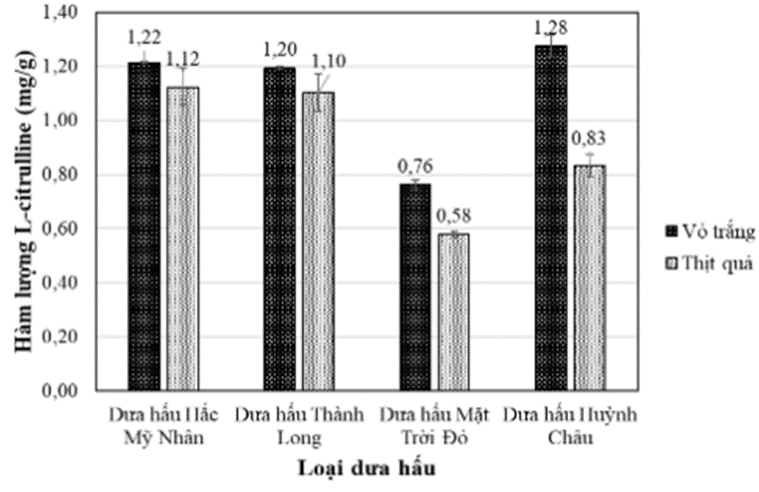
Hình 1: Hàm lượng L – Citrulline phân bố trong các loại dưa hấu khác nhau
Trả lời cho các câu 82, 83, 84, 85, 86, 87, 88 dưới đây:
Công thức phân tử của L - citrulline là
Đáp án đúng là: A
Từ CTCT để suy ra CTPT.
Đáp án cần chọn là: A
Những phát biểu nào sau đây là đúng về L – citrulline?
Đáp án đúng là: A; B; E
Từ CTCT để suy ra tính chất.
Căn cứ vào dữ liệu đoạn văn.
Đáp án cần chọn là: A; B; E
Phát biểu dưới đây là đúng hay sai?
| Đúng | Sai | |
|---|---|---|
| a) L - citrulline phản ứng với với diacetyl monoxime được thực hiện trong môi trường acid. | ||
| b) Nồng độ L – citrulline càng lớn thì độ hấp thụ càng giảm. | ||
| c) Số nguyên tử hydrogen trong hợp chất màu cam là 17. | ||
| d) Hợp chất màu cam là hợp chất có chứa vòng. |
Đáp án đúng là: Đ; S; Đ; Đ
Căn cứ vào phản ứng tạo hợp chất màu của L - citrulline với diacetyl monoxime.
Đáp án cần chọn là: Đ; S; Đ; Đ
Hàm lượng L – citrulline có trong thịt quả ở 4 địa điểm tính theo trọng lượng khô dao động từ
Đáp án đúng là: B
Phân tích dữ liệu hình 1.
Đáp án cần chọn là: B
Kéo thả từ/cụm từ thích hợp vào chỗ trống?
’Hàm lượng L – citrulline phân bốtrong quả dưa hấu, trong đó vỏ trắng chứathịt quả của các loại dưa hấu khác nhau.’’
Đáp án đúng là: khác nhau; nhiều hơn
Phân tích dữ liệu hình 1.
Đáp án cần chọn là: khác nhau; nhiều hơn
Để sản xuất được 100 hộp thuốc có chứa L – citrulline thì cần bao nhiêu tấn vỏ trắng khô của dưa hấu Hắc Mỹ Nhân. Biết hàm lượng L – citrulline có trong 1 viên thuốc là 1200 mg. Mỗi hộp thuốc chứa 120 viên? (Làm tròn kết quả đến hàng phần mười)
Đáp án đúng là: 11,8
Phân tích dữ liệu đề bài.
Đáp án cần điền là: 11,8
Nhận định dưới đây là đúng hay sai?
‘’ Khi so sánh hàm lượng L – citrulline giữa các mẫu dưa hấu, nếu không quy đổi theo trọng lượng khô thì có thể dẫn đến kết kết quả sau lệch do ảnh hưởng của lượng nước trong mẫu’’
Đáp án đúng là: A
Phân tích căn cứ vào dữ liệu kết hợp với kiến thức thực tế.
Đáp án cần chọn là: A
Đọc đoạn thông tin sau và trả lời 6 câu hỏi tiếp theo:
SỰ “DI CƯ” CỦA THỰC VẬT
Nhiệt độ và độ ẩm là những nhân tố quan trọng nhất giới hạn sự phân bố địa lý của các loài thực vật và động vật thì sự thay đổi khi hậu trên phạm vi toàn cầu đang diễn ra hiện nay sẽ có ảnh hưởng sâu sắc tới toàn bộ sinh quyển. Có thể nghĩ rằng, sẽ là không phù hợp khi cho rằng thực vật có khả năng “di cư" tuy nhiên hoá thạch về bào tử phấn hoa tìm thấy trong các ao hồ là bằng chứng trực tiếp về sự di cư của thực vật.
Nếu như các nhà khoa học có thể xác định khí hậu giới hạn sự phân bố địa lý hiện tại của các loài, thì họ cũng có thể dự báo sự phân bố đó sẽ thay đổi như thế nào khi nhiệt độ Trái Đất ấm lên. Câu hỏi chủ yếu đặt ra đối với thực vật là liệu phát tán hạt có đủ nhanh để đảm bảo sự di cư của mỗi loài kịp với sự thay đổi của khí hậu
Để nghiên cứu ảnh hưởng của biến đổi khí hậu tới sự phân bố của sinh vật trong thế kỉ XXI, người ta đã xây dựng nhiều mô hình sinh thái dự đoán phân bố trong tương lai của các loài cho đến năm 2100 theo hai kịch bản biến đổi khí hậu: nhiệt độ trung bình tăng thêm 4,5°C hoặc 6,5°C so với năm 2000. Khi xây dựng mô hình phân bố của loài sồi (Fagus grandifolia) theo hai kịch bản trên, các nhà khoa học nhận thấy: giới hạn phân bố phía Bắc của quần thể sồi sẽ dịch chuyển 700 đến 900 km lên phía Bắc, còn giới hạn phía Nam cũng bị dịch chuyển. Nếu dự đoán này là tương đối đúng thì mỗi năm cây sồi sẽ di cư dân lên phía bắc 7-9 km theo tốc độ ấm lên của khí hậu Trái Đất. Trên thực tế, từ sau kỉ băng hà cuối cùng cho đến nay, tốc độ di cư của quần thể sồi chỉ đạt 0,2 km/năm lên phía Bắc do sự ấm lên toàn cầu (nếu như không có tác động của con người trong việc di nhập của loài cây này)
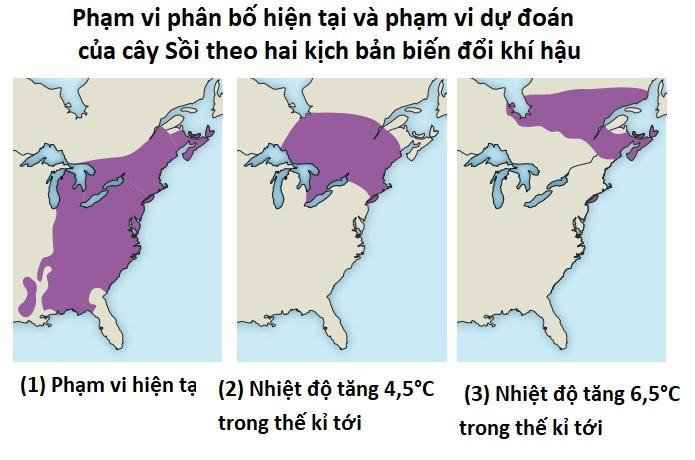
Trả lời cho các câu 89, 90, 91, 92, 93, 94 dưới đây:
Kéo thả đáp án đã cho vào chỗ trống thích hợp
Nhân tố quan trọng nhất giới hạn sự phân bố địa lý của các loài thực vật và động vật là và . Khi nhiệt độ trái đất tăng, thực vật có khả năng để thích nghi và tồn tại với tốc độ
Đáp án đúng là: nhiệt độ; độ ẩm; di cư; chậm
Đọc thông tin bài đọc để tìm từ khóa thích hợp
Đáp án cần chọn là: nhiệt độ; độ ẩm; di cư; chậm
Nhận định dưới đây là đúng hay sai?
| Đúng | Sai | |
|---|---|---|
| a) Hoá thạch về bào tử phấn hoa tìm thấy trong các ao hồ là bằng chứng gián tiếp cho thấy thực vật có khả năng di cư. | ||
| b) Các kịch bản đặt ra đều dự đoán nhiệt độ trái đất tăng. | ||
| c) Loài sồi sẽ có hướng mở rộng phạm vi phân bố ngược nhau trong hai kịch bản về biến đổi khí hậu. | ||
| d) Tốc độ di cư của loài sồi không kịp với tốc độ gia tăng nhiệt độ của trái đất. |
Đáp án đúng là: Đ; S; Đ
Phân tích từng nhận định (a, b, c, d) bằng cách đối chiếu trực tiếp với các dữ kiện và thông tin đã được nêu trong đoạn văn bản và biểu đồ đi kèm.
Đáp án cần chọn là: Đ; S; Đ
Vì sao khi nhiệt độ trung bình của trái đất tăng, loài sồi có xu hướng dịch chuyển vùng phân bố lên phía Bắc?
Đáp án đúng là: A
Phân tích bài đọc để xác định tính chính xác của mỗi mệnh đề
Cách giải:
A – Đúng. Vì loài sồi thích nghi với nền nhiệt nhất định, khi nhiệt độ trái đất tăng ? nó phải di cư đến vùng có khi hậu mát mẻ hơn (di cư lên phía bắc)
B – Sai. Vì phía Bắc có nhiệt độ thấp hơn, thích hợp với loài sồi hơn.
C – Sai. Vì phía Bắc có nhiệt độ thấp hơn, thích hợp với loài sồi hơn.
D – Sai. Vì loài sồi có khả năng phát tán = có khả năng dịch chuyển các thế hệ sau
Đáp án cần chọn là: A
So sánh tốc độ dịch chuyển giới hạn phân bố phía Nam với giới hạn phân bố phía Bắc của quần thể sồi theo mô hình trên?
Đáp án đúng là: B
Phân tích bài đọc để xác định tính chính xác của mỗi mệnh đề
Đáp án cần chọn là: B
Những dự đoán nào sau đây về diện tích và kích thước quần thể sồi sẽ thay đổi như thế nào nếu nhiệt độ trong thế kỉ XXII tiếp tục tăng tương đương tốc độ tăng nhiệt trong thế kỉ XXI là nhiều khả năng xảy ra?
Đáp án đúng là: A
Phân tích bài đọc để xác định tính chính xác của mỗi mệnh đề
Đáp án cần chọn là: A
Hạt giống của cây sồi được phát tán chủ yếu nhờ động vật, những giả thuyết nào sau đây giải thích về tốc độ dịch chuyển chậm của loài dẻ lên phía Bắc là hợp lý?
Đáp án đúng là: B; C
Phân tích bài đọc để xác định tính chính xác của mỗi mệnh đề
Đáp án cần chọn là: B; C
Đọc đoạn thông tin sau và trả lời câu 7 đến câu 14:
THỬ NGHIỆM HOẠT TÍNH THUỐC KHÁNG SINH
Một nhà khoa học đã thử nghiệm khả năng tiêt diệt một chủng vi khuẩn kháng penicillin của 5 loại thuốc mới được chế tạo
Thí nghiệm 1: Số lượng vi khuẩn kháng penicilin bằng nhau được cho vào các bình chứa 10,0 mL môi trường dinh dưỡng. Các bình được ủ trong 1 giờ ở 37°C với các nồng độ khác nhau của 5 loại thuốc. Lô đối chứng nuôi vi khuẩn trong môi trường không có bất kì loại thuốc nào. Sau khi ủ 1 giờ, vi khuẩn được rửa để loại bỏ vết thuốc sòn sót lại và được cấy lên đĩa thạch dinh dưỡng trong 7 ngày. Trong thời gian này, vi khuẩn sinh sản tạo thành các khuẩn lạc, sau đó được đếm vào cuối này thứ bảy. Lô đối chứng sau 7 ngày đếm được 50 khuẩn lạc trên đĩa nuôi cấy. Cách bố trí và kết quả của thí nghiệm 1 được thể hiện ở bảng 1
Bảng 1. Hoạt tính của thuốc tính theo nồng độ
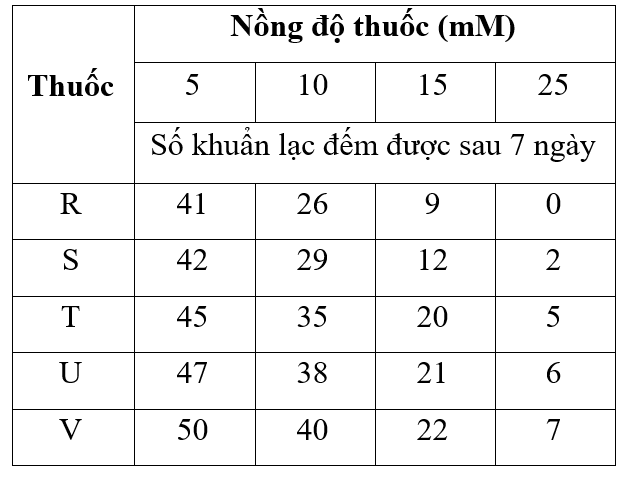
Thí nghiệm 2: Vi khuẩn được xử lí giống với thí nghiệm 1 nhưng tất cả các loại thuốc được thử nghiệm ở cùng nồng độ và áp dụng nhiều khoảng thời gian ủ với từng loại thuốc.
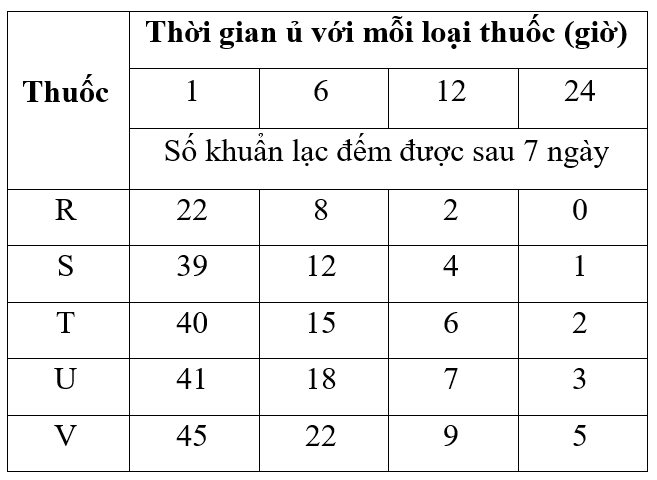
Bảng 2 cho thấy số lượng khuẩn lạc đếm được cho thí nghiệm 2
Bảng 2. Hoạt tính thuốc theo thời gian
Trả lời cho các câu 95, 96, 97, 98, 99, 100, 101 dưới đây:
Kéo thả các đáp án thích hợp vào chỗ trống
Từ kết quả của các thí nghiệm, có thể kết luận rằng: hiệu quả của các loại thuốc mới trong việc tiêu diệt vi khuẩn kháng penicillin phụ thuộc vào và thời gian ủ. Thí nghiệm 1 chỉ ra rằng: ở nồng độ , thuốc có khả năng tiêu diệt vi khuẩn hoàn toàn. Thí nghiệm 2 cho thấy rằng hiệu quả tiêu diệt vi khuẩn của tất cả các loại thuốc tăng lên theo
Đáp án đúng là: nồng độ thuốc; 25mM; R; thời gian ủ
Đọc thông tin bài đọc để tìm từ khóa thích hợp
Đáp án cần chọn là: nồng độ thuốc; 25mM; R; thời gian ủ
Nhận định dưới đây là đúng hay sai?
| Đúng | Sai | |
|---|---|---|
| a) Khi sử dụng nồng độ thuốc càng cao thì khả năng tiêu diệt vi khuẩn càng mạnh. | ||
| b) Với cả 5 loại thuốc, thời gian ủ đạt hiệu quả diệt khuẩn tốt nhất là 24h. | ||
| c) Số khuẩn lạc đếm được trên mỗi đĩa thạch nuôi cấy càng nhiều thì khả năng kháng thuốc của vi khuẩn đối với thuốc đó càng lớn |
Đáp án đúng là: Đ; Đ; Đ
Phân tích số liệu trong bảng 1
Đáp án cần chọn là: Đ; Đ; Đ
Quy trình thí nghiệm được sử dụng trong thí nghiệm 2 khác với thí nghiệm 1 là:
Đáp án đúng là: B
So sánh hai điều kiện thí nghiệm
Đáp án cần chọn là: B
Thí nghiệm 1 được thực hiện trên tổng số bao nhiêu đĩa thạch nuôi cấy vi sinh vật?
Đáp án đúng là: D
Dựa vào cách bố trí thí nghiệm 1
Đáp án cần chọn là: D
Phát biểu nào sau đây mô tả đúng nhất mối quan hệ giữa thời gian ủ và số lượng vi khuẩn sống trong Thí nghiệm 2?
Đáp án đúng là: B
Phân tích số liệu trong bảng 2
Đáp án cần chọn là: B
Để đạt hiệu quả diệt khuẩn trên 50%, phải sử dụng các loại thuốc như thế nào?
Đáp án đúng là: C
So sánh với số lượng vi khuẩn ở lô đối chứng
Đáp án cần chọn là: C
Hãy cho biết những nhận định nào sau đây về hiệu quả tiêt diệt vi khuẩn của các loại thuốc kháng sinh là đúng?
Đáp án đúng là: B; D
Phân tích số liệu bảng 1 và bảng 2
Đáp án cần chọn là: B; D