Câu nào trong các câu sau không phải là mệnh đề?
Đáp án đúng là: C
Định nghĩa mệnh đề.
Đáp án cần chọn là: C
Cho tập hợp $A = \left\{ 0;2 \right\}$. Khẳng định nào sau đây SAI ?
Đáp án đúng là: B
Phân biệt kí hiệu tập con và kí hiệu phần tử thuộc tập hợp.
Đáp án cần chọn là: B
Cho vectơ $\overset{\rightarrow}{a}$ khác $\overset{\rightarrow}{0}$ và số thực k khác 0 . Khẳng định nào sau đây đúng ?
Đáp án đúng là: B
Xét từng đáp án.
Sử dụng lý thuyết về hướng của hai vectơ, tích của một vectơ với một số.
Đáp án cần chọn là: B
Cho $\overset{\rightarrow}{a}$ và $\overset{\rightarrow}{b}$ là hai vectơ ngược hướng và đều khác vectơ $\overset{\rightarrow}{0}$. Khẳng định nào sau đây đúng?
Đáp án đúng là: C
Sử dụng định nghĩa và tính chất của hai vectơ ngược hướng.
Đáp án cần chọn là: C
Cho tam giác $\bigtriangleup ABC$ là tam giác vuông cân tại $A$. Khi đó $(\overset{\rightarrow}{AB};\overset{\rightarrow}{AC})$ có số đo bằng
Đáp án đúng là: B
Xác định góc giữa hai vectơ.
Đáp án cần chọn là: B
Xét hệ bất phương trình bậc nhất hai ẩn $\left\{ \begin{array}{l} {2x + y \leq 2} \\ {2x + y \geq - 1} \end{array} \right.$ (1). Mệnh đề nào dưới đây sai?
Đáp án đúng là: C
Xác định miềm nghiệm của hệ bất phương trình.
Đáp án cần chọn là: C
Phủ định của mệnh đề: " $\forall x \in {\mathbb{R}}:x^{2} + 1 > 0$ " là:
Đáp án đúng là: B
Để phủ định một mệnh đề có lượng từ "$\forall$" (với mọi), ta đổi thành "$\exists$" (tồn tại).
Để phủ định một mệnh đề có dấu bất đẳng thức, ta đổi dấu bất đẳng thức theo quy tắc:
- Phủ định của ">" là "$\leq$".
- Phủ định của "<" là "$\geq$".
- Phủ định của "$\geq$" là "<".
- Phủ định của "$\leq$" là ">".
- Phủ định của "=" là "$\neq$".
Đáp án cần chọn là: B
Cho ba điểm I, A, B được biểu diễn như hình vẽ sau

Khẳng định nào sau đây đúng?
Đáp án đúng là: C
Quan sát hình vẽ, có $\overset{\rightarrow}{IB}$ và $\overset{\rightarrow}{IA}$ là 2 vectơ cùng hướng và $IB = \dfrac{3}{5}IA$
Đáp án cần chọn là: C
Điểm nào dưới đây thuộc miền nghiệm của bất phương trình $2x - 3y \geq 7$ ?
Đáp án đúng là: D
Để kiểm tra xem một điểm có thuộc miền nghiệm của bất phương trình hay không, ta thay tọa độ $(x;y)$ của điểm đó vào bất phương trình. Nếu bất đẳng thức thu được là đúng, thì điểm đó thuộc miền nghiệm.
Đáp án cần chọn là: D
Cho tập hợp $X = \left\{ x \in {\mathbb{R}} \mid x - 1 > 0 \right\}$. Hãy chọn khẳng định đúng.
Đáp án đúng là: B
Để xác định tập hợp X, ta cần giải bất phương trình điều kiện cho các phần tử của tập hợp.
Đáp án cần chọn là: B
Cho ba điểm phân biệt A, B, C. Khi đó: $\overset{\rightarrow}{CA} + \overset{\rightarrow}{AB} =$
Đáp án đúng là: C
Phép cộng vectơ.
Đáp án cần chọn là: C
Cặp số $(x;y) = (3;1)$ là nghiệm của những bất phương trình bậc nhất hai ẩn nào trong các bất phương trình sau: (I): $x - y > 2$, (II): $x - y < 2$, (III): $x - y \geq 2$ và (IV): $x - y \leq 2$?
Đáp án đúng là: A
Nhận biết nghiệm của bất phương trình bậc nhất hai ẩn.
Đáp án cần chọn là: A
Cho bất phương trình \(-2 x+3 y>3\). Khi đó:
| Đúng | Sai | |
|---|---|---|
| a) \((0 ; 0)\) không là nghiệm bất phương trình. | ||
| b) \((-1 ; 1)\) không là nghiệm bất phương trình. | ||
| c) \((0 ; 1)\) không là nghiệm bất phương trình. | ||
| d) \((1 ; 3)\) là nghiệm bất phương trình. |
Đáp án đúng là: Đ; S; Đ; Đ
Để kiểm tra một cặp số \((x; y)\) có phải là nghiệm của bất phương trình hay không, ta chỉ cần thay các giá trị \(x\) và \(y\) vào bất phương trình và kiểm tra xem nó có thỏa mãn hay không.
Đáp án cần chọn là: Đ; S; Đ; Đ
Cho tập hợp $A = \left\{ 0;2;3;7 \right\}$ và tập hợp $B = \left\{ - 1;3 \right\}$
| Đúng | Sai | |
|---|---|---|
| a) $A \cap B = \varnothing$. | ||
| b) Tập hợp $B$ có 4 phần tử. | ||
| c) $7 \in A$. | ||
| d) $A \cup B = \left\{ 2;3;5; - 1;7 \right\}$. |
Đáp án đúng là: S; S; Đ; S
- Giao của hai tập hợp ($A \cap B$) là tập hợp các phần tử chung của cả $A$ và $B$.
- Hợp của hai tập hợp ($A \cup B$) là tập hợp tất cả các phần tử thuộc $A$ hoặc thuộc $B$ (mỗi phần tử chỉ liệt kê một lần).
- Kí hiệu $x \in A$ nghĩa là phần tử $x$ thuộc tập hợp $A$.
- Số phần tử của một tập hợp là số lượng các phần tử riêng biệt trong tập hợp đó.
Đáp án cần chọn là: S; S; Đ; S
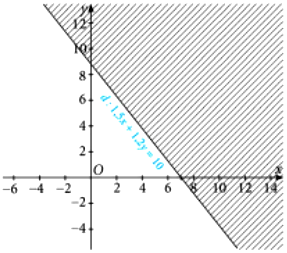
Một cửa hàng dành tối đa 10 triệu để nhập \(x\) tạ gạo và \(y\) tạ mì. Biết mỗi tạ gạo mua hết 1,5 triệu, mỗi tạ mì mua hết 1,2 triệu. Khi đó:
| Đúng | Sai | |
|---|---|---|
| a) Bất phương trình biểu thị mối liên hệ giữa \(x\) và \(y\) là: \(1,5 x+1,2 y \leq 10\). | ||
| b) Bất phương trình biểu thị mối liên hệ giữa \(x\) và \(y\) là: \(1,5 x+1,2 y \geq 10\). | ||
| c) Miền nghiệm của bất phương trình \(1,5 x+1,2 y \leq 10\) là nửa mặt phẳng bờ là đường thẳng \(d: 1,5 x+1,2 y=10\) chứa điểm \(O(0 ; 0)\) | ||
| d) Miền nghiệm của bất phương trình \(1,5 x+1,2 y \leq 10\) là nửa mặt phẳng bờ là đường thẳng \(d: 1,5 x+1,2 y=10\) không chứa điểm \(O(0 ; 0)\) |
Đáp án đúng là: Đ; S; Đ; S
Lập bất phương trình bậc nhất hai ẩn.
Biểu diễn miền nghiệm của bất phương trình đó.
Đáp án cần chọn là: Đ; S; Đ; S
Một cuộc khảo sát về khách du lịch thăm tỉnh Quảng Bình cho thấy trong 800 khách du lịch được phỏng vấn có 550 khách du lịch đến thăm động Phong Nha, 420 khách du lịch đến thăm động Thiên Đường. Có 60 khách du lịch không đến thăm cả hai địa điểm trên.
| Đúng | Sai | |
|---|---|---|
| a) Có 420 khách du lịch, trong số người được phỏng vấn, đến thăm động Thiên Đường. | ||
| b) Có 740 khách du lịch, trong số người được phỏng vấn, đến ît nhất một trong hai địa điểm trên. | ||
| c) Có 250 khách du lịch, trong số người được phỏng vấn, vừa đến thăm động Phong Nha vừa đến thăm động Thiên Đường ở tỉnh Quảng Bình? | ||
| d) Có 510 khách du lịch, trong số người được phỏng vấn, chỉ đến thăm đúng một địa điểm trong hai địa điểm nói trên. |
Đáp án đúng là: Đ; Đ; S; Đ
Đáp án cần chọn là: Đ; Đ; S; Đ
Lớp 10A9 có 45 học sinh, trong đó mỗi học sinh giōi ít nhất một trong hai môn Toán và Văn, biết rằng có 25 bạn học giỏi môn Toán, 35 bạn học giōi môn Văn. Hỏi lớp 10A9 có bao nhiêu bạn học sinh giỏi cả hai môn Toán và Văn?
Đáp án đúng là:
Công thức $n(T \cup V) = n(T) + n(V) - n(T \cap V)$.
Đáp án cần điền là: 15
Bác Nam có 7 sào đất dự định trồng hai loại hoa màu là đậu và cà chua. Biết rằng một sào trồng đậu cần 20 công và lãi được 2,5 triệu đồng, một sào trồng cà chua cần 30 công và lãi được 3,5 triệu đồng. Để thu được tiền lãi cao nhất bác Nam cần trồng $x$ (sào) đậu và $y$ (sào) cà chua. Biết bác Nam chỉ có thể sử dụng không quá 180 công cho việc trồng đậu và cà chua. Tính $3x - y$.
Đáp án đúng là:
Lập hệ bất phương trình bậc nhất hai ẩn $x,y.$
Giải hệ bất phương trình.
Đáp án cần điền là: 5
Trong mặt phẳng tọa độ Oxy , cho vecto $\overset{\rightarrow}{a} = - 2\overset{\rightarrow}{i} + 3\overset{\rightarrow}{j}$. Tính tổng hoành độ và tung độ của $\overset{\rightarrow}{a}$.
Đáp án đúng là:
Xác định toạ độ vectơ.
Đáp án cần điền là: 1
Trong mặt phẳng tọa độ Oxy, cho hai điểm $A(1; - 3);B( - 1;2)$. Điểm $M(x;y)$ thoả mãn $\overset{\rightarrow}{AB} = \overset{\rightarrow}{BM}$. Tính giá trị của $y$.
Đáp án đúng là:
Xác định toạ độ $\overset{\rightarrow}{AB}$ và $\overset{\rightarrow}{BM}$. Hai vectơ bằng nhau khi hoành độ của chúng bằng nhau, tung độ của chúng bằng nhau.
Đáp án cần điền là: 7
Tính tổng các giá trị của tham số $m$ để hệ $\left\{ \begin{array}{l} {x + \left( {m^{2} - 1} \right)y^{2} \geq 1} \\ {2y + \left( {1 - m} \right)y^{3} - 2 < 0} \end{array} \right.$ là hệ bất phương trình bậc nhất hai ẩn.
Đáp án đúng là:
Một hệ gồm có các bất phương trình bậc nhất hai ẩn được gọi là hệ bất phương trình bậc nhất hai ẩn.
Đáp án cần điền là: 1
Trong mặt phẳng $Oxy$, cho tam giác $ABC$ có $A\left( {- 2;0} \right)$; $B\left( {0;3} \right)$ và $C\left( {3; - 2} \right)$. Tính tổng tất cả các giá trị nguyên của $b$ sao cho điểm $M\left( {b;b + 2} \right)$ nằm trên hình tam giác $ABC$ tính cả ba cạnh $AB,BC,CA$.
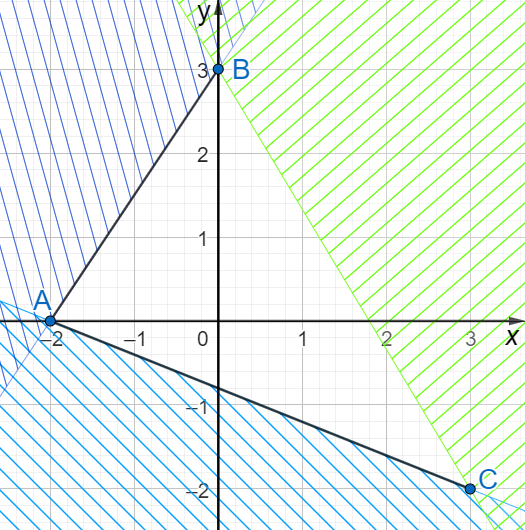
Đáp án đúng là:
Hình tam giác $ABC$ tính cả 3 cạnh của nó là miền nghiệm của hệ bất phương trình gồm 3 bất phương trình có miền nghiệm là nửa mặt phẳng chứa điểm $O\left( {0;0} \right)$ và lần lượt có các bờ là các đường $AB,BC,CA$.
Viết phương trình các đường thẳng $AB,BC,CA$ và dựa vào hình vẽ, xác định các bất phương trình tương ứng lập thành hệ bất phương trình.
Điểm $M\left( {b;b + 2} \right)$ nằm trên hình tam giác $ABC$ tính cả ba cạnh của nó khi và chỉ khi $\left( {b;b + 2} \right)$là một nghiệm của hệ, thay toạ độ điểm M vào hệ BPT, tìm b.
Đáp án cần điền là: -3