Phần 1: Toán học và xử lý số liệu
Cho hàm số \(f(x)=\log _2\left(x^2+1\right)\). Khi đó \(f^{\prime}(1)\) bằng
Đáp án đúng là: B
Tính đạo hàm của hàm số sơ cấp.
Đáp án cần chọn là: B
Cho hai biến cố \(A\) và \(B\), với \(P(A)=0,6, P(B)=0,7, P(A \cap B)=0,3\). Tính \(P(\bar{B} \mid A)\).
Đáp án đúng là: B
Đáp án cần chọn là: B
Trong một dãy số nguyên dương, biết rằng từ số thứ 3 trở đi, các số luôn bằng tích của hai số đứng ngay trước đó. Nếu số thứ 6 có giá trị là 4000 thì số đầu tiên là bao nhiêu?
Đáp án đúng là: C
Lập dãy số theo yêu cầu đầu bài.
Đáp án cần chọn là: C
Cho hàm số \(y=x^3+(1-2 m) x^2+2(2-m) x+4\). Với giá trị nào của tham số \(m\) thì đồ thị hàm số có hai điểm cực trị nằm về hai phía của trục hoành?
Đáp án đúng là: B
Đáp án cần chọn là: B
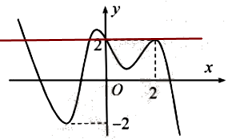
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên. Phương trình \(f\left( {f\left( x \right) - 1} \right) = 0\) có tất cả bao nhiêu nghiệm thực phân biệt?
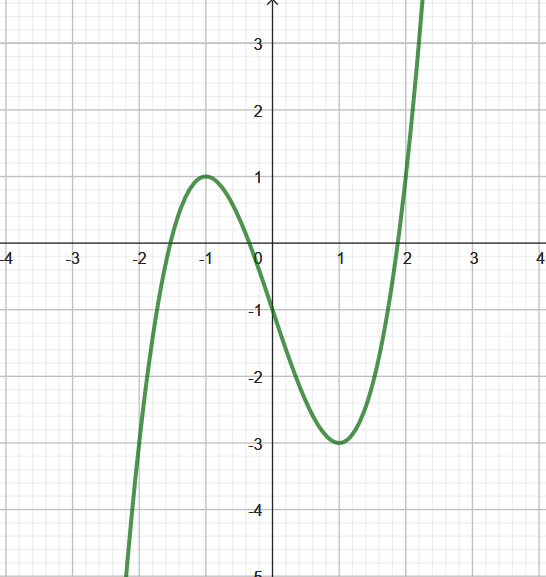
Đáp án đúng là: C
Đưa về tương giao đồ thị
Đáp án cần chọn là: C
Trong không gian Oxyz, xét mặt cầu (S) có phương trình dạng \({x^2} + {y^2} + {z^2} - 4x + 2y - 2az + 10a = 0\). Tập hợp các giá trị thực của a để (S) có chu vi đường tròn lớn bằng \(8\pi \) là:
Đáp án đúng là: C
Mặt cầu \(\left( S \right):\,\,{x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) có bán kính \(R = \sqrt {{a^2} + {b^2} + {c^2} - d} \).
Đường tròn lớn của bán kính bằng bán kính mặt cầu.
Chu vi đường tròn bán kính R là \(C = 2\pi R.\)
Đáp án cần chọn là: C
Trong mặt phẳng tọa độ \(Oxy\), đường tròn \((C)\) đi qua 3 điểm \(M(2 ;-2), N(3 ;-1), P(-1 ;-3)\) có bán kính bằng bao nhiêu (nhập đáp án vào ô trống)?
Đáp án đúng là: 5
Viết phương trình đường tròn đi qua 3 điểm.
Đáp án cần điền là: 5
Thống kê tổng số giờ nắng trong tháng 9 tại một trạm quan trắc đặt ở Cà Mau trong các năm từ 2002 đến 2021 được thống kê như sau:

Độ lệch chuẩn của mẫu số liệu ghép nhóm này là:
Đáp án đúng là: B
Áp dụng công thức tính phương sai và độ lệch chuẩn: \({s^2} = \dfrac{{{m_1}{{\left( {{x_1} - \bar x} \right)}^2} + \ldots + {m_k}{{\left( {{x_k} - \bar x} \right)}^2}}}{n}\); \(s = \sqrt {{s^2}} \)
Đáp án cần chọn là: B
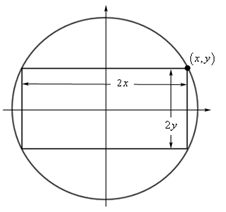
Một kiến trúc sư muốn thiết kế một khung cửa sổ hình chữ nhật lắp vào một ô tròn trên tường có bán kính 4 mét. Kiến trúc sư muốn cửa sổ có kích thước lớn nhất để đón ánh sáng vào căn phòng. Hỏi diện tích lớn nhất của cửa sổ có thể đạt được là bao nhiêu?
Đáp án đúng là: C
- Bài toán yêu cầu tìm diện tích lớn nhất của hình chữ nhật nội tiếp hình tròn có bán kính bằng 4.
- Đặt trục tọa độ với tâm đường tròn trùng với gốc tọa độ. Lập phương trình đường tròn và biểu
diễn hàm diện tích của hình chữ nhật.
- Tính đạo hàm của hàm diện tích và tìm giá trị lớn nhất của hàm số.
Đáp án cần chọn là: C
Trong không gian \(Oxyz\) cho các điểm \(A\left( {2;0;0} \right)\), \(B\left( {0;4;0} \right)\), \(C\left( {0;0;6} \right)\), \(D\left( {2;4;6} \right)\). Gọi \(\left( P \right)\)là mặt phẳng song song với mặt phẳng \(\left( {ABC} \right)\),\(\left( P \right)\) cách đều \(D\) và mặt phẳng \(\left( {ABC} \right)\). Phương trình của mặt phẳng \(\left( P \right)\) là \(ax + by + 2z + d = 0\) với \(a,b,d \in \mathbb{Z}\). Giá trị của \(d\) bằng bao nhiêu?
Đáp án đúng là: D
Đáp án cần chọn là: D
Cho một hộp kín có 6 thẻ ATM của BIDV và 4 thẻ ATM của Vietcombank. Lấy ngẫu nhiên lần lượt 2 thẻ (lấy không hoàn lại). Tìm xác suất để lần thứ hai lấy được thẻ ATM của Vietcombank nếu biết lần thứ nhất đã lấy được thẻ ATM của BIDV.
Đáp án đúng là: D
Đáp án cần chọn là: D
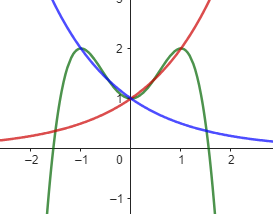
Cho hàm số \(f\left( x \right) = a{x^4} + b{x^2} + c\) với \(a \ne 0\), có đồ thị là đường cong trong hình vẽ. Phương trình \({2^x}{f^2}\left( x \right) - \left( {{4^x} + 1} \right)f\left( x \right) + {2^x} = 0\) có bao nhiêu nghiệm thực phân biệt?
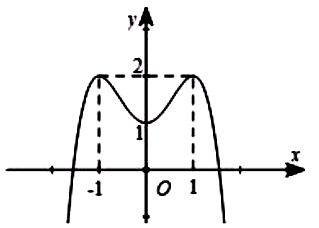
Đáp án đúng là: A
Giải phương trình bậc hai tìm \(f\left( x \right)\)
Đáp án cần chọn là: A
Cho \(f(x) = m{x^2} - 2(m - 2)x + m - 3\) . Có bao nhiêu giá trị nguyên của m để \(f\left( x \right) \le 0\forall x \in R\)
Đáp án đúng là: A
Đáp án cần chọn là: A
Số đo ba kích thước của hình hộp chữ nhật lập thành một cấp số nhân. Biết thể tích của khối hộp là 125cm3 và diện tích toàn phần là \(175c{m^2}\). Tổng số đo ba kích thước của hình hộp chữ nhật đó là bao nhiêu (nhập đáp án vào ô trống)?
Đáp án đúng là: 35/2
Gọi số đo ba kích thước của hình hộp chữ nhật là \({u_1},{u_2},{u_3}\)
Lập hệ phương trình chứa \({u_1},{u_2},{u_3}\) từ các giả thiết.
Áp dụng công thức số hạng tổng quát của cấp số nhân \({u_n} = {u_1}{q^{n - 1}}\)
Đáp án cần điền là: 35/2
Cho hàm số \(f(x)\) là hàm bậc ba. Đồ thị \(y=f^{\prime}(x)\) như hình dươi. Hàm số \(g(x)=f(x)-x\) nghịch biến trên khoảng \((a;2)\). Tính \(a\) (nhập đáp án vào ô trống).
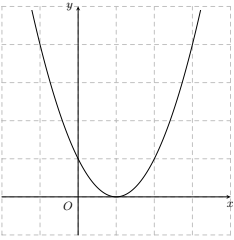
Đáp án đúng là: 0
Tính \(g'(x)\), giải phương trình \(g^{\prime}(x)=0\).
Đáp án cần điền là: 0
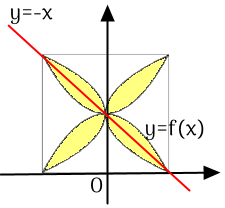
Một viên gạch hoa hình vuông cạnh 40cm. Người thiết kế đã sử dụng bốn đường parabol có chung đỉnh tại tâm viên gạch để tạo ra bốn cánh hoa .

Diện tích mỗi cánh hoa của viên gạch bằng \(S = \dfrac{a}{b}\left( {{\rm{\;c}}{{\rm{m}}^2}} \right)\) với \(a,b \in \mathbb{N};b \ne 0;{\rm{a}}\) và b nguyên tố cùng nhau. Tính \(a + b\)?
Đáp án đúng là: C
Đưa về tính diện tích bằng tích phân
Đáp án cần chọn là: C
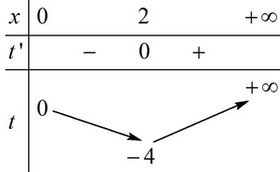
Một cái hồ chứa 600 lít nước ngọt. Người ta bơm nước biển có nồng độ muối \(30 \mathrm{~g} / \mathrm{l}\) vào hồ với tốc độ 15 (l/phút). Nồng độ muối trong hồ khi \(t\) dần về dương vô cùng (đơn vị \(\mathrm{g} / \mathrm{l}\) ) là
Đáp án đúng là: C
Đáp án cần chọn là: C
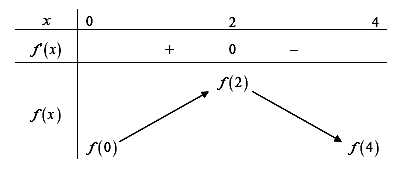
Cho hàm số \(y = f\left( x \right)\). Đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ bên dưới.
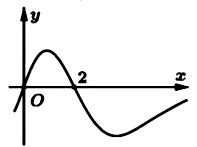
Biết rằng \(f\left( 0 \right) + f\left( 1 \right) - 2f\left( 2 \right) = f\left( 4 \right) - f\left( 3 \right)\). Giá trị nào sau đây là giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ {0;4} \right]\) ?
Đáp án đúng là: D
Lập bảng biến thiên và so sánh
Đáp án cần chọn là: D
Trên mặt phẳng tọa độ \(Oxy\), tiếp tuyến của đồ thị hàm số \(y = {x^3} + 3{x^2} - 6x + 1\) tại điểm có hoành độ bằng \(1\) và cắt hai trục tọa độ tại A, B. Tính diện tích tam giác \(OAB\) (nhập đáp án vào ô trống).
Đáp án đúng là: 8/3
Tìm phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng \(1\).
Xác định tọa độ điểm \(A,B\), độ dài \(OA,OB\).
Tính diện tích tam giác vuông \(OAB\).
Đáp án cần điền là: 8/3
Cho hàm số \(y = f(x)\) có đạo hàm trên \(\mathbb{R}\). Đồ thị hàm số \(y = {f^\prime }(x)\) như hình bên. Hỏi đồ thị hàm số \(y = f(x) - 2x\) có bao nhiêu điểm cực trị?
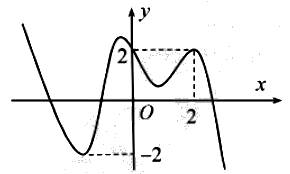
Đáp án đúng là: A
Tính y’ và tìm số nghiệm y’ = 0. Lưu ý cực trị là các điểm mà y' đi qua đổi dấu
Đáp án cần chọn là: A
Cô giáo có \(12\) phần quà gồm \(4\) phần loại \(I\) và \(8\) phần loại \(II\) được đựng trong \(12\) hộp kín giống nhau. Cô chia đều cho \(3\) bạn, mỗi bạn \(4\) phần quà. Xác suất để mỗi bạn đều nhận được cả hai loại quà là (nhập đáp án vào ô trống).
Đáp án đúng là: 32/55
Tính xác suất theo định nghĩa cổ điển.
Đáp án cần điền là: 32/55
Bạn Nam chơi trò xếp tháp bằng các que diêm theo quy tắc thể hiện như hình vẽ:
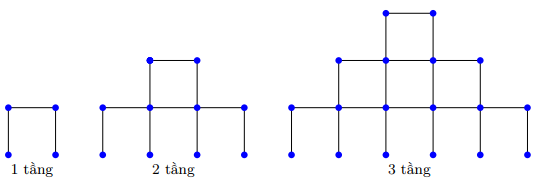
Bạn Nam có 212 que diêm thì có thể xếp được tháp cao nhất bao nhiêu tầng (nhập đáp án vào ô trống)?
Đáp án đúng là: 10
Đáp án cần điền là: 10
Một cửa hiệu nọ chuyên kinh doanh giày và dép. Dựa trên doanh số bán hàng trong một thời gian dài, xác suất để khách mua hàng tại cửa hiệu mua giày là 75%. Trong số những khách hàng mua giày, có 60% khách hàng cũng mua vớ và trong số những khách hàng mua dép, có 90% khách hàng không mua vớ. Một khách hàng đến cửa hiệu đó để mua hàng. Tính xác suất để khách hàng đó mua vớ.
Đáp án đúng là: B
Áp dụng công thức xác suất toàn phần: \(P\left( A \right) = P\left( B \right).P\left( {A\left| B \right.} \right) + P\left( {\overline B } \right).P\left( {A\left| {\overline B } \right.} \right)\).
Đáp án cần chọn là: B
Cho hàm số \(f\left( x \right)\) thoả mãn \(\int {f\left( x \right)} dx = {e^{2x}} + C\). Khẳng định nào sau đây đúng?
Đáp án đúng là: A
\(\int {f\left( x \right)} dx = {e^{2x}} + C \Rightarrow f\left( x \right) = {\left( {{e^{2x}} + C} \right)^\prime }\)
Đáp án cần chọn là: A
Một người quan sát đỉnh của một ngọn núi nhân tạo từ hai vị trí khác nhau của tòa nhà. Lần đầu tiên người đó quan sát đỉnh núi từ tầng trệt với phương nhìn tạo với phương nằm ngang \({35^0}\) và lần thứ hai người này quan sát tại sân thượng của cùng tòa nhà đó với phương nằm ngang \({15^0}\) (như hình vẽ). Tính chiều cao ngọn núi biết rằng tòa nhà cao \(60\left( m \right)\).
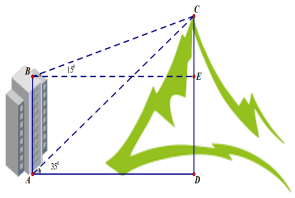
Đáp án đúng là: B
- Tính góc \(\angle CBA\).
- Tính góc \(\angle BCA.\).
- Tính AC dựa vào định lí sin trong tam giác CBA.
- Tính CD dựa vào tam giác CAD vuông tại D.
Đáp án cần chọn là: B
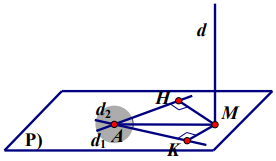
Trong không gian tọa độ Oxyz, cho điểm \(A(2 ; 1 ; 1)\), mặt phẳng \((P): x-z-1=0\) và đường thẳng \((d):\left\{\begin{array}{l}x=1-t \\ y=2 \\ z=-2+t\end{array}\right.\). Gọi \(d_1 ; d_2\) là các đường thẳng đi qua \(A\), nằm trong \((P)\) và đều có khoảng cách đến đường thẳng \(d\) bằng \(\sqrt{6}\). Côsin của góc giữa \(d_1\) và \(d_2\) bằng
Đáp án đúng là: B
Đáp án cần chọn là: B
Một ô tô bắt đầu chuyển động nhậnh dần đều với vận tốc \(v_1(t)=7 t(\mathrm{~m} / \mathrm{s})\). Đi được 5 s , người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc \(a=-70\left(\mathrm{~m} / \mathrm{s}^2\right)\). Tính quãng đường \(S\) đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn (nhập đáp án vào ô trống)
Đáp án đúng là: 385/4
Ứng dụng tích phân để tính quãng đường.
Đáp án cần điền là: 385/4
Có bao nhiêu giá trị nguyên của \(k\) để tam thức \(y=x^2-2(4 k-1) x+15 k^2-2 k-7\) luôn dương trên \(\mathbb{R}\) (nhập đáp án vào ô trống).
Đáp án đúng là: 1
Để tam thức \(y=a x^2+b x+c>0\) với \(\forall x \in \mathbb{R}\) thì \(\left\{\begin{array}{l}a>0 \\ \Delta<0\end{array}\right.\) hoặc \(\left\{\begin{array}{l}a>0 \\ \Delta^{\prime}<0 .\end{array}\right.\)
Đáp án cần điền là: 1
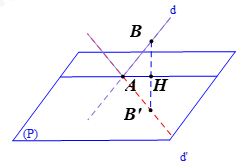
Trong không gian với hệ trục tọa độ vuông góc \(Oxyz\), cho đường thẳng \(d:\dfrac{x}{1} = \dfrac{{y + 1}}{2} = \dfrac{{z - 2}}{{ - 1}}\) và mặt phẳng \(\left( P \right):x + y + z - 3 = 0\). Phương trình đường thẳng d' đối xứng với d qua (P) là
Đáp án đúng là: B
Bước 1: Lấy điểm \(B\left( {0; - 1;2} \right)\) thuộc d.
Bước 2: Tìm giao điểm A của d và (P)
Bước 3: Gọi H là hình chiếu của B lên (P), B’ là điểm đối xứng B qua (P). Tìm d’
Đáp án cần chọn là: B
Một chiếc máy bay chuyển động trên đường băng với vận tốc \(v(t)=t^2+10 t(\mathrm{~m} / \mathrm{s})\), với \(t\) là thời gian được tính theo đơn vị giây kế từ khi máy bay bắt đầu chuyển động. Biết khi máy bay đạt vận tốc \(200(\mathrm{~m} / \mathrm{s})\) thì nó rời đường băng. Quãng đường máy bay đã di chuyển trên đường băng là:
Đáp án đúng là: A
Đáp án cần chọn là: A
Cho \(\int_{\frac{\pi}{6}}^{\frac{\pi}{4}}(2 \tan x+\cot x)^2 \mathrm{~d} x=a+b \sqrt{3}+c \pi(*)\). Biết rằng, tồn tại duy nhất bộ ba số hữu tỉ \(a, b, c\) thỏa mãn (*). Tổng \(a+3b+12c\) có giá trị bằng bao nhiêu (nhập đáp án vào ô trống)?
Đáp án đúng là: 1
Đáp án cần điền là: 1
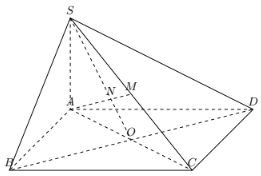
Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình bình hành. Gọi \(M\) là trung điểm \(SC\); \(N\) là giao điểm của \(AM\) và \((SBD)\). Tính tỉ số \(\dfrac{N M}{N A}\).
Đáp án đúng là: B
Đáp án cần chọn là: B
Tiệm cận xiên của đồ thị hàm số : \(y = \dfrac{{{x^3}}}{{{x^2} - 1}}\) là?
Đáp án đúng là: C
Dùng giới hạn xác định tiệm cận xiên
Đáp án cần chọn là: C
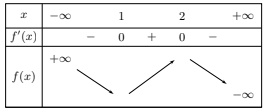
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
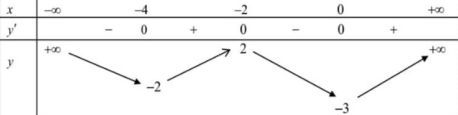
Số giá trị nguyên của tham số \(m\) để phương trình \(3f\left( {{x^2} - 4x} \right) = m + 5\) có ít nhất 5 nghiệm thực phân biệt thuộc khoảng \(\left( {0; + \infty } \right)\) là:
Đáp án đúng là: B
- Đặt \(t = {x^2} - 4x\), với \(x \in \left( {0; + \infty } \right)\), đưa phương trình về dạng \(f\left( t \right) = m\,\,\left( * \right)\).
- Xác định mỗi nghiệm \(t\) cho bao nhiêu nghiệm \(x\) trên từng khoảng cụ thể.
- Tìm điều kiện về số nghiệm của phương trình (*) để phương trình ban đầu có ít nhất 5 nghiệm phân biệt.
Đáp án cần chọn là: B
Trong không gian Oxyz, cho mặt cầu \((S): x^2+(y-1)^2+z^2=2\). Trong các điểm cho dưới đây, điểm nào nằm ngoài mặt cầu (S) ?
Đáp án đúng là: C
Đáp án cần chọn là: C
Trong hệ trục tọa độ \(Oxy\), cho \(A(1 ; 1), B(-1 ; 3)\) và \(H(0 ; 1)\). Biết \(C\) là điểm sao cho \(H\) là trực tâm \(\triangle ABC\). Tìm hoành độ điểm \(C\) (nhập đáp án vào ô trống).
Đáp án đúng là: -1
Gọi tọa độ điểm C.
\(H\) là trực tâm \(\triangle A B C\) \(\Leftrightarrow\left\{\begin{array}{l}\overrightarrow{C H} \cdot \overrightarrow{A B}=0 \\ \overrightarrow{A H} \cdot \overrightarrow{B C}=0\end{array} \right.\)
Đáp án cần điền là: -1
Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right)\) : \({x^2} + {y^2} + {z^2} - 2z - 3 = 0\) và điểm \(A\left( {2;2;2} \right)\). Biết rằng từ \(A\) có thể kẻ được các tiếp tuyến đến mặt cầu \(\left( S \right)\), đồng thời các tiếp điểm luôn thuộc mặt phẳng \(\left( \alpha \right)\) có phương trình \(ax + by + cz - 5 = 0\). Mặt phẳng \(\left( \alpha \right)\) đi qua điểm nào dưới đây?
Đáp án đúng là: D
Đáp án cần chọn là: D
Kết quả bài kiểm tra giữa kì của các bạn học sinh lớp 10A được thống kê ở các biểu đồ dưới đây. Mốt của mẫu số liệu là bao nhiêu (nhập đáp án vào ô trống).
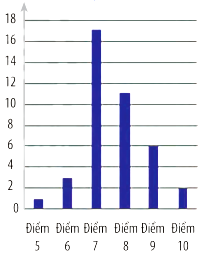
Đáp án đúng là: 7
Đáp án cần điền là: 7
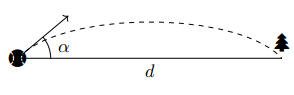
Một quả bóng golf kể từ lúc được đánh đến lúc chạm đất đã di chuyền được một khoảng cách \(d(m)\) theo phương nằm ngang. Biết rằng \(d=\dfrac{v_0^2 \sin 2 \alpha}{g}\) trong đó \(v_0(\mathrm{~m} / \mathrm{s})\) là vận tốc ban đầu của quả bóng, \(g\left(\mathrm{~m} / \mathrm{s}^2\right)\) là gia tốc trọng trường và \(\alpha\) là góc đánh quả bóng so với phương nằm ngang. Khoảng cách \(d\) là bao nhiêu centimet, biết rằng \(v_0=15(\mathrm{~m} / \mathrm{s})\); \(g=10\left(\mathrm{~m} / \mathrm{s}^2\right)\) và \(\cos \alpha=\dfrac{3}{5}\) với \(\left(0 \leq \alpha \leq 45^0\right)\) (nhập đáp án vào ô trống)?
Đáp án đúng là: 108/5
Sử dụng công thức lượng giác tính \(\sin 2 \alpha\).
Thay các giá trị đã có để tính khoảng cách \(d\).
Đáp án cần điền là: 108/5
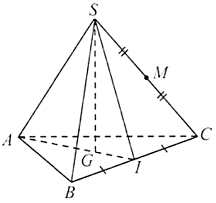
Cho hình chóp tam giác đều \(S \cdot A B C\) có cạnh đáy bằng \(3a\), cạnh bên bằng \(2a\). Gọi \(G\) là trọng tâm của tam giác \(ABC\), \(M\) là trung điểm của \(SC\). Khoảng cách từ \(M\) đến mặt phẳng \((SAG)\).
Đáp án đúng là: B
Xác định khoảng cách từ \(C\) đến mặt phẳng \((S A G)\).
Có \(d(M,(S A G))=\dfrac{1}{2} d(C,(S A G))\).
Đáp án cần chọn là: B
Thời gian truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau:

Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm này là:
Đáp án đúng là: A
Công thức tính tứ phân vị thứ nhất: \({Q_1} = {a_p} + \dfrac{{\dfrac{n}{4} - \left( {{m_1} + \ldots + {m_{p - 1}}} \right)}}{{{m_p}}} \cdot \left( {{a_{p + 1}} - {a_p}} \right)\).
Đáp án cần chọn là: A
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = {(x + 1)^{2024}}{(x - 1)^{2025}}\left( {2 - x} \right)\). Hỏi hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
Đáp án đúng là: C
Đáp án cần chọn là: C
Cho hai điểm \(P(1 ; 6)\), \(Q(-3 ;-4)\) và đường thẳng \(\Delta: 2 x-y-1=0\). Gọi \(M \in \Delta\) là điểm sao cho \(M P+M Q\) đạt giá trị nhỏ nhất. Tìm tung độ của điểm \(M\) (nhập đáp án vào ô trống).
Đáp án đúng là: -1
Gọi \(P^{\prime}\) là điểm đối xứng của \(P\) qua đường thẳng \(\Delta\).
\(M P+M Q\) đạt giá trị nhỏ nhất khi \(M, P^{\prime}, Q\) thẳng hàng.
Đáp án cần điền là: -1
Một hộp bút bi Thiên Long có 15 chiếc bút trong đó có 9 chiếc bút mới. Người ta lấy ngẫu nhiên 1 chiếc bút để sử dụng sau đó trả lại vào hộp. Lần thứ hai lấy ngẫu nhiên 2 chiếc bút, tính xác suất cả hai chiếc bút lẫy ra đều là chiếc mới.
Đáp án đúng là: A
Đáp án cần chọn là: A
Cho hàm số \(f(x)\). Biết \(f(0)=4\) và \(f^{\prime}(x)=2 \cos ^2 x+1, \forall x \in \mathbb{R}\), khi đó \(\int_0^{\frac{\pi}{4}} f(x) \mathrm{d} x\) bằng bao nhiêu? (điền đáp án vào ô trống, kết quả làm tròn đến hàng đơn vị)
Đáp án đúng là: 4
Sử dụng công thức hạ bậc lượng giác.
Tính tích phân của hàm số sơ cấp.
Đáp án cần điền là: 4
Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số \(y=\sqrt{2 x}\) và \(y=\dfrac{x^2}{2}\)
Đáp án đúng là: 4/3
Giải phương trình hoành độ giao điểm.
Ứng dụng tích phân tính diện tích hình phẳng.
Đáp án cần điền là: 4/3
Trong một đột kiểm tra sức khoẻ, có một loại bệnh \(X\) mà tỉ lệ người mắc bệnh là \(0,2 \%\) và một loại xét nghiệm \(Y\) mà ai mắc bệnh \(X\) khi xét nghiệm \(Y\) cūng có phản ứng dương tính. Tuy nhiên, có \(6 \%\) những người không bị bệnh \(X\) lại có phản ứng dương tính với xét nghiệm Y. Chọn ngẫu nhiên 1 người trong đột kiểm tra sức khoẻ đó. Giả sử người đó có phản ứng dương tính với xét nghiệm Y. Xác suất người đó bị mắc bệnh X là bao nhiêu (làm tròn kết quả đến hàng phần trăm)?
Đáp án đúng là: B
Áp dụng công thức Bayes để tính xác suất.
Đáp án cần chọn là: B
Dựa vào thông tin dưới đây và trả lời các câu hỏi từ câu 48 - 50:
Số lượng của một loại vi khuẩn X trong một phòng thí nghiệm được biểu diễn theo công thức \(S(t) = A.{e^{rt}}\), trong đó A là số lượng vi khuẩn tại thời điểm chọn mốc thời gian, r là tỉ lệ tăng trưởng (r > 0), t là thời gian tăng trưởng (tính theo đơn vị là giờ). Lúc 6 giờ sáng, số lượng vi khuẩn X là 150 con. Sau 3 giờ, số lượng vi khuẩn X là 450 con.
Trả lời cho các câu 48, 49, 50 dưới đây:
Tỉ lệ tăng trưởng của vi khuẩn X gần nhất với kết quả nào sau đây?
Đáp án đúng là: C
Giải phương trình mũ cơ bản.
Đáp án cần chọn là: C
Thời điểm số lượng vi khuẩn X gấp 9 lần số lượng vi khuẩn ban đầu là:
Đáp án đúng là: B
Giải phương trình mũ cơ bản.
Đáp án cần chọn là: B
Cùng thời điểm lúc 6 giờ, người ta đo được số lượng vi khuẩn Y là 300 con. Biết rằng số lượng vi khuẩn Y tăng 5% mỗi giờ. Hỏi vào lúc mấy giờ, số lượng vi khuẩn X bằng số lượng vi khuẩn Y.
Đáp án đúng là: B
Viết công thức tính số lượng vi khuẩn Y.
Giải phương trình mũ.
Đáp án cần chọn là: B
Phần 2: Văn học - Ngôn Ngữ
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án đúng là: A
Vận dụng kiến thức đã học về nghĩa của từ
Đáp án cần chọn là: A
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án đúng là: B
Vận dụng kiến thức đã học về nghĩa của từ
Đáp án cần chọn là: B
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án đúng là: C
Vận dụng kiến thức đã học về nghĩa của từ
Đáp án cần chọn là: C
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án đúng là: A
Vận dụng kiến thức đã học về nghĩa của từ
Đáp án cần chọn là: A
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án đúng là: B
Vận dụng kiến thức đã học về nghĩa của từ
Đáp án cần chọn là: B
Chọn cặp từ/cụm từ thích hợp nhất điền vào chỗ trống:
Càng nhiều tri thức thì ________ có thêm trí tưởng tượng, và ________ càng giàu tưởng tượng thơ mộng thì sẽ nảy sinh nhiều ý tưởng bất ngờ cho sáng tạo khoa học.
Đáp án đúng là: B
Suy luận
Đáp án cần chọn là: B
Chọn cặp từ/cụm từ thích hợp nhất điền vào chỗ trống:
________, chúng ta không thể ________ là nền văn hóa của của ta đồ sộ, có những cống hiến lớn lao cho nhân loại, hay có những đặc sắc nổi bật.
Đáp án đúng là: C
Suy luận
Đáp án cần chọn là: C
Chọn cặp từ/cụm từ thích hợp nhất điền vào chỗ trống:
Đường đi của thơ là con đường đưa thẳng vào ________, không quanh co, qua những chặng ________, những cột cây số
Đáp án đúng là: D
Suy luận
Đáp án cần chọn là: D
Chọn cặp từ/cụm từ thích hợp nhất điền vào chỗ trống:
Hiện đại hóa văn học là ________ làm cho văn hóa được phương Tây ________ thoát khỏi hệ thống thi pháp văn học trung đại để hội nhập với văn học hiện đại thế giới.
Đáp án đúng là: A
Suy luận
Đáp án cần chọn là: A
Chọn cặp từ/cụm từ thích hợp nhất điền vào chỗ trống:
Nếp nhà là sự gắn bó giữa các thành viên, là những người trong gia đình phải biết yêu thương nhau, ________ nhau, nhưng đùm bọc không có nghĩa là chấp nhận những việc làm sai trái của những người trong ________ mình.
Đáp án đúng là: A
Suy luận
Đáp án cần chọn là: A
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
Với sự nghiệp đồ sộ của mình, Tô Hoài giống hệt cây đại thụ trong khu rừng văn xuôi Việt Nam hiện đại.
Đáp án đúng là: B
Suy luận
Đáp án cần chọn là: B
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
Vào lúc sáng sớm ngày 26 tháng 03 năm 2000, cuộc thi chạy bộ đã diễn ra đầy hứng khởi với sự tham gia của hơn 100 thí sinh.
Đáp án đúng là: A
Suy luận
Đáp án cần chọn là: A
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
Đầu thế kỉ XX, nhu cầu văn hóa của lớp công chúng mới đã làm nảy sinh những hoạt động buôn bán văn hóa, dẫn đến sự phát triển của nghề in, xuất bản, làm báo.
Đáp án đúng là: C
Suy luận
Đáp án cần chọn là: C
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
Nhà văn Nguyễn Huy Tưởng có thiên tư khai khác đề tài lịch sử và có đóng góp nổi bật ở hai thể loại là kịch và tiểu thuyết.
Đáp án đúng là: A
Suy luận
Đáp án cần chọn là: A
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
Cuộc họp xuất phát từ sớm nhưng có lẽ sẽ phải kéo dài vì có rất nhiều vấn đề nổi cộm cần phải bàn bạc kĩ lưỡng.
Đáp án đúng là: A
Suy luận
Đáp án cần chọn là: A
Đọc đoạn trích dưới đây và trả lời các câu hỏi từ 66 đến 70:
Người có phẩm cách sẽ làm các việc thiện khi coi nó là chuyện đương nhiên và không tỏ ra tự mãn về nó. Cho dù là làm việc tốt nhưng nếu tự mãn thì sẽ mất đi phẩm cách và bị người khác cho rằng mình làm như vậy là vì thích được tự mãn hay háo danh. Việc tiến hành các việc thiện nổi bật, nhiều người biết tới là điều khó tránh khỏi trong giới làm kinh doanh nhằm nâng cao hình ảnh doanh nghiệp thông qua các hoạt động truyền thông, nhưng ở phạm vi riêng tư thì việc tiến hành nó trong im lặng sẽ khiến mọi người cảm động hơn. Kín đáo ở đây không có nghĩa là che giấu mà là không tỏ ra tự mãn, không làm ồn ào và khoa trương về nó. “Đức” ban đầu chỉ là chuyện làm việc thiện mà không cần chờ trả ơn.
Không chỉ hoạt động tình nguyện mà việc tiến hành trong im lặng những việc tốt, không tự mãn, khoa trương sẽ làm người ta khiêm tốn và nâng cao được phẩm cách. Trong cuốn sách có tên “Tu chứng nghĩa” nơi tập hợp những gì thuộc về bản chất của Phật giáo có đoạn viết: “Nếu hướng mặt vào nhau mà nói những lời nhân ái thì tự nhiên khuôn mặt sẽ tràn đầy hạnh phúc và trái tim trở nên an lạc. Nếu như nghe từ ai đó những lời nhân ái thì những lời nói ấy sẽ lưu lại trong tim và lay động tâm hồn”. Điều này có nghĩa là việc nghe gián tiếp từ người khác những lời tràn ngập tình yêu thương dành cho người khác sẽ khiến con người ta cảm động hơn là nghe trực tiếp khi mặt đối mặt.
(Trích Phẩm cách phụ nữ, Bando Mariko, Nguyễn Quốc Vương dịch)
Trả lời cho các câu 66, 67, 68, 69, 70 dưới đây:
Theo nội dung đoạn trích, từ nào KHÔNG cùng nhóm với các từ còn lại?
Đáp án đúng là: C
Căn cứ văn bản
Đáp án cần chọn là: C
Theo tác giả, điều gì khiến người ta cảm động hơn cả?
Đáp án đúng là: D
Căn cứ văn bản
Đáp án cần chọn là: D
Ý nào dưới đây KHÔNG phù hợp với nội dung đoạn trích?
Đáp án đúng là: B
Căn cứ nội dung bài đọc.
Đáp án cần chọn là: B
Nội dung chính của đoạn trích là gì?
Đáp án đúng là: B
Căn cứ nội dung bài đọc.
Đáp án cần chọn là: B
Theo đoạn trích, điều KHÔNG nên khi làm việc thiện là gì?
Đáp án đúng là: A
Căn cứ nội dung bài đọc
Đáp án cần chọn là: A
Đọc đoạn trích dưới đây và trả lời các câu hỏi từ 71 đến 75:
Hệ thống khí hậu gồm năm thành phần chính là khí quyển, thủy quyển, băng quyển, thạch quyển và sinh quyển. Mặc dù các thành phần này rất khác nhau về cấu trúc, thành phần, các thuộc tính vật lí và các thuộc tính khác nhưng chúng được liên kết với nhau thông qua sự trao đổi các dòng khối lượng, dòng năng lượng và động lượng để tạo nên một thể thống nhất rộng lớn. Hệ thống khí hậu tiến hóa theo thời gian dưới tác động của các nhân tố bên trong và bên ngoài. Các nhân tố bên trong chi phối hệ thống khí hậu gồm các thuộc tính của khí quyển như thành phần cấu tạo, tính chất ổn định, hoàn lưu khí quyển và các đặc tính địa phương như khoảng cách xa biển hay lục địa, độ cao địa hình, đặc điểm bề mặt đất, lớp phủ thực vật cũng như trạng thái gần các hồ, ao… Các nhân tố bên ngoài tác động đến hệ thống khí hậu gồm bức xạ mặt trời, tính chất hình cầu của Trái đất, chuyển động của Trái đất xung quanh mặt trời và sự quay quanh trục của nó, sự tồn tại của lục địa và đại dương, cũng như những tác động do con người làm thay đổi các thành phần trên Trái đất.
(Trích Ứng phó với biến đổi khí hậu ở Việt Nam, Nhiều tác giả)
Trả lời cho các câu 71, 72, 73, 74, 75 dưới đây:
Yếu tố nào KHÔNG thuộc nhân tố bên ngoài tác động đến hệ thống khí hậu?
Đáp án đúng là: C
Căn cứ nội dung bài đọc
Đáp án cần chọn là: C
Từ “chúng” (in đậm) trong đoạn trích chỉ đối tượng nào?
Đáp án đúng là: D
Căn cứ nội dung bài đọc.
Đáp án cần chọn là: D
Thông tin nào sau đây KHÔNG THỂ suy ra từ nội dung của đoạn trích?
Đáp án đúng là: B
Căn cứ nội dung bài đọc.
Đáp án cần chọn là: B
Nội dung chính của đoạn trích là gì?
Đáp án đúng là: A
Căn cứ nội dung bài đọc.
Đáp án cần chọn là: A
Theo đoạn trích, thông tin nào KHÔNG đúng về các nhân tố bên trong chi phối hệ thống khí hậu?
Đáp án đúng là: A
Căn cứ nội dung bài đọc
Đáp án cần chọn là: A
Tnú không cứu được vợ được con. Tối đó Mai chết. Còn đứa con thì đã chết rồi. Thằng lính to béo đánh một cây sắt vào ngang bụng nó, lúc mẹ nó ngã xuống, không kịp che cho nó. Nhớ không Tnú, mày cũng không cứu sống được vợ mày. Còn mày thì chúng nó bắt mày, trong tay mày chỉ có hai bàn tay trắng, chúng nó trói mày lại. Còn tau thì lúc đó đứng đằng sau gốc cây vả. Tau thấy chúng nó trói mày bằng dây rừng. Tau không nhảy ra cứu mày. Tau cũng chỉ có hai bàn tay không. Tau không ra, tau quay đi vào rừng, đi tìm giáo mác. Nghe rõ chưa, các con rõ chưa. Nhớ lấy, ghi lấy. Sau này tau chết rồi, bay còn sống phải nói cho con cháu. Chúng nó đã cầm súng mình phải cầm giáo!…
(Trích Rừng Xà Nu – Nguyễn Trung Thành)
Câu nói “Chúng nó đã cầm súng mình phải cầm giáo” thể hiện tư tưởng gì?
Đáp án đúng là: B
Đọc đoạn trích
Đáp án cần chọn là: B
Nội dung chính mà tác giả muốn làm nổi bật trong đoạn văn sau là gì?
Thực tế đã thay thế cho mộng tưởng; chẳng có bàn ăn thịnh soạn nào cả, mà chỉ có phố xá vắng teo, lạnh buốt, tuyết phủ trắng xóa, gió bấc vi vu và mấy người khách qua đường quần áo ấm áp vội vã đi đến những nơi hẹn hò, hoàn toàn lãnh đạm với cảnh nghèo khổ của em bé bán diêm.
(Trích Cô bé bán diêm)
Đáp án đúng là: C
Đọc đoạn trích
Đáp án cần chọn là: C
Đọc đoạn văn sau và trả lời câu hỏi dưới đây:
Em ơi! Hà Nội - phố!
Ta còn em mùi hoàng lan.
Ta còn em mùi hoa sữa.
Tiếng giày ai gõ nhịp đường khuya?
Cọt kẹt bước chân quen.
Thang gác thời gian
Mòn thân gỗ.
Ngôi sao lẻ lạc vào căn xép nhỏ...
Ý nào nêu đúng tác dụng của biện pháp tu từ điệp cấu trúc trong đoạn văn bản trên?
Đáp án đúng là: A
Đọc đoạn trích
Đáp án cần chọn là: A
Đọc đoạn thơ sau đây và trả lời câu hỏi:
Sen tàn, cúc lại nở hoa
Sầu dài, ngày ngắn, đông đà sang xuân
Tìm đâu cho thấy cố nhân?
Lấy câu vận mệnh khuây dần nhớ thương
Chạnh niềm nhớ cảnh gia hương
Nhớ quê, chàng lại tìm đường thăm quê
Hình ảnh hoán dụ “sen” và “cúc” trong bài thơ được hiểu là:
Đáp án đúng là: A
Đọc đoạn trích
Đáp án cần chọn là: A
Đọc đoạn trích và trả lời câu hỏi dưới đây:
Em chợt có cảm hứng muốn dắt xe đi bộ để ngắm cảnh đường làng. Bây giờ nắng đã nhuộm vàng hàng cau hai bên đường, hương cau thoang thoảng càng quyến rũ lòng người. Em lại dõi mắt nhìn theo đôi chim vừa về tổ. Chúng kêu ríu rít. Các con chim non đang chíp chíp như gọi mẹ. Hai vợ chồng chim đang mớm mồi cho chúng. Nhìn cảnh ấy, em chợt mỉm cười một mình. Chỉ một chút nữa thôi mình cũng sẽ được như những con chim non kia. Ông bà sẽ ra đón mình và sẽ dành cho minh thật nhiều món ăn ngon. Mải mê suy nghĩ em bị hụt chân bởi cái ổ gà to tướng bên đường may mà gượng kịp, không thì cả người và xe sẽ phải nằm dài trên đường rồi.
Hình ảnh chính trong đoạn trích là gì?
Đáp án đúng là: B
Đọc đoạn trích
Đáp án cần chọn là: B
Đọc đoạn trích và trả lời câu hỏi dưới đây:
Ra đến rừng săng lẻ, tôi chưa về chỗ giấu xe vội mà men ra bờ sông ngoài cầu. Con sông miền Tây in đầy bóng núi xanh thẫm, hai bên bờ cỏ lau chen với hố bom. Chiếc cầu bị cắt làm đôi như một nhát rìu phang rất ngọt. Ba nhịp phía bên này đổ sập xuống, những phiến đá xanh lớn rơi ngổn ngang dưới lòng sông, chỉ còn hai hàng trụ đứng trơ vơ giữa trời.
Đối tượng nào được miêu tả chính trong đoạn trích?
Đáp án đúng là: B
Đọc đoạn trích
Đáp án cần chọn là: B
Đọc đoạn trích và trả lời câu hỏi dưới đây:
Rồi chúng ta sẽ là người chiến thắng
Vaccine phòng ngừa, quyết sách 5K
Nồng ấm tình người tình đồng đội thiết tha
Chúng ta được về nhà với nụ cười chiến thắng!
Sao yêu quá những chiến binh thầm lặng
Từng phút từng giờ giữa sống chết bủa vây
Mang lại màu xanh hạnh phúc sum vầy
Cho Tổ quốc bình yên một ngày không xa nữa
(Trích “Trong tâm dịch Covid”, GS.TS.BS Nguyễn Đức Công, Chủ tịch Hội đồng Bảo vệ sức khỏe cán bộ miền Nam, cand.com.vn)
Dòng nào dưới đây nêu đúng nhất nội dung đoạn trích trên:
Đáp án đúng là: A
Đọc đoạn trích
Đáp án cần chọn là: A
Đọc đoạn trích và trả lời câu hỏi dưới đây:
Dòng sông trở nên đủ mạnh mẽ và xuyên qua núi hay thậm chí tạo thành một hẻm núi.{...} Khi nước gặp con người, nó còn được chứng kiến nhiều chuyện nhiều hơn. Một ông lão băng qua cây cầu, một cô gái trẻ trên chiếc xe đạp, một đôi tình nhân ngồi ngắm sông trôi. Cứ mãi chầm chậm và cứ mãi xanh, dòng sông chứng kiến lũ trẻ chơi đùa trong công viên hai bên bờ và người cha cùng cậu con nhỏ đang chơi bắt bóng. Dòng sông, giờ đã ở tuổi xế chiều, lại càng trở nên dịu dàng khi nó tiến dần ra phía biển. Rồi cũng đến lúc nó ra tới biển và dòng chảy của nước cuối cùng cũng đi tới hồi kết. Tất cả những trầm tích được nước mang theo lúc đó lắng lại ở cửa sông. Kết quả là một vùng châu thổ được hình thành. Sông Hằng, sông Missisippi và sông Amazon đều đã hình thành những châu thổ tựa như hình chiếc lược tại nơi chúng gặp gỡ biển cả. Đều có khởi nguồn như một bờ cát nhỏ cuối cùng đã phát triển thành một vùng đất rộng lớn, tạo nên một đường bờ biển mới và rộng rãi. Những vùng châu thổ màu mỡ này hình thành nên những vùng nông nghiệp vĩ đại nhất trên thế giới- món quà cuối cùng mà nước dành tặng cho loài người, trước khi nó hiển mình cho đại dương vào lúc cuối đời.
(Trích Bí mật của nước, Masaru Emoto, NXB Lao động, 2019, tr.90-93)
“Nó” trong câu văn sau là để chỉ đối tượng nào? “Khi nước gặp con người, nó còn được chứng kiến nhiều chuyện nhiều hơn”
Đáp án đúng là: C
Đọc đoạn trích
Đáp án cần chọn là: C
Đọc đoạn trích và trả lời câu hỏi dưới đây:
“Bản chất của áp lực là dương, nên cuộc sống luôn phải có một số áp lực Một đứa trẻ không vượt qua nổi áp lực, sau này lớn lên, tôi tin đứa trẻ đó sẽ rất khó thành công trong cuộc sống. Nhưng có áp lực chịu được, có áp lực độc hại. Với một đứa trẻ, để dạy chúng “tự lái”, cha mẹ nên biết tạo áp lực vừa phải, đủ giúp chúng kiểm soát tốt bản thân và để cha mẹ hiểu tâm sinh lý, khả năng của con nhằm đồng hành với chúng.
(Áp lực thành tích - Trần Văn Phúc, Vnexpress, Thử bay. 18/12/2021)
Anh/ chị hiểu như thế nào về áp lực độc hại được tác giả nhắc đến trong đoạn trích?
Đáp án đúng là: B
Đọc đoạn trích
Đáp án cần chọn là: B
Đọc đoạn trích và trả lời câu hỏi dưới đây:
Làng Ku-ku-rêu của chúng tôi nằm ven chân núi, trên một cao nguyên rộng có những khe nước ào ào từ nhiều ngách đá đổ xuống. Phía dưới làng tôi là thung lũng Đất vàng, là cánh thảo nguyên Ca-dắc-xtan mênh mông nằm giữa các nhánh của rặng núi Đen và con đường sắt làm thành một dải thẫm màu băng qua đồng bằng chạy tít đến tận chân trời phía Tây. (Trích Cô bé bán diêm)
Nội dung của đoạn trích trên là gì?
Đáp án đúng là: A
Đọc đoạn trích
Đáp án cần chọn là: A
Đọc đoạn trích dưới đây và trả lời các câu hỏi từ 86 đến 90:
“Lâu nay, khái niệm trí thức thường bị hiểu thiên lệch vì nhuốm màu bằng cấp. Tôi thấy nhiều khi công chúng dùng chữ "trí thức" để chỉ người có bằng đại học trở lên. Nhưng cách hiểu đó có lẽ chưa đúng.
Có những nhóm người Việt trong và ngoài nước lấy từ "trí thức" làm tên diễn đàn, hội của họ. Vì họ cho rằng các thành viên là người có bằng cấp, một số giữ giữ các chức vụ khoa bảng, học hàm, học vị cao. Nhưng vài người trong đó chia sẻ với tôi, họ vẫn cảm thấy dè dặt tự nhận mình là trí thức. Theo họ, đó là một đại ngôn. Tuy nhiên, nếu đã hiểu ý nghĩa của khái niệm trí thức thì những người có bằng cấp cao cũng có lý do để dè dặt hơn khi tự xem mình là trí thức.
Tôi tìm hiểu, chữ "trí thức" xuất hiện lần đầu ở Việt Nam vào đầu thập niên 1930 trong cuốn Từ điển Pháp - Việt do Đào Duy Anh biên soạn. Ông dịch chữ intellectuel là "trí thức". Trí thức có thể hiểu là người làm cho xã hội lúc nào cũng thức tỉnh. Để làm cho xã hội thức tỉnh, người trí thức phải hội đủ ba yếu tố: có kiến thức, nhiều ý tưởng mới, giá trị và tự nguyện dấn thân. Tôi thấy cách dịch của cụ Đào Duy Anh rất hay và đúng. Hiểu theo nghĩa đó, người làm cho xã hội thức tỉnh không nhất thiết phải có bằng cấp đại học, thạc sĩ, tiến sĩ, giáo sư hay danh hiệu khoa bảng. Nghệ sĩ, nhà văn, nhà báo, bác sĩ, nhà giáo, nhà khoa học, nhà sư, linh mục, doanh nhân... đều có thể là trí thức. Chúng ta có thể nghĩ ngay đến những vị tiền nhân như Phan Châu Trinh, Phan Khôi, Phạm Quỳnh, Nguyễn Văn Vĩnh, Trần Quý Cáp, Huỳnh Thúc Kháng... Họ là những trí thức tiêu biểu của đất nước.”
(Trích Trí thức là ai, Nguyễn Văn Tuấn, SGK Ngữ văn lớp 12, tập 1)
Trả lời cho các câu 86, 87, 88, 89, 90 dưới đây:
Theo đoạn trích, khái niệm trí thức được dùng để chỉ đối tượng nào?
Đáp án đúng là: C
Căn cứ văn bản
Đáp án cần chọn là: C
Theo tác giả, người làm cho xã hội thức tỉnh KHÔNG cần có yếu tố nào sau đây?
Đáp án đúng là: D
Căn cứ văn bản
Đáp án cần chọn là: D
Từ “đại ngôn” (in đậm) trong đoạn trích được hiểu theo nghĩa nào?
Đáp án đúng là: D
Căn cứ nội dung bài đọc.
Đáp án cần chọn là: D
Ý nào được suy ra từ đoạn trích là chính xác?
Đáp án đúng là: C
Căn cứ nội dung bài đọc.
Đáp án cần chọn là: C
Theo lập luận của tác giả, mối quan hệ giữa “trí thức” và “bằng cấp” là gì?
Đáp án đúng là: C
Căn cứ nội dung bài đọc
Đáp án cần chọn là: C
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 91 đến 95:
“Ta đã lớn lên rồi trong khói lửa
Chúng nó chẳng còn mong được nữa
Chặn bàn chân một dân tộc anh hùng
Những bàn chân từ than bụi, lầy bùn
Đã bước dưới mặt trời cách mạng.
Những bàn chân của Hóc Môn, Ba Tơ, Cao Lạng
Lừng lẫy Điện Biên, chấn động địa cầu
Những bàn chân đã vùng dậy đạp đầu
Lũ chúa đất xuống bùn đen vạn kiếp!
Ta đi tới, trên đường ta bước tiếp,
Rắn như thép, vững như đồng.
Đội ngũ ta trùng trùng điệp điệp
Cao như núi, dài như sông
Chí ta lớn như biển Đông trước mặt!”
(Trích “Ta đi tới”, Tố Hữu)
Trả lời cho các câu 91, 92, 93, 94, 95 dưới đây:
Nêu ra phương thức biểu đạt chính được sử dụng trong đoạn thơ?
Đáp án đúng là: D
Căn cứ nội dung bài đọc
Đáp án cần chọn là: D
Nội dung chính của đoạn trích là gì?
Đáp án đúng là: C
Căn cứ nội dung bài đọc.
Đáp án cần chọn là: C
Biện pháp tu từ nghệ thuật nào được sử dụng chủ yếu trong đoạn trích sau:
“Ta đi tới, trên đường ta bước tiếp,
Rắn như thép, vững như đồng.
Đội ngũ ta trùng trùng điệp điệp
Cao như núi, dài như sông
Chí ta lớn như biển Đông trước mặt!”
Đáp án đúng là: A
Căn cứ nội dung bài đọc.
Đáp án cần chọn là: A
Biện pháp tu từ nghệ thuật trong đoạn trích trên có tác dụng gì?
Đáp án đúng là:
Căn cứ nội dung bài đọc.
Đáp án cần chọn là:
Ý nào sau đây biểu đạt ý nghĩa của câu thơ “Những bàn chân từ than bụi, lầy bùn- Đã bước dưới mặt trời cách mạng”?
Đáp án đúng là: C
Căn cứ nội dung bài đọc
Đáp án cần chọn là: C
Đọc đoạn trích dưới đây và trả lời các câu hỏi từ 96 đến 100
“Con Sông Đà tuôn dài tuôn dài như một áng tóc trữ tình, đầu tóc chân tóc ẩn hiện trong mây trời tây Bắc bung nở hoa ban hoa gạo tháng hai và cuồn cuộn mù khói Mèo đốt nương xuân. Tôi đã nhìn say sưa làn mây mùa xuân bay trên Sông Đà, tôi đã xuyên qua đám mây mùa thu mà nhìn xuống dòng nước Sông Đà. Mùa xuân dòng xanh ngọc bích, chứ nước Sông Đà không xanh màu xanh canh hến của Sông Gâm Sông Lô. Mùa thu nước Sông đà lừ lừ chín đỏ như da mặt một người bầm đi vì rượu bữa, lừ lừ cái màu đỏ giận dữ ở một người bất mãn bực bội gì mỗi độ thu về. Chưa hề bao giờ tôi thấy dòng Sông Đà là đen như thực dân Pháp đã đè ngửa con sông ta ra đổ mực Tây vào mà gọi bằng một cái tên Tây láo lếu, rồi cứ thế mà phiết vào bản đồ lai chữ.”
(Trích Người lái đò Sông Đà – Nguyễn Tuân)
Trả lời cho các câu 96, 97, 98, 99, 100 dưới đây:
Đoạn trích đã thể hiện vẻ đẹp nào của con Sông Đà?
Đáp án đúng là: B
Căn cứ nội dung bài đọc
Đáp án cần chọn là: B
Trong đoạn trích, tác giả đã sử dụng các phương thức biểu đạt chủ yếu nào?
Đáp án đúng là: A
Căn cứ nội dung bài đọc.
Đáp án cần chọn là: A
Biện pháp tu từ nghệ thuật nào được sử dụng chủ yếu trong câu sau: “Mùa xuân dòng xanh ngọc bích, chứ nước Sông Đà không xanh màu xanh canh hến của Sông Gâm Sông Lô.”?
Đáp án đúng là: A
Căn cứ nội dung bài đọc.
Đáp án cần chọn là: A
Từ “màu xanh canh hến” (in đậm) trong đoạn trích được hiểu theo nghĩa nào?
Đáp án đúng là: D
Căn cứ nội dung bài đọc.
Đáp án cần chọn là: D
Giọng điệu nổi bật của đoạn trích là gì?
Đáp án đúng là: C
Căn cứ nội dung bài đọc
Đáp án cần chọn là: C