Cho hàm số bậc ba $y = f(x)$ có đồ thị là đường cong trong hình bên
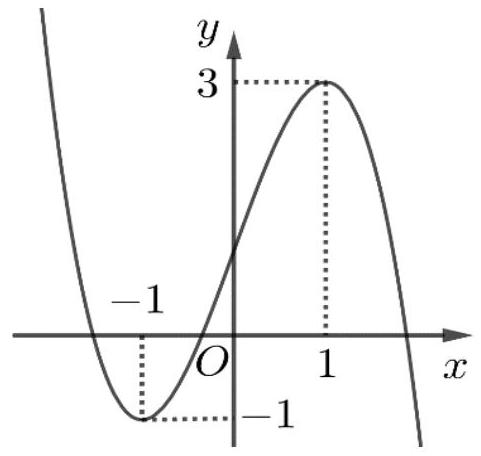
Hàm số đồng biến trên khoảng nào trong các khoảng sau đây?
Đáp án đúng là: A
Quan sát đồ thị đồng biến khi có hướng “đi lên”
Đáp án cần chọn là: A
Cho hàm số $y = f(x)$ có bảng biến thiên như sau:
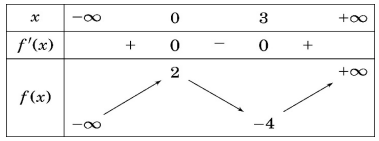
Tìm điểm cực tiểu của hàm số $y = f(x)$.
Đáp án đúng là: C
Điểm cực tiểu của hàm số khi $f'(x)$ chuyển dấu từ âm sang dương khi đi qua
Đáp án cần chọn là: C
Cho hàm số $y = f(x)$ có đồ thị như hình vẽ bên.
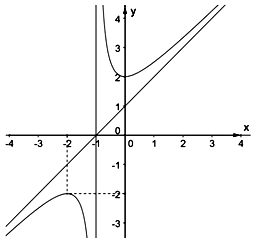
Tiệm cận đứng của đồ thị hàm số là
Đáp án đúng là: A
Quan sát đồ thị và nhận xét tiệm cận
Đáp án cần chọn là: A
Cho hàm số $y = f(x)$ có đồ thị như hình vẽ.
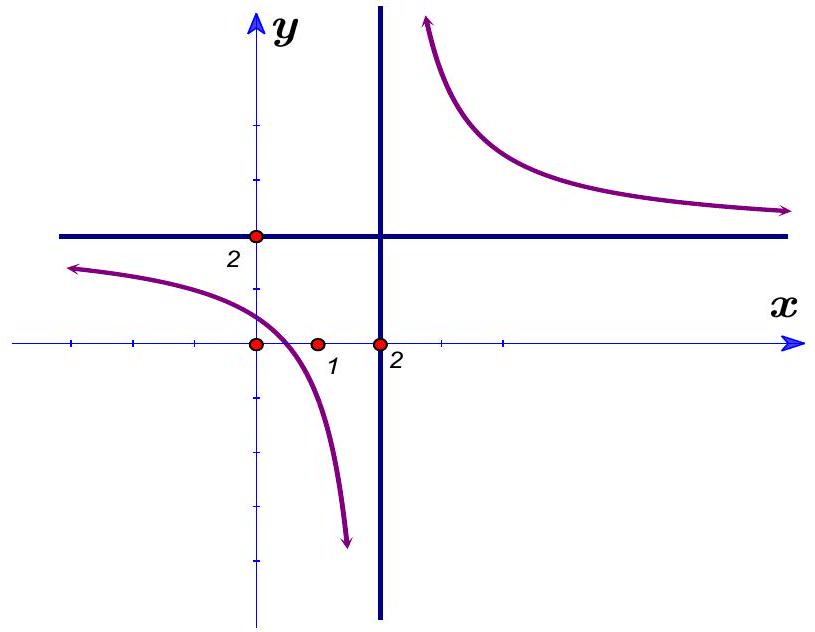
Đồ thị hàm số có tâm đối xứng là
Đáp án đúng là: B
Tâm đối xứng của đồ thị là giao của các đường tiệm cận hàm số.
Đáp án cần chọn là: B
Giá trị cực tiểu $y_{CT}$ của hàm số $y = x^{3} - 3x^{2} + 4$ là:
Đáp án đúng là: C
Bước 1: Tính đạo hàm cấp một $y'$ của hàm số.
Bước 2: Giải phương trình $y' = 0$ để tìm các điểm cực trị.
Bước 3: Sử dụng đạo hàm cấp hai $y^{''}\left( x_{0} \right) > 0$ để xác định điểm cực tiểu.
Giá trị cực tiểu là giá trị của hàm số tại điểm cực tiểu đó.
Đáp án cần chọn là: C
Cho hình lập phương $ABCD \cdot A'B'C'D'$ (hình vẽ).
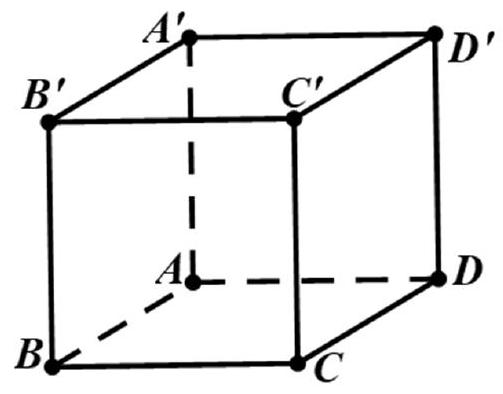
Góc giữa hai vecto $\overset{\rightarrow}{BC}$ và $\overset{\rightarrow}{B^{\prime}D^{\prime}}$ bằng:
Đáp án đúng là: D
Góc giữa hai vectơ a và b bằng góc giữa hai đường thẳng chứa chúng khi tịnh tiến chúng về cùng một điểm gốc. Ta tịnh tiến vectơ để đưa chúng về cùng một mặt phẳng.
Đáp án cần chọn là: D
Cho hàm số $y = f(x)$ có đồ thị như hình bên.
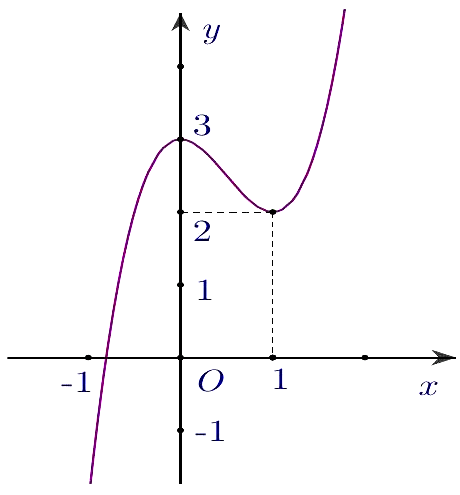
Số nghiệm của phương trình $2f(x) - 5 = 0$ là
Đáp án đúng là: C
Sử dụng tương giao đồ thị hàm số
Đáp án cần chọn là: C
Cho hình lăng trụ tam giác $ABC.A'B'C'$. Vectơ nào sau đây bằng vec tơ $\overset{\rightarrow}{AC}$ ?
Đáp án đúng là: B
Hai vecto bằng nhau khi chúng cùng hướng, cùng độ dài.
Đáp án cần chọn là: B
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên
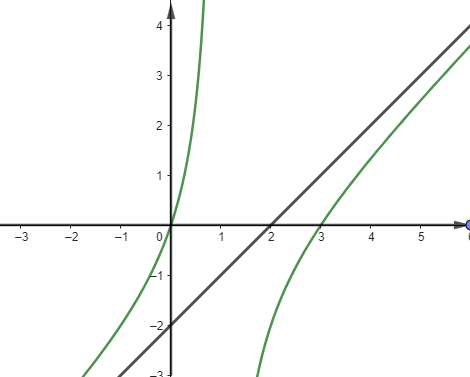
Đáp án đúng là: C
Dựa vào các đường tiệm cận để xác định hàm số
Đáp án cần chọn là: C
Hàm số $y = x^{3} - 3x - 2025$ nghịch biến trên khoảng
Đáp án đúng là: D
Tìm khoảng mà $y' \leq 0$
Đáp án cần chọn là: D
Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số $y = \dfrac{x^{2} + x + 1}{x + 1}$ là
Đáp án đúng là: A
Tính đạo hàm tìm các điểm cực trị và viết phương trình đường thẳng
Đáp án cần chọn là: A
Trong không gian với hệ tọa độ $Oxyz$, cho các vectơ $\overset{\rightarrow}{a} = \left( {3; - 1;2} \right),\overset{\rightarrow}{b} = \left( {1;4; - 2} \right)$. Tìm tọa độ của vectơ $\overset{\rightarrow}{c} = \overset{\rightarrow}{a} - 2\overset{\rightarrow}{b}$.
Đáp án đúng là: C
Phép toán vectơ: Với $a = \left( {x_{a};y_{a};z_{a}} \right)$ và $b = \left( {x_{b};y_{b};z_{b}} \right)$, vectơ $c = a - 2b$ có tọa độ là: $c = \left( {x_{a} - 2x_{b};y_{a} - 2y_{b};z_{a} - 2z_{z}} \right)$
Đáp án cần chọn là: C
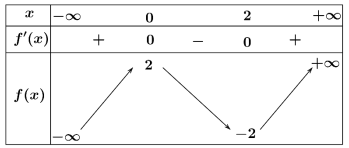
Cho hàm số $y = f(x)$ xác định và liên tục trên $\mathbb{R}$ có bảng biến thiên như hình vẽ dưới đây.
| Đúng | Sai | |
|---|---|---|
| a) Hàm số đồng biến trên khoảng $\left( {- \infty;0} \right)$ và $\left( {2; + \infty} \right)$. | ||
| b) Điểm cực đại của đồ thị hàm số hàm số là $x = 0$. | ||
| c) Tổng giá trị lớn nhất và giá trị nhỏ nhất trên đoạn $\left\lbrack {0;2} \right\rbrack$ bằng 0. | ||
| d) Giá trị nhỏ nhất của hàm số trên $\left( {2; + \infty} \right)$ bằng -2. |
Đáp án đúng là: Đ; S; Đ; S
Quan sát BBT để xác định tính đơn điệu, cực trị, GTLN, GTNN
Đáp án cần chọn là: Đ; S; Đ; S
Trong không gian $Oxyz$, cho $\Delta ABC$, biết $A\left( {3;1; - 3} \right),B\left( {4;2;0} \right),C\left( {- 1;0;3} \right)$. Các mệnh đề sau đúng hay sai?
| Đúng | Sai | |
|---|---|---|
| a) $\overset{\rightarrow}{OA} = 3\overset{\rightarrow}{i} + \overset{\rightarrow}{j} + 3\overset{\rightarrow}{k}$. | ||
| b) $G\left( {2;1;0} \right)$ là trọng tâm tam giác $ABC$. | ||
| c) Hình chiếu của $C$ lên $Ox$ là $C'\left( {- 1;0;0} \right)$. | ||
| d) Khoảng cách giữa 2 điểm $A$ và $B$ bằng $\sqrt{8}$. |
Đáp án đúng là: S; Đ; Đ; S
a) Quan sát hệ số của $\overset{\rightarrow}{i};\overset{\rightarrow}{j};\overset{\rightarrow}{k}$
b) Toạ độ G thoả mãn $x_{G} = \dfrac{x_{A} + x_{B} + x_{C}}{3};y_{G} = \dfrac{y_{A} + y_{B} + y_{C}}{3};z_{G} = \dfrac{z_{A} + z_{B} + z_{C}}{3}$
c) Hình chiếu $M\left( {x,y,z} \right)$ lên Ox là $M'\left( {x;0;0} \right)$
d) $\overset{\rightarrow}{AB} = \left( {x_{B} - x_{A};y_{B} - y_{A};z_{B} - z_{A}} \right)$. Khi đó $\left| \overset{\rightarrow}{AB} \right| = \sqrt{\left( {x_{B} - x_{A}} \right)^{2} + \left( {y_{B} - y_{A}} \right)^{2} + \left( {z_{B} - z_{A}} \right)^{2}}$
Đáp án cần chọn là: S; Đ; Đ; S
Cho hàm số bậc ba $y = f(x) = \dfrac{ax^{2} + bx + c}{mx + n}\ \left( {x \neq \dfrac{- n}{m}} \right)$ có đồ thị như hình vẽ
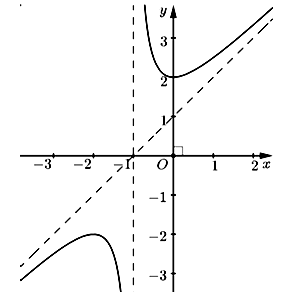
Khi đó:
| Đúng | Sai | |
|---|---|---|
| a) Hàm số đạt cực tiểu tại $x = 2$. | ||
| b) Phương trình tiệm cận xiên của đồ thị hàm số là $y = x + 1$. | ||
| c) Giá trị nhỏ nhất của hàm số trên khoảng $\left( {- \infty;0} \right)$ là 2 | ||
| d) Hàm số nghịch biến trên khoảng $\left( {- 1;0} \right)$. |
Đáp án đúng là: S; Đ; S; Đ
Quan sát đồ thị để xác định các khoảng đơn điệu, cực trị, GTLN, GTNN và các đường tiệm cận.
Đáp án cần chọn là: S; Đ; S; Đ
Trong không gian $Oxyz$, vị trí của điểm $M$ như hình vẽ. Gọi $H$ là hình chiếc vuông góc của $M$ xuống mặt phẳng $\left( {Oxy} \right)$. Cho biết $AH = 12,\left( {\overset{\rightarrow}{i},\overset{\rightarrow}{OH}} \right) = 30^{\circ},\left( {\overset{\rightarrow}{OH},\overset{\rightarrow}{OM}} \right) = 60^{\circ}$.
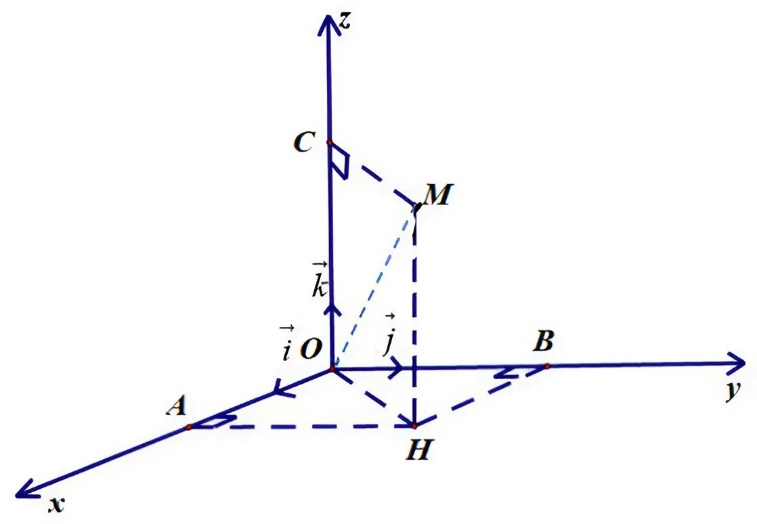
Các mệnh đề sau đúng hay sai?
| Đúng | Sai | |
|---|---|---|
| a) Tọa độ của điểm $A$ là $\left( {12\sqrt{3};0;0} \right)$. | ||
| b) Tọa độ của điểm $B$ là $\left( {12;0;0} \right)$. | ||
| c) $OC = OM \cdot \text{sin}\widehat{HOM}$. | ||
| d) Tọa độ của điểm $M$ là $\left( {12\sqrt{3};12;48\sqrt{3}} \right)$. |
Đáp án đúng là: Đ; S; Đ; S
Dựa vào tam giác vuông và góc tính độ dài OM, OA, OB, OC
Đáp án cần chọn là: Đ; S; Đ; S
Biết đồ thị hàm số $y = \dfrac{x^{2} + 3x + 2}{x - 3}$ có đường tiệm cận xiên $y = g(x) = ax + b$. Tính $g\left( {- 2} \right)$.
Đáp án đúng là:
Chia tử số cho mẫu số tìm TCX
Đáp án cần điền là: 4
Giả sử giá trị nhỏ nhất của hàm số $y = \dfrac{\text{ln}x}{x}$ trên đoạn $\left\lbrack {2;3} \right\rbrack$ bằng $\dfrac{a \cdot \text{ln}2}{b}$ với $\text{a},\text{b}$ nguyên tố cùng nhau. Tính $a - 5b$
Đáp án đúng là:
Tính đạo hàm, giải phương trình $y' = 0$ và tính giá trị của hàm số trên $\left\lbrack {2;3} \right\rbrack$
Đáp án cần điền là: -9
Trong không gian $Oxyz$, cho hình chóp $S.ABCD$ có đáy là hình thang vuông tại $A$ và $D$. Điểm $A$ trùng với gốc tọa độ $O,S\left( {0;0;3\sqrt{2}} \right),B\left( {0;4;0} \right),C\left( {3;2;0} \right)$ (như hình vẽ). Gọi $G$ là trọng tâm của tam giác $SBC$. Tính cosin của góc giữa hai vectơ $\overset{\rightarrow}{AG}$ và $\overset{\rightarrow}{BD}$ (kết quả làm tròn đến hàng phần chục).
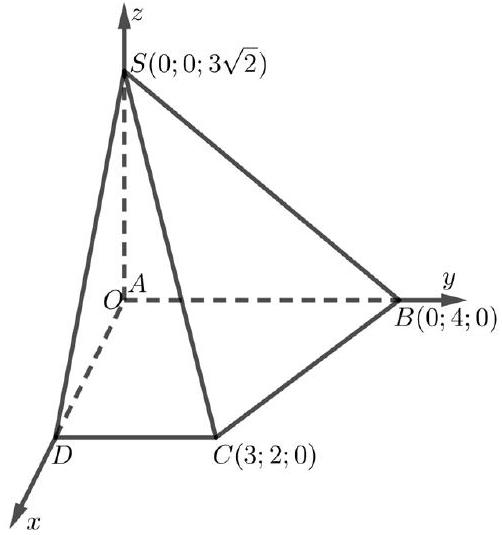
Đáp án đúng là:
$ABCD$ là hình thang vuông tại $A$ và $D$ tìm toạ độ D
Toạ độ G làm trọng tâm $\Delta ABC$ thoả mãn $x_{G} = \dfrac{x_{A} + x_{B} + x_{C}}{3};y_{G} = \dfrac{y_{A} + y_{B} + y_{C}}{3};z_{G} = \dfrac{z_{A} + z_{B} + z_{C}}{3}$
$\text{cos}\left( {\overset{\rightarrow}{AG};\overset{\rightarrow}{BD}} \right) = \dfrac{\overset{\rightarrow}{AG}.\overset{\rightarrow}{BD}}{AG.BD}$
Đáp án cần điền là: -0,4
Trong không gian với hệ trục tọa độ $Oxyz$ cho hình thang $ABCD$ vuông tại $A$ và $B$. Ba đỉnh $A\left( {1;2;1} \right),B\left( {2;0; - 1} \right),C\left( {6;1;0} \right)$ Hình thang có diện tích bằng $6\sqrt{2}$. Giả sử đỉnh $D\left( {a;b;c} \right)$. Tìm $a + b + c$ ?
Đáp án đúng là:
Từ $\left. AD \parallel BC\Rightarrow\overset{\rightarrow}{AD} = k\overset{\rightarrow}{BC} \right.$ với $k > 0$ gọi D theo tham số k
$S_{ABCD} = \dfrac{1}{2}AB\left( {AD + BC} \right) = 6\sqrt{2}$ tính độ dài AD từ đó tìm k và toạ độ D.
Đáp án cần điền là: 6
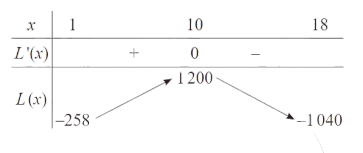
Một hộ làm nghề dệt vải lụa tơ tằm sán xuất mổi ngày được $x$ mét vải lụa ( $1 \leq x \leq 18$ ).
Tống chi phí sản xuất $x$ mét vải lụa, tính bằng nghìn đồng, cho bởi hàm chi phí:
$$ C(x)=x^3-3 x^2-20 x+500 $$
Giả sử hộ làm nghề dệt này bán hết sản phấm mỗi ngày với giá 220 nghìn đồng/mét. Gọi $B(x)$ là số tiền bán được và $L(x)$ là lọ̣i nhuận thu được khi bán $x$ mét vái lụa. Hộ làm nghề dệt này cần sán xuất và bán ra mỗi ngày bao nhiêu mét vải lụa đế thu được lợi nhuận tối đa. Hãy tính lợi nhuận tối đa đó (đơn vị: nghìn đồng)
Đáp án đúng là:
Đáp án cần điền là: 1200
Giả sử số lượng tế bào của một quần thể nấm men tại môi trường nuôi cấy trong phòng thí nghiệm được mô hình hoá bằng hàm số $P(t) = \dfrac{a}{b + e^{- 0,75t}}(a,b \in {\mathbb{R}})$, trong đó thời gian $t$ được tính bằng giờ. Đạo hàm của hàm số $y = P(t)$ biểu thị tốc độ sinh trưởng của nấm men (tính bằng tế bào /giờ) tại thời điểm t (giờ). Tại thời điểm ban đầu $t = 0$, quần thể có 20 tế bào và tốc độ sinh trường là 10 tế bào/giờ. Tìm số lượng tế bào của quần thể nấm men tại thời điểm tốc độ sinh trường của quần thể đạt mức tối đa.
Đáp án đúng là:
Tính $P'(t)$. Từ $\left\{ \begin{array}{l} {P(0) = 20} \\ {P'(0) = 10} \end{array} \right.$ xác định a, b
Khảo sát hàm số tìm GTLN của $P'(t)$ đạt tại $t_{0}$. Khi đó số lượng tế bào là $P\left( t_{0} \right)$
Đáp án cần điền là: 30