Phần 1: Tư duy Toán học
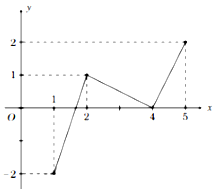
Cho hàm số \(y = f\left( x \right)\) có đồ thị trên đoạn \(\left[ {1;\,\,5} \right]\) như hình vẽ. Chọn các khẳng định đúng
Đáp án đúng là: C; D
Đáp án cần chọn là: C; D
Tập nghiệm của phương trình \({\log _2}\left( {{x^2} - 4x + 1} \right) = {\log _2}\left( {x - 3} \right)\) là
Đáp án đúng là: D
- Tìm ĐKXĐ
- Giải phương trình
Đáp án cần chọn là: D
Nếu \(\int\limits_0^2 {f\left( x \right)dx} = 4\) thì \(\int\limits_0^2 {\left[ {\dfrac{1}{2}f\left( x \right) + 3} \right]} dx\) bằng
Đáp án đúng là: C
Tính tích phân
Đáp án cần chọn là: C
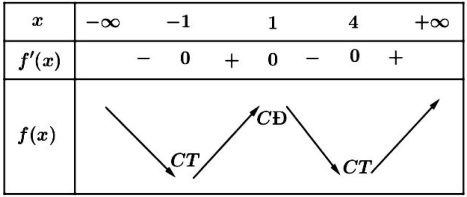
Cho hàm số \(y=f(x)\) có đạo hàm liên tục trên \(\mathbb{R}\). Hàm số \(y=f^{\prime}(x)\) có đồ thị như hình dưới đây. Xét tính đúng sai của các khẳng định sau:
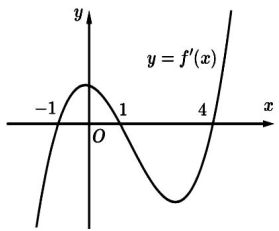
| Đúng | Sai | |
|---|---|---|
| a) Hàm số \(y=f(x)\) có hai cực trị |
||
| b) Hàm số \(y=f(x)\) đồng biến trên khoảng \((1 ;+\infty)\) |
||
| c) \(f(1)>f(2)>f(4)\) |
||
| d) Trên đoạn \([-1 ; 4]\) thì giá trị lớn nhất của hàm số \(y=f(x)\) là \(f(1)\). |
Đáp án đúng là: S; S; Đ; Đ
Đáp án cần chọn là: S; S; Đ; Đ
Cho hai mặt phẳng \(\left( P \right),\,\,\left( Q \right)\) song song và cùng tiếp xúc với mặt cầu \(S\left( {O;2R} \right)\). Gọi \(d\) là khoảng cách giữa \(\left( P \right)\) và \(\left( Q \right)\). Tìm \(d\) biết \(R = 2\)
Đáp án đúng là: B
Cho hai mặt phẳng \(({\rm{P}})\) và \(({\rm{Q}})\) song song với nhau. Khoảng cách giữa mặt phẳng \(({\rm{P}})\) và \((Q)\) là khoảng cách từ một điểm \(M\) bất kỳ trên mặt phẳng \((P)\) đến mặt phẳng \((Q)\) hoặc ngược lại. Ký hiệu là \(d((P),(Q))\).
Hai mặt phẳng \(({\rm{P}})\) và \(({\rm{Q}})\) song song với nhau và cùng tiếp xúc với mặt cầu thì khoảng cách giữa hai mặt phẳng bằng 2 lần bán kính của mặt cầu đó.
Đáp án cần chọn là: B
Kéo thả đáp án vào ô trống
Trên một bảng quảng cáo, người ta mắc hai hệ thống bóng đèn. Hệ thống I gồm 2 bóng mắc nối tiếp, hệ thống II gồm 2 bóng mắc song song. Khả năng bị hỏng của mỗi bóng đèn sau 6 giờ thắp sáng liên tục là 0,15. Biết tình trạng của mỗi bóng đèn là độc lập. Khi đó xác suất để
a) Hệ thống II bị hỏng (không sáng) bằng
b) Hệ thống II hoạt động bình thường bằng
c) Hệ thống I bị hỏng (không sáng) bằng
d) Cả hai hệ thống bị hỏng (không sáng) bằng
Đáp án đúng là: 0,0225; 0,9775; 0,2775; 0,3
Đáp án cần chọn là: 0,0225; 0,9775; 0,2775; 0,3
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {x - 2} \right){\left( {1 - x} \right)^2}\) với mọi \(x \in \mathbb{R}\). Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Đáp án đúng là: D
Giải phương trình \(f'\left( x \right) \ge 0\)
Đáp án cần chọn là: D
Số máy tính bán được trong 7 tháng liên tiếp của một cửa hàng được ghi lại trong bảng sau:

Xét tính đúng sai của các mệnh đề:
| Đúng | Sai | |
|---|---|---|
| a) Khoảng biến thiên và khoảng tứ phân vị lần lượt là 20 và 12. | ||
| b) Số trung bình: \(\bar{x} = \dfrac{551}{7}\). | ||
| c) Phương sai của mẫu số liệu là \(s^2 =58,55.\) | ||
| d) Độ lệch chuẩn: \(s=\sqrt{50,63}\) |
Đáp án đúng là: S; Đ; Đ; S
Đáp án cần chọn là: S; Đ; Đ; S
Với \(b\) là số thực dương và \(\alpha \) là số thực thỏa mãn \({b^\alpha } + {b^{ - \alpha }} = 3\). Giá trị của \({b^{2\alpha }} + {b^{ - 2\alpha }}\) bằng
Đáp án đúng là: A
Bình phương hai vế của giả thiết.
Đáp án cần chọn là: A
Trong không gian \(Oxyz\), mặt phẳng \(\left( P \right):\dfrac{x}{2} + \dfrac{y}{3} - \dfrac{z}{3} + 1 = 0\) có một vec tơ pháp tuyến là
Đáp án đúng là: A
Vec tơ pháp tuyến của \(\left( P \right):ax + by + cz + d = 0\) là \(\overrightarrow {{n_P}} = \left( {a;b;c} \right)\)
Đáp án cần chọn là: A
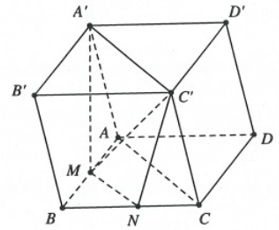
Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \(M\) là trung điểm của \(AB\), mặt phẳng \(\left( {MA'C'} \right)\) cắt cạnh \(BC\) tại \(N\). Tỉ số \(\dfrac{{MN}}{{A'C'}}\) là (Viết kết quả dưới dạng số thập phân)
Đáp án đúng là: 0,5
Sử dụng tính chất của hai mặt phẳng song song
Đáp án cần điền là: 0,5
Một hộp chứa 11 quả cầu được đánh số từ 1 đến 11. Lấy ngẫu nhiên bốn quả từ hộp đó, xác suất để tổng bốn số ghi trên chúng là số chẵn bằng
Đáp án đúng là: B
Chia 11 số thành 2 tập số chẵn và số lẻ
Đáp án cần chọn là: B
Người ta tiến hành phỏng vấn 30 người về một bộ phim mới chiếu trên truyền hình. Người điểu tra yêu cầu cho điểm bộ phim trên thang điểm là 100. Kết quả được trình bày trong bảng phân bố tần số ghép lớp sau đây:

Mốt của mẫu số liệu là: (Làm tròn đến hàng phần mười)
Đáp án đúng là: 76,7
Để tìm mốt của mẫu số liệu ghép nhóm, ta thực hiện theo các bước sau:
Bước 1. Xác định nhóm có tần số lớn nhất (gọi là nhóm chứa mốt), giả sử là nhóm j: \(\left[ {{a_j};{a_{j + 1}}} \right)\).
Bước 2. Mốt được xác định là: \({M_o} = {a_j} + \dfrac{{{m_j} - {m_{j - 1}}}}{{\left( {{m_j} - {m_{j - 1}}} \right) + \left( {{m_j} - {m_{j - 1}}} \right)}} \cdot h\)
trong đó \({m_j}\) là tần số của nhóm \(j\) (quy ước \({m_0} = {m_{k + 1}} = 0\) ) và \(h\) là độ dài của nhóm.
Đáp án cần điền là: 76,7
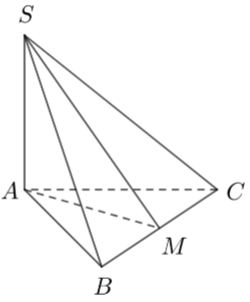
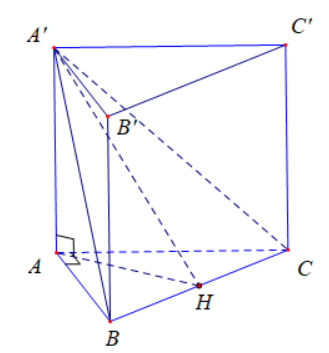
Cho hình chóp \(S.ABC\) có đáy là tam giác đều cạnh bằng \(2a\sqrt 3 \), biết \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\) và \(SA = 3a\). Góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\) bằng
Đáp án đúng là: A
Dựng góc giữa \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\).
Đáp án cần chọn là: A
Cho tập hợp \(A\) gồm 16 phần tử. Số tập con có 2 phần tử của \(A\) là
Đáp án đúng là: D
Số tập con có 2 phần tử bằng số cách chọn 2 phần tử thuộc tập \(A\)
Đáp án cần chọn là: D
Mỗi khẳng định sau đúng hay sai?
| Đúng | Sai | |
|---|---|---|
| a) Tập xác định của hàm \(y = \tan x\) là \(\left( {0, + \infty } \right)\) |
||
| b) Giá trị nhỏ nhất của hàm số \(y = 2\sin 2x\) là 0 |
||
| c) Phương trình \(\cos 2x = \cos m\) có nghiệm khi \(m \in \left[ { - 1,1} \right]\) |
||
| d) \(\sin x = 1 \Leftrightarrow x = \dfrac{\pi }{2} + k\pi {\rm{, }}k \in \mathbb{Z}{\rm{. }}\) |
Đáp án đúng là: S; S; S; S
Đáp án cần chọn là: S; S; S; S
Trong không gian \(Oxyz\), cho \(A\left( {2; - 1;2} \right)\) và \(B\left( {2;0;1} \right)\). Góc giữa đường thẳng \(AB\) và trục \(Oz\) bằng
Đáp án đúng là: C
Góc giữa hai đường thẳng trong không gian
Đáp án cần chọn là: C
Cho khối tứ diện đều có cạnh bằng \(2\sqrt 2 \). Thể tích của khối tứ diện đều đã cho bằng
Đáp án đúng là: D
Thể tích của khối tứ diện đều có cạnh \(a\) là \(V = \dfrac{{{a^3}\sqrt 2 }}{{12}}\).
Đáp án cần chọn là: D
Cho cấp số nhân \(\left( {{u_n}} \right)\) với số hạng \({u_k} = 8,\,\,{u_1} = \sqrt 2 \) và công bội \(q = \sqrt 2 \). Giá trị của \(k\) bằng
Đáp án đúng là: B
Cho cấp số nhân \(\left( {{u_n}} \right)\) với số hạng \({u_1}\) và công bội \(q\). Khi đó \({u_n} = {u_1}.{q^{n - 1}}\)
Đáp án cần chọn là: B
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vê.
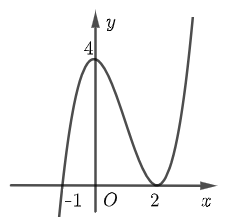
Số nghiệm thực của phương trình \(\dfrac{{f\left( {f\left( x \right)} \right)}}{{{f^2}\left( x \right) + f\left( x \right)}} = 0\) là
Đáp án đúng là: 3
Dùng tương giao đồ thị hàm số biện luận số nghiệm của phương trình.
Đáp án cần điền là: 3
Diện tích \(S\) của hình thang cong giới hạn bởi đồ thị hàm số \(y = f\left( x \right) = x\), trục hoành và hai đường thẳng \(x = 2,\,x = 4\) là
Đáp án đúng là: D
Đáp án cần chọn là: D
Cho \(a\) là số thực dương thỏa mãn \({\log _2}\left( {{{\log }_4}a} \right) = {\log _4}\left( {{{\log }_2}a} \right) + 3\). Giá trị của \({\log _2}a\) bằng
Đáp án đúng là: A
Sử dụng tính chất của hàm số logarit
Đáp án cần chọn là: A
Tích chọn các khẳng định đúng
Đáp án đúng là: B; C
Kiểm tra tính đúng sai của mệnh đề
Đáp án cần chọn là: B; C
Kéo thả đáp án vào ô trống
Cho hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị là đường cong trong hình bên dưới.
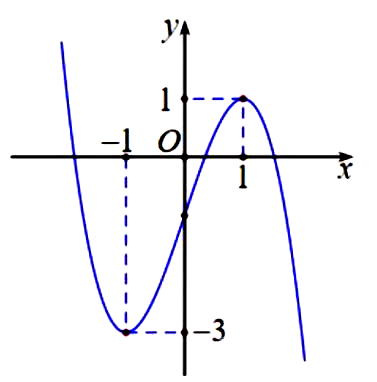
Khi đó \(b\) = , \(c\) = và \(T = f\left( {a - b + c - d - 3} \right)\) =
Đáp án đúng là: 0; 3; -1
Từ đồ thị hàm số, xác định các điểm mà đồ thị đi qua, cực đại, cực tiểu từ đó đưa về hệ phương trình tìm a,b,c,d
Đáp án cần chọn là: 0; 3; -1
Một cabin cáp treo xuất phát từ điểm \(A\left( {10;3;0} \right)\) và chuyển động đều theo đường cáp có vectơ chỉ phương là \(\vec u = \left( {2; - 2;1} \right)\) với tốc độ là \(4,5\left( {m/s} \right)\) (đơn vị trên mỗi trục tọa độ là mét) được mô hình hóa như các hình vẽ sau:
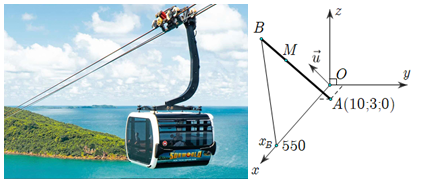
| Đúng | Sai | |
|---|---|---|
| a) Phương trình chính tắc của đường cáp là \(\dfrac{{x - 10}}{2} = \dfrac{{y - 3}}{{ - 2}} = \dfrac{z}{1}\) | ||
| b) Giả sử sau \(t\) giây kể từ lúc xuất phát \(\left( {t \ge 0} \right)\), cabin đến vị trí điểm \(M\). Khi đó tọa độ của điểm \(M\) là \(\left( {3t + 10; - 3t + 3;\dfrac{{3t}}{2}} \right)\) | ||
| c) Cabin dừng ở điểm \(B\) có hoành độ \({x_B} = 550\). Quãng đường \(AB\) có độ dài bằng \(810\left( m \right)\) (làm tròn kết quả đến hàng đơn vị của mét) | ||
| d) Đường cáp \(AB\) tạo với mặt \(\left( {Oxy} \right)\) một góc \(22^\circ \) (làm tròn đến hàng đơn vị của độ) |
Đáp án đúng là: Đ; Đ; Đ; S
Đáp án cần chọn là: Đ; Đ; Đ; S
Trong không gian, một cabin cáp treo xuất phát từ điểm \(A(-3 ; 1 ; 6)\) và chuyển động đều theo đường cáp có vecto chỉ phương là \(\vec{u}=(1 ;-2 ; 6)\) với tốc độ là 6 \(\mathrm{m} / \mathrm{s}\) (đơn vị trên mỗi trục tọa độ là mét). Giả sử sau 8 (s) kể từ lúc xuất phát, cabin đến điểm \(B\). Gọi tọa độ \(B(a ; b ; c)\). Tính \(a+b+c\), kết quả làm tròn đến hàng phần mười.
Đáp án đúng là: 41,5
Đáp án cần điền là: 41,5
Cho hàm số \(y = f(x) = 4x - \sqrt {{x^2} + 6x - 3} \) (C). Một trong hai tiệm cận xiên của \((C)\) có dạng \({\Delta _1}:y = {a_1}x + {b_1}\left( {{a_1} < 4} \right)\). Tìm \(T = a_1^{2025} + b_1^{2025}\)
Đáp án đúng là: 0
Đáp án cần điền là: 0
Trong không gian \(Oxyz\) cho các điểm \(A\left( {2;0;0} \right),B\left( {0;4;0} \right),C\left( {0;0;6} \right),D\left( {2;4;6} \right)\). Gọi \(\left( P \right)\)là mặt phẳng song song với mặt phẳng \(\left( {ABC} \right)\),\(\left( P \right)\) cách đều \(D\) và mặt phẳng \(\left( {ABC} \right)\). Phương trình của mặt phẳng \(\left( P \right)\) là \(ax + by + 2z + d = 0\) với \(a,b,d \in \mathbb{Z}\). Giá trị của \(d\) bằng bao nhiêu?
Đáp án đúng là: -24
Sử dụng công thức khoảng cách từ một điểm đến một mặt phẳng
Đáp án cần điền là: -24
Trong không gian \(Oxyz\), cho hai mặt phẳng \(\left( P \right):2x + 2y - z + 3 = 0,\)\(\left( Q \right):x + 2y - 2z + 4 = 0\) và điểm \(A\left( {1\,;\,2\,;\,3} \right)\). Xét tính đúng sai của các khẳng định sau:
| Đúng | Sai | |
|---|---|---|
| a) Điểm \(A\) cách mặt phẳng \(\left( P \right)\) một khoảng bằng \(5\). |
||
| b) Mặt phẳng \(\left( Q \right)\) cắt mặt phẳng \(\left( P \right)\). | ||
| c) Mặt phẳng \(\left( R \right):2x + 2y - z = 0\) cách mặt phẳng \(\left( P \right)\) một khoảng bằng 3. | ||
| d) Với mọi giá trị m thì hai mặt phẳng \(\left( P \right)\)và \(\left( T \right):x + y + mz + 1 = 0\) cắt nhau. |
Đáp án đúng là: S; Đ; S; S
Đáp án cần chọn là: S; Đ; S; S
Kéo thả đáp án vào ô trống
Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có tọa độ đỉnh \(A(2 ; 0 ; 0)\), \(B(0 ; 4 ; 0), C(0 ; 0 ; 6), A(2 ; 4 ; 6)\). Gọi \((S)\) là mặt cầu ngoại tiếp tứ diện ABCD. Phương trình mặt cầu \(\left(S^{\prime}\right)\) có tâm trùng với tâm của mặt cầu \((S)\) và có bán kính gấp 2 lần bán kính của mặt cầu \((S)\). Gọi phương trình mặt cầu \((S)\) có dạng: \(x^2+y^2+z^2-2 a x-2 b y-2 c z+d=0\). Khi đó \(a\) = , \(b\) = , \(d\) =
Đáp án đúng là: 1; 2; 0
Thay toạ độ các điểm \(A(2 ; 0 ; 0)\), \(B(0 ; 4 ; 0), C(0 ; 0 ; 6), A(2 ; 4 ; 6)\) vào phương trình mặt cầu giải hệ phương trình tìm các hệ số $a,b,c,d$
Đáp án cần chọn là: 1; 2; 0
Một đàn côn trùng, ở ngày thứ \(t\) có số lượng là \(K\left( t \right)\). Biết \(K'\left( t \right) = \dfrac{{4000}}{{1 + \dfrac{t}{2}}}\) và ban đầu đàn côn trùng có \(50.000\) con. Hỏi sau \(10\) ngày thì đàn có khoảng bao nhiêu con? (làm tròn kết quả đến hàng đơn vị).
Đáp án đúng là: 64334
Đáp án cần điền là: 64334
Hằng ngày, mực nước của con kênh lên xuống theo thủy triều. Độ sâu \(h\left( m \right)\)của mực nước trong kênh tính theo thời gian \(t\left( h \right)\)được cho bởi công thức \(h = 3\cos \left( {\dfrac{{\pi t}}{6} + \dfrac{\pi }{3}} \right) + 12\).
Khi nào mực nước của kênh là cao nhất với thời gian ngắn nhất?
Đáp án đúng là: 10
Tìm GTLN,GTNN của hàm số \(h = 3\cos \left( {\dfrac{{\pi t}}{6} + \dfrac{\pi }{3}} \right) + 12\) và tìm t khi hàm số đạt GTLN.
Đáp án cần điền là: 10
Cho dãy số \(\left( {{u_n}} \right)\), được xác định bởi \(\left\{ \begin{array}{l}{u_1} = - 2\\{u_{n + 1}} = - 2 - \dfrac{1}{{{u_n}}}\end{array} \right.\). Khi đó \(u_{99}=\dfrac{a}{b}\) thì \(a+b\) bằng?
Đáp án đúng là: -1
Tính \(u_1,u_2,u_3\) từ đó suy ra công thức tổng quát
Đáp án cần điền là: -1
Kéo thả đáp án vào ô trống
Trong \(45\) học sinh làm bài kiểm tra không có ai bị điểm dưới \(2\) và chỉ có \(2\) học sinh được \(10.\) Khi đó có ít nhất học sinh có điểm kiểm tra bằng nhau (điểm kiểm tra là một số tự nhiên từ \(0\) đến \(10\)).
Đáp án đúng là: 6
- Sử dụng nguyên lý Dirichlet cơ bản: Nếu nhốt \(n\) thỏ vào \(m\) lồng, với \(n > m,\) nghĩa là số thỏ nhiều hơn số lồng, thì ít nhất cũng có một lồng nhốt không ít hơn hai con thỏ.
- Phân tích: Ta coi học sinh như các con thỏ, ta lập được các cái lồng là các lồng chứa những học sinh có cùng số điểm ở bài kiểm tra.
Đáp án cần chọn là: 6
Người ta cần sản xuất một chiếc cốc thủy tính có dạng hình trụ không có nắp với đáy cốc và thành cốc làm bằng thủy tinh đặc, phần đáy cốc dày đều 1,5cm và thành xung quanh cốc dày đều 0,2cm (tham khảo hình vẽ bên). Biết rằng chiều cao của chiếc cốc là 15cm và khi ta đổ 180ml nước vào cốc thì đầy cốc. Tính thể tích thủy tinh để sản xuất chiếc cốc đó, làm tròn đến hàng phần trăm.
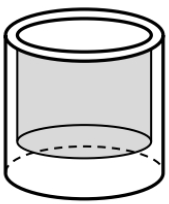
Đáp án đúng là: D
Thể tích hình trụ có chiều cao h, bán kính đáy r là: \(V = \pi {r^2}h\).
Từ thể nước trong cốc tính bán kính của cốc thuỷ tính từ đó tính phần thể tích cần dùng để sản xuất chiếc cốc.
Đáp án cần chọn là: D
Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích mặt trên của mỗi tầng bằng nửa diện tích mặt trên của tầng ngay bên dưới và diện tích mặt trên của tằng 1 bằng nửa diện tích của đế tháp (có diện tích là \(12288\;{{\rm{m}}^2}\) ). Diện tích mặt trên cùng (của tầng thứ 11) có giá trị nào sau đây?

Đáp án đúng là: 6
Sử dụng công thức cấp số nhân
Đáp án cần điền là: 6
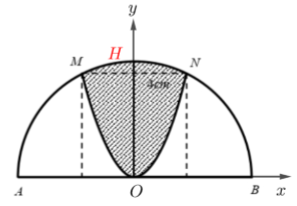
Cho nửa đường tròn đường kính \(AB = 4\sqrt 5 \). Trên đó người ta vẽ một parabol có đỉnh trùng với tâm của nửa hình tròn, trục đối xứng là đường kính vuông góc với \(AB\). Parabol cắt nửa đường tròn tại hai điểm \(M,\,\,N\) với \(MN = 4cm\). Sau đó người ta cắt bỏ phần hình phẳng giới hạn bởi đường tròn và parabol (phần gạch chéo trong hình vẽ). Đem phần còn lại quay xung quanh trục \(AB\). Thể tích của khối tròn xoay thu được bằng
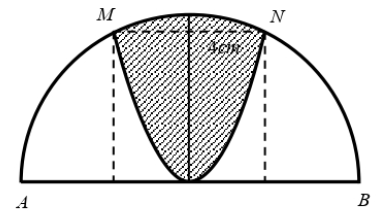
Đáp án đúng là: A
Đáp án cần chọn là: A
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\)là tam giác vuông cân tại \(A,\,AB = a\). Biết góc giữa hai mặt phẳng \(\left( {A'BC} \right)\) và \(\left( {ABC} \right)\) bằng \(30^\circ \), thể tích của khối lăng trụ đã cho bằng.
Đáp án đúng là: A
Đáp án cần chọn là: A
Nếu \(p \ge 5\) và \(2p + 1\) là các số nguyên tố thì
| Đúng | Sai | |
|---|---|---|
| a) \(6p + 2\) là số nguyên tố | ||
| b) \(4p + 1\) là số nguyên tố |
Đáp án đúng là: S; S
Đáp án cần chọn là: S; S
Dãy Fibonacci \(\left( {{F_n}} \right)\) mang tên chính nhà toán hoc Pisano Fibonacci. Dãy cho bởi hệ thức truy hồi đơn giản \(\left\{ {\begin{array}{*{20}{l}}{{F_1} = {F_2} = 1}\\{{F_{n + 2}} = {F_{n + 1}} + {F_n}\quad \forall n \ge 1}\end{array}} \right.\). Dùng phương pháp xác định số hạng tổng quát của dãy số bằng phương trình đặc trưng thấy công thức tổng quát của dãy \(\left( {{F_n}} \right)\) là: \({F_n} = \dfrac{1}{{\sqrt 5 }}\left[ {{{\left( {\dfrac{{1 + \sqrt 5 }}{2}} \right)}^n} - {{\left( {\dfrac{{1 - \sqrt 5 }}{2}} \right)}^n}} \right]\). Khi đó ứng dụng dãy này để giải quyết bài toán sau:
Cho phép sử dụng hai loại gạch có kích thước 1×1 và 1×2. Khi đó có bao nhiêu cách khác nhau để dùng hai loại gạch này xếp thành một hình chữ nhật có kích thước 1×20?
Đáp án đúng là: 10946
a) Viết 10 số hạng đầu của dãy và tính tổng
b) Đưa bài toán về dãy Fib0nacci
Đáp án cần điền là: 10946
Phần 2: Tư duy đọc hiểu
Đọc văn bản sau và trả lời các câu hỏi:
ĐỊA NHIỆT
[1] Việt Nam có tiềm năng địa nhiệt đáng kể và có thể phát triển các nhà máy điện địa nhiệt. Điều này sẽ mang lại một nguồn năng lượng mới, những cơ hội mới, nâng cao năng lực, trình độ cho các nhà khoa học, tạo ra nhiều công ăn việc làm và góp phần xây dựng nền kinh tế xanh mà Việt Nam đang hướng đến.
[2] Năng lượng địa nhiệt là năng lượng được tách ra từ nhiệt trong lòng Trái Đất. Năng lượng này có nguồn gốc từ sự hình thành ban đầu của hành tinh, từ hoạt động phân hủy phóng xạ của các khoáng vật và từ năng lượng mặt trời được hấp thụ tại bề mặt Trái đất. Nguồn địa nhiệt bản thân không thể giải quyết được căn bản các vấn đề năng lượng nhưng góp phần giảm bớt sự phụ thuộc vào sử dụng nhiên liệu hóa thạch. Loại năng lượng này đã được khai thác và sử dụng từ những năm đầu thế kỷ 20 cho mục đích sưởi ấm, sấy nông sản, tắm thư giãn… Đến nay, việc nghiên cứu và phát triển công nghệ khai thác nguồn năng lượng địa nhiệt ngày càng phát triển nhanh về quy mô và hiệu suất. Các nhà máy sản xuất điện từ địa nhiệt (cho giá thành rẻ và sạch về sinh thái) đã được xây dựng tương đối phổ biến tại nhiều quốc gia như Mỹ, Trung Quốc, Pháp, New Zealand, Nhật, Philippines, Canada, Úc…
[3] Ông Tạ Văn Hường - Chủ tịch Hiệp hội Năng lượng sạch Việt Nam nhận định: Nước ta được đánh giá là có tiềm năng địa nhiệt trung bình so với thế giới. Nguồn năng lượng này ở nước ta còn có ưu điểm là phân bổ đều trên khắp lãnh thổ cả nước nên cho phép sử dụng rộng rãi ở hầu hết các địa phương. Mặc dù còn nhiều thách thức về kinh tế, kỹ thuật, nguồn vốn đầu tư… nhưng việc khai thác địa nhiệt tại Việt Nam đã và sẽ mở ra triển vọng khai thác, ứng dụng nguồn năng lượng hữu ích này rộng rãi vào đời sống kinh tế xã hội của đất nước, vừa giải quyết được bài toán kinh tế vừa thân thiện với môi trường…Tại Hội thảo Địa nhiệt khu vực châu Á - Thái Bình Dương do Viện Khoa học Địa chất và Khoáng sản (Bộ Tài nguyên và Môi trường) phối hợp với Chương trình hợp tác công nghệ quốc tế của Cơ quan năng lượng quốc tế (IEA) tổ chức mới đây tại Hà Nội, đại diện lãnh đạo Bộ Tài nguyên và Môi trường cho biết: Chính phủ Việt Nam đã đề ra chủ trương phát triển kinh tế phải gắn với bảo vệ môi trường, xây dựng một nền kinh tế xanh. Phát triển kinh tế xanh đang là xu hướng lựa chọn cho một tương lai không thảm họa, thân thiện với môi trường sinh thái và ổn định lượng khí thải ra ở mức thấp… Không những thế, kinh tế xanh còn giúp các nước đang phát triển đạt được các lợi ích kinh tế và xã hội về nhiều mặt như phát triển năng lượng sạch, bền vững, đảm bảo an ninh năng lượng cho quốc gia và các ảnh hưởng môi trường được hạn chế.
[4] Theo thống kê, lĩnh vực sản xuất năng lượng chiếm đến 30% khí thải gây hiệu ứng nhà kính trên toàn cầu. Ở Việt Nam, con số này còn lớn hơn do khoảng 50% nguồn điện đến từ các nhà máy điện than và khí đốt. Bên cạnh đó, năng lượng tái tạo ở Việt Nam chỉ chiếm 6,28% trong các nguồn năng lượng và chủ yếu tới từ thủy điện nhỏ (chiếm đến 80%), còn địa nhiệt là 0%. Năm 2016, Việt Nam đã điều chỉnh sơ đồ quy hoạch phát triển điện lực quốc gia giai đoạn 2011 – 2020 có xét đến 2030, theo đó, công suất các nhà máy điện năng lượng tái tạo phải đạt đến 9,9% vào năm 2020; 12,5% vào năm 2025 và 21% vào năm 2030. Tuy nhiên, địa nhiệt chưa được nhắc đến là một trong các nguồn năng lượng tái tạo đưa vào quy hoạch.
[5] Về tiềm năng địa nhiệt của Việt Nam, các chuyên gia, các nhà khoa học nhận định: Nghiên cứu địa nhiệt ở Việt Nam đã được quan tâm từ khá lâu, bắt đầu từ nghiên cứu các nguồn nước khoáng nóng trong các chương trình địa chất thủy văn với sự hợp tác với các chuyên gia đến từ Pháp, Mỹ, New Zealand, Italia… và gần đây là sự hỗ trợ của Nhật Bản trong nghiên cứu và lắp đặt hệ thống bơm địa nhiệt tầng nông. Qua các khảo sát nghiên cứu đánh giá, Việt Nam có tiềm năng địa nhiệt đáng kể và có thể phát triển các nhà máy điện địa nhiệt.
(Linh Đan, stnmt.kontum.gov.vn)
Trả lời cho các câu 41, 42, 43, 44, 45, 46, 47, 48, 49, 50 dưới đây:
Mục đích chính của bài viết này là gì?
Đáp án đúng là: A
Đọc, suy luận
Đáp án cần chọn là: A
Theo đoạn [1], nhận định nào sau đây KHÔNG ĐÚNG khi nhắc đến địa nhiệt:
Đáp án đúng là: B
Tìm từ khóa chính, đối chiếu với ngữ liệu
Đáp án cần chọn là: B
Ở Việt Nam việc nghiên cứu và phát triển công nghệ khai thác nguồn năng lượng địa nhiệt ngày càng phát triển nhanh về quy mô và hiệu suất
Đúng hay sai?
Đáp án đúng là: B
Tìm từ khóa chính, đối chiếu với ngữ liệu
Đáp án cần chọn là: B
Kéo thả các cụm từ phù hợp vào mỗi chỗ trống:
Việc sử dụng địa nhiệt đã dần trở nên trên thế giới. Tuy nhiên địa nhiệt vẫn chưa nằm trong được đưa vào quy hoạch ở Việt Nam dù cho việc nghiên cứu địa nhiệt được từ khá lâu
Đáp án đúng là: phổ biến; năng lượng tái tạo; quan tâm
Tìm từ khóa chính, đối chiếu với ngữ liệu
Đáp án cần chọn là: phổ biến; năng lượng tái tạo; quan tâm
Theo đoạn [4], ý nào dưới đây nhận định đúng về vấn đề liên quan đến năng lượng tái tạo ở nước ta?
(Chọn hai đáp án đúng)
Đáp án đúng là: C; D
Tìm từ khóa chính, đối chiếu với ngữ liệu
Đáp án cần chọn là: C; D
Điền một cụm từ không quá BỐN tiếng trong đoạn [5] vào chỗ trống:
__________________ ở Việt Nam bắt đầu từ nghiên cứu các nguồn nước khoáng nóng
Đáp án đúng là: nghiên cứu địa nhiệt
Tìm từ khóa chính, đối chiếu với ngữ liệu
Đáp án cần điền là: nghiên cứu địa nhiệt
Theo đoạn trích, Việt Nam có thể phát triển các nhà máy địa nhiệt
Đáp án đúng là: A
Tìm từ khóa chính, đối chiếu với ngữ liệu
Đáp án cần chọn là: A
Điền một cụm từ không quả BA tiếng trong bài đọc vào chỗ trống:
_______________ giúp các nước đang phát triển đạt được các lợi ích kinh tế và xã hội về nhiều mặt.
Đáp án đúng là: kinh tế xanh
Tìm từ khóa chính, đối chiếu với ngữ liệu, suy luận
Đáp án cần điền là: kinh tế xanh
Đọc đoạn [3] và [4] của bài, chọn hai đáp án đúng cho câu hỏi sau:
Tại sao địa nhiệt được cho là có tiềm năng phát triển tại Việt Nam?
Chọn hai đáp án đúng.
Đáp án đúng là: A; D
Tìm từ khóa chính, đối chiếu với ngữ liệu
Đáp án cần chọn là: A; D
Kéo thả các cụm từ phù hợp vào mỗi chỗ trống:
Khai thác địa nhiệt ở Việt Nam mở ra khai thác, ứng dụng vào sẽ giải quyết hai bài toán và
Đáp án đúng là: triển vọng; thực tế; đồng thời; kinh tế; môi trường
Tìm từ khóa chính, đối chiếu với ngữ liệu
Đáp án cần chọn là: triển vọng; thực tế; đồng thời; kinh tế; môi trường
Đọc văn bản dưới đây và trả lời câu hỏi:
Xử lý rác thải y tế bằng phương pháp hấp nhiệt ướt
[1] Nhu cầu từ thực tiễn
Chất thải y tế là loại chất thải rất nguy hại, có độc tính cao, khả năng lây nhiễm mạnh, nếu không được xử lý khoa học sẽ gây ảnh hưởng nghiêm trọng tới môi trường và sức khỏe cộng đồng. Theo thống kê của Tổ chức Y tế thế giới (WHO), khoảng 80% chất thải từ các cơ sở y tế là chất thải thông thường, 20% còn lại là chất thải nguy hại. Hiện nay trên thế giới (và cả ở Việt Nam) đang áp dụng 2 công nghệ chính để xử lý rác thải y tế lây nhiễm, đó là công nghệ đốt và không đốt. Ở các nước phát triển, công nghệ không đốt đã được thay thế hoàn toàn cho công nghệ đốt.
Tại Việt Nam, hầu hết các cơ sở y tế đang sử dụng lò đốt để xử lý rác thải y tế nguy hại. Công nghệ đốt giúp loại bỏ hoàn toàn các chất lây nhiễm có trong rác thải y tế thành khí CO2 và hơi nước ở nhiệt độ khoảng 1.000oC. Tuy nhiên, công nghệ này có nhược điểm là khi đốt sẽ gây ra chất thải thứ phát là dioxin và furan - những độc tố ảnh hưởng nghiêm trọng tới sức khỏe con người và môi trường.
Hiện nay với sự tiến bộ của khoa học và công nghệ, nhiều phương pháp xử lý chất thải đã ra đời, giúp xử lý triệt để các chất/ hợp chất nguy hại có trong rác thải y tế mà vẫn đảm bảo tiêu chuẩn về môi trường, trong đó phải kể đến công nghệ nghiền hấp tiệt trùng. Nguyên lý hoạt động của công nghệ này là dùng hơi nước bão hòa ở nhiệt độ cao để khử toàn bộ vi trùng, vi khuẩn và những tác nhân gây bệnh có hại. Mặc dù đã có một số đơn vị ứng dụng công nghệ này vào lĩnh vực xử lý chất thải y tế, tuy nhiên đây là công nghệ - thiết bị nhập khẩu nên doanh nghiệp gặp nhiều khó khăn khi tiến hành bảo trì, bảo dưỡng, hay thay thế nếu gặp sự cố.
[2] Một công trình mang nhiều ý nghĩa
Để từng bước chuyển đổi công nghệ xử lý rác thải y tế truyền thống, đáp ứng nhu cầu của xã hội, Viện Nghiên cứu Cơ khí đã đề xuất và được phê duyệt thực hiện đề tài: “Nghiên cứu, thiết kế, chế tạo và đưa vào vận hành hệ thống xử lý rác thải y tế bằng phương pháp hấp nhiệt ướt, năng suất 4.000-4.500 kg rác/ngày”. Sau 2 năm triển khai thực hiện (2019-2020), các nhà khoa học của Viện đã chế tạo thành công 1 nồi hấp, 1 nồi hơi, 1 tủ điều khiển nồi hấp, 1 tủ điều khiển nồi hơi (phần cứng, phần mềm điều khiển) và bộ quy trình công nghệ xử lý rác thải y tế hấp nhiệt ướt. Sản phẩm đã được Bộ Tài nguyên và Môi trường cấp phép vận hành thử nghiệm (Công văn số 6524/ BTNMT-TCM ngày 18/11/2020). Điểm đặc biệt của thiết bị do Viện thiết kế, chế tạo là toàn bộ quá trình xử lý rác được vận hành tự động, khi hết thời gian khử trùng, rác được làm nguội và nghiền nhỏ, ép thành bánh, sau đó có thể tiến hành chôn lấp như chất thải thông thường.
Sau hai tháng được lắp đặt thử nghiệm tại Công ty Cổ phần vật tư thiết bị môi trường 13 (URENCO 13) cho thấy, hệ thống vận hành ổn định; các xét nghiệm vi sinh rác thải y tế sau khi được xử lý đạt kết quả theo yêu cầu của Viện Vệ sinh dịch tễ Trung ương.
[3] Đặc biệt, hệ thống xử lý rác thải y tế do Viện Nghiên cứu Cơ khí chế tạo còn có ưu điểm hơn hẳn, như thời gian xử lý rác rút ngắn xuống chỉ còn khoảng 80-85%, năng suất tăng khoảng 15-20%, giá thành chỉ bằng 1/3 so với giá nhập ngoại. Có thể khẳng định, việc các nhà khoa học trong nước nghiên cứu, chế tạo thành công hệ thống xử lý rác thải y tế bằng phương pháp hấp nhiệt ướt đã mang lại nhiều ý nghĩa quan trọng, cụ thể như:
Thứ nhất, về khả năng ứng dụng: hiện tại dây chuyền xử lý rác thải bằng công nghệ hấp nhiệt ướt đang được vận hành tại URENCO 13 đã chứng minh được tính ưu việt và mang lại hiệu quả kinh tế cao. Trước mắt, hệ thống sẽ được nhân rộng tại các đơn vị thành viên của URENCO phục vụ xử lý rác thải y tế tập trung cho các bệnh viện tại khu vực Hà Nội và một số tỉnh phía Bắc, sau đó sẽ nhân rộng sang các đơn vị xử lý rác thải bệnh viên tại miền Trung và miền Nam
Thứ hai, về hiệu quả môi trường và xã hội: công nghệ xử lý rác thải y tế bằng hấp nhiệt ướt không phát sinh chất thải thứ phát là dioxin và furan như công nghệ đốt. Với công nghệ này, Việt Nam sẽ thực hiện tốt hơn các công ước về bảo vệ môi trường đã ký kết với quốc tế như: Công ước về bảo vệ tầng ôzôn 1985, Tuyên bố của Liên hợp quốc về môi trường và phát triển 1992, Công ước khung của Liên hợp quốc về biến đổi khí hậu (UNFCCC) 1992, Công ước Stockholm về các chất ô nhiễm hữu cơ khó phân hủy (POP) 2001..., tạo ra môi trường trong sạch cho xã hội.
Thứ ba, về hiệu quả kinh tế: theo báo cáo của Công ty URENCO 13, chi phí xử lý rác thải y tế bằng công nghệ hấp nhiệt ướt đã giảm khoảng 40% so với công nghệ đốt, đồng thời chi phí bảo dưỡng, sửa chữa thấp hơn rất nhiều so với công nghệ và thiết bị nhập khẩu.
Ngoài ra, việc nghiên cứu, thiết kế, chế tạo dây chuyền xử lý rác thải y tế theo công nghệ mới đã khẳng định năng lực của các nhà khoa học trong nước trong việc làm chủ công nghệ thiết kế chế tạo thiết bị xử lý rác thải y tế, góp phần nâng cao sức khỏe người lao động và bảo vệ môi trường.
(Nguồn: Nguyễn Văn Bình, Đỗ Đình Hưởng; Tạp chí Khoa học và Công nghệ)
Trả lời cho các câu 51, 52, 53, 54, 55, 56, 57, 58, 59, 60 dưới đây:
Ý chính của văn bản trên là gì?
Đáp án đúng là: A
Tìm từ khóa chính, đối chiếu với ngữ liệu
Đáp án cần chọn là: A
Theo đoạn [1], nhận định nào sau đây KHÔNG ĐÚNG khi nhắc đến việc xử lý chất thải y tế hiện nay.
Đáp án đúng là: A
Tìm từ khóa chính, đối chiếu với ngữ liệu
Đáp án cần chọn là: A
Ở các nước đang phát triển công nghệ không đốt đã được thay thế hoàn toàn cho công nghệ đốt
Đúng hay sai?
Đáp án đúng là: B
Tìm từ khóa chính, đối chiếu với ngữ liệu
Đáp án cần chọn là: B
Kéo thả các cụm từ phù hợp vào mỗi chỗ trống:
Chất thải y tếchiếm phần lớn các chất thải y tế số còn lại là chất thải. Nếu không được xử lýsẽ gây ảnh hưởng đến sức khỏe con người và môi trường.
Đáp án đúng là: thông thường; nguy hại; khoa học
Tìm từ khóa chính, đối chiếu với ngữ liệu
Đáp án cần chọn là: thông thường; nguy hại; khoa học
Theo đoạn [1], tác giả đã đưa ra những lí giải nào để chứng minh rằng hệ thống xử lí rác thải y tế bằng phương pháp hấp nhiệt ướt ưu việt hơn công nghệ đốt và không đốt?
(Chọn hai đáp án đúng)
Đáp án đúng là: A; C
Tìm từ khóa chính, đối chiếu với ngữ liệu
Đáp án cần chọn là: A; C
Điền một cụm từ không quá BỐN tiếng trong đoạn [3] vào chỗ trống:
POP được hiểu là các chất ô nhiễm ___________khó phân hủy
Đáp án đúng là: hữu cơ
Tìm từ khóa chính, đối chiếu với ngữ liệu
Đáp án cần điền là: hữu cơ
Theo đoạn trích, dioxin và furan là chất thải thứ phát của quá trình xử lý rác thải y tế nói chung
Đúng hay sai?
Đáp án đúng là: B
Tìm từ khóa chính, đối chiếu với ngữ liệu
Đáp án cần chọn là: B
Điền một cụm từ không quả BA tiếng trong bài đọc vào chỗ trống:
Việc xử lý rác thải y tế bằng công nghệ hấp nhiệt ướt ở Việt Nam có mang_____________môi trường tốt. Bởi không phát sinh chất thải thứ phát là dioxin và furan như công nghệ đốt.
Đáp án đúng là: hiệu quả
Tìm từ khóa chính, đối chiếu với ngữ liệu
Đáp án cần điền là: hiệu quả
Đọc đoạn [3] của bài, chọn hai đáp án đúng cho câu hỏi sau:
Hệ thống xử lý rác thải y tế do Viện Nghiên cứu Cơ khí chế tạo còn có ưu điểm hơn hẳn bởi lẽ:
Chọn hai đáp án đúng.
Đáp án đúng là: B; D
Tìm từ khóa chính, đối chiếu với ngữ liệu
Đáp án cần chọn là: B; D
Kéo thả các cụm từ phù hợp vào mỗi chỗ trống:
Quy trình xử lí rác thải bằng phương pháp hấp nhiệt ướt là, , , ,
Đáp án đúng là: khử trùng; làm nguội; nghiền nhỏ; ép thành bánh; chôn lấp
Tìm từ khóa chính, đối chiếu với ngữ liệu
Đáp án cần chọn là: khử trùng; làm nguội; nghiền nhỏ; ép thành bánh; chôn lấp
Phần 3: Tư duy khoa học/Giải quyết vấn đề
Đọc đoạn văn sau và trả lời các câu hỏi bên dưới:
Trong cuộc sống hằng ngày, chúng ta gặp rất nhiều các chuyển động đu đưa, vật chuyển động luôn thay đồi chiều, đi qua đi lại quanh một vị trí cân bằng, chuyển động đó gọi đó là dao động. Dao động mà phương trình có dạng \(x = A\cos (\omega t + \varphi )\) gọi là dao động điều hòa, trong đó x là li độ, A là biên độ của dao động, \(\omega \) là tần số góc của dao động và \(\varphi \) là pha ban đầu.
Sau đây, chúng ta sẽ xét một hệ dao động đơn giản nhất là dao động của con lắc đơn. Con lắc đơn được cấu tạo bởi một dây mảnh có chiều dài l. Một đầu của dây được nối với một vật nặng có khối lượng m và một đầu được treo cố định trên giá tại điểm O. Kéo vật nặng ra khỏi vị trí cân bằng một góc \(\alpha \) rồi buông tay. Dưới tác dụng của trọng lực, vật nặng sẽ dao động. Quỹ đạo chuyển động của vật nặng được mô tả trên hình. Chu kì dao động T (hoặc tần số dao động f) của vật quanh vị trí cân bằng C được xác định bởi: \(T = \dfrac{1}{f} = \dfrac{{2\pi }}{\omega } = 2\pi \sqrt {\dfrac{l}{g}} \), trong đó, g là gia tốc trọng trường của Trái Đất tại vị trí đặt hệ con lắc đơn (lấy \(g = 9,8\,\,m/{s^2}\)).
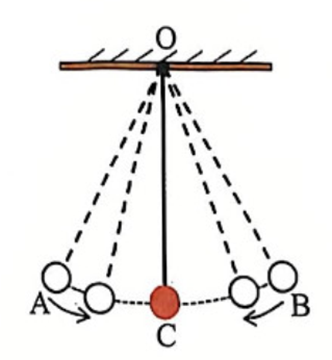
Chú ý: Để đơn giản, giả thiết dây không giãn, khối lượng không đáng kể và coi chuyển động của vật như chuyển động của chất điểm. Bỏ qua ma sát và lực cản của không khí trong quá trình vật chuyển động trong nội dung bài đọc cũng như trong câu hỏi.
Trả lời cho các câu 61, 62, 63, 64, 65, 66 dưới đây:
Đồ thị nào sau đây mô tả mối quan hệ giữa chu kỳ T và chiều dài l của con lắc đơn?
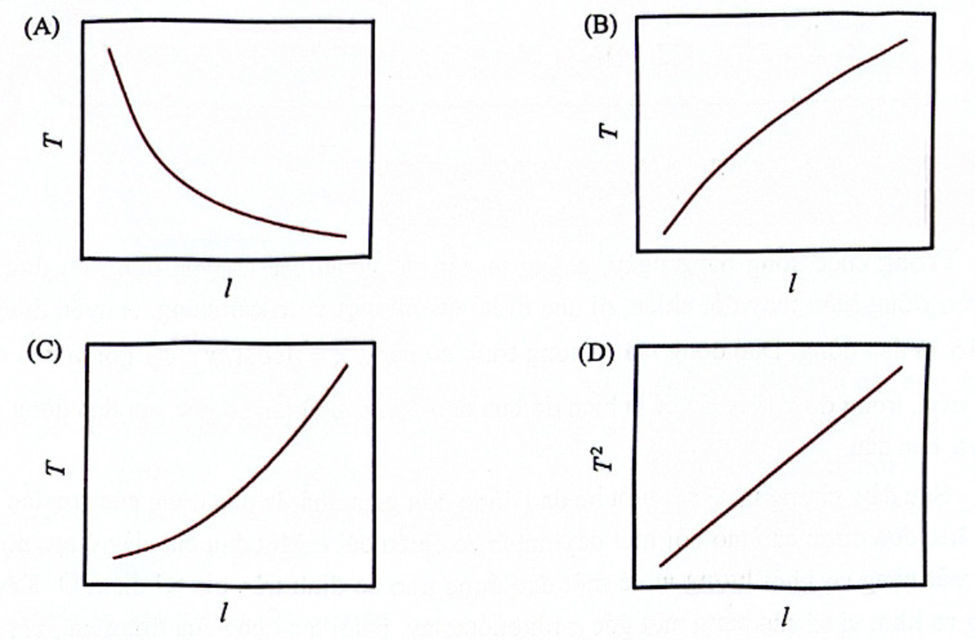
Đáp án đúng là: D
Sử dụng lý thuyết đồ thị của hàm số
Đáp án cần chọn là: D
Kéo vật nặng ra khỏi vị trí cân bằng các góc \(\alpha \) nhỏ, nhưng tăng dần theo thứ tự \({\alpha _l} < {\alpha _2} < {\alpha _3} < {\alpha _4}\), thể hiện tương ứng trên hình minh họa, rồi thả nhẹ. Nhận định nào sau đây về mối liên hệ giữa chu kỳ dao động T của con lắc theo góc lệch \(\alpha \) ban đầu?
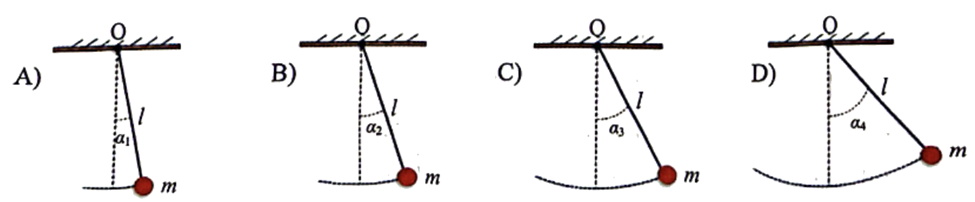
| Đúng | Sai | |
|---|---|---|
| a) Chu kỳ T tăng dần theo độ lớn góc lệch \(\alpha \) ban đầu. | ||
| b) Chu kỳ T nhỏ nhất ứng với trường hợp góc lệch \({\alpha _1}\). | ||
| c) Chu kỳ T lớn nhất ứng với trường hợp góc lệch \({\alpha _4}\). | ||
| d) Chu kỳ T không phụ thuộc vào góc lệch \(\alpha \) ban đầu. |
Đáp án đúng là: S; S; S; Đ
Sử dụng lý thuyết con lắc đơn
Đáp án cần chọn là: S; S; S; Đ
Hình A, B, C và D mô tả thí nghiệm xác định chu kỳ dao động T của con lắc đơn khi chiều dài l của con lắc đơn được giữ không đổi nhưng khối lượng vật nặng tăng từ m lên 4m, 9m và 16m. Kéo vật nặng ra khỏi vị trí cân bằng với cùng một góc \(\alpha \) nhỏ rồi buông không vận tốc ban đầu. Chu kỳ T của con lắc đơn sẽ:
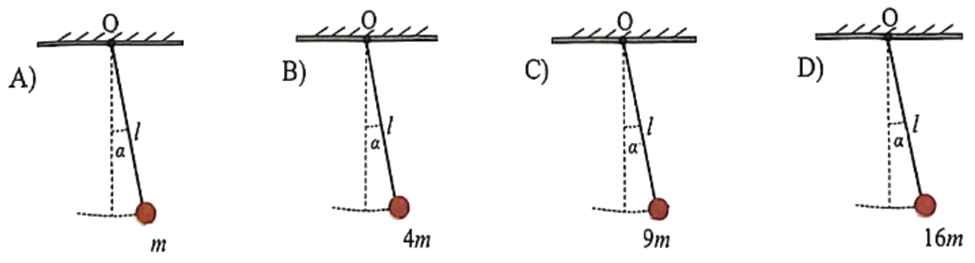
Đáp án đúng là: D
Sử dụng lý thuyết con lắc đơn
Đáp án cần chọn là: D
Trường hợp con lắc được làm bằng dây kim loại mảnh, chiều dài phụ thuộc vào nhiệt độ theo công thức \(l = {l_0}\left[ {1 + {\alpha _l}\left( {t - {t_0}} \right)} \right]\), trong đó, l và \({l_0}\) lần lượt là chiều dài của con lắc ở nhiệt độ t và \({t_0},{\alpha _1}\) là hệ số giãn nở nhiệt của vật liệu \(\left( {{\alpha _l} = {{17.10}^{ - 6}}{K^{ - 1}}} \right)\). Khi hệ con lắc dao động ở nhiệt độ phòng \({t_0} = {23^0}C\) thì tần số dao động của vật là \({f_0}\). Khi nhiệt độ trong phòng tăng lên \({t_1} = {32^0}C\) thì tần số dao động của vật là \({f_1}\). Tần số \({f_1} > {f_0}\) là đúng hay sai?
Đáp án đúng là: B
Chu kì con lắc đơn: \(T = 2\pi \sqrt {\dfrac{l}{g}} \)
Đáp án cần chọn là: B
Để đo gia tốc trọng trường của Trái Đất, một học sinh thiết kế hệ dao động của con lắc đơn. Hệ con lắc đơn bao gồm vật nặng khối lượng m = 16,6 g, treo trên một dây không giãn có chiều dài l = 500 mm. Sau đó kéo vật nặng ra khỏi vị trí cân bằng một góc nhỏ rồi buông nhẹ tay. Đồ thị sự phụ thuộc góc lệch \(\alpha \) theo thời gian t được vẽ trên đồ thị máy tính thể hiện trên hình. Dùng chức năng công cụ để xác định vị trí đồ thị cắt trục hoành theo thời gian tại các vị trí như trên hình (các chấm đen).
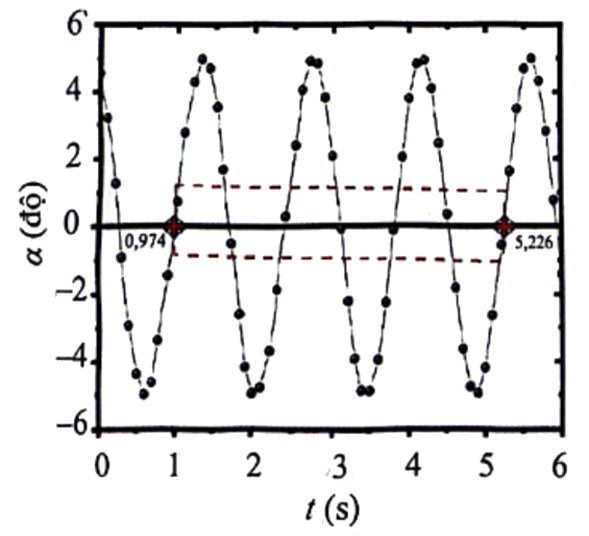
Dựa trên số liệu thu được, chu kỳ dao động T của con lắc đơn bằng (s) và giá trị gia tốc trọng trường g tại nơi làm thí nghiệm bằng \(\left( {m/{s^2}} \right)\).
Chú ý: Lấy giá trị \(\pi = 3,14\).
Đáp án đúng là: 1,417; 9,82
Sử dụng kĩ năng đọc đồ thị
Chu kì của con lắc đơn: \(T = 2\pi \sqrt {\dfrac{l}{g}} \)
Đáp án cần chọn là: 1,417; 9,82
Một con lắc đơn có chiều dài dây treo 50 cm và vật nhỏ có khối lượng 0,01 kg mang điện tích \(q = + {5.10^{ - 6}}\,\,C\) được coi là điện tích điểm. Con lắc dao động điều hoà trong điện trường đều mà vectơ cường độ điện trường có độ lớn \(E = {10^4}\,\,V/m\) và hướng thẳng đứng xuống dưới. Lấy \(\pi = 3,14\). Chu kì dao động điều hoà của con lắc là
Đáp án đúng là: C
Lực điện: \(\overrightarrow F = q\overrightarrow E \)
Gia tốc do lực điện gây ra: \(\overrightarrow a = \dfrac{{\overrightarrow F }}{m}\)
Gia tốc trọng trường hiệu dụng: \(\overrightarrow {{g_{HD}}} = \overrightarrow g + \overrightarrow a \)
Chu kì dao động của con lắc đơn: \(T = 2\pi \sqrt {\dfrac{l}{{{g_{HD}}}}} \)
Đáp án cần chọn là: C
Đọc đoạn văn sau và trả lời các câu hỏi bên dưới:
Sự rơi tự do được định nghĩa là sự rơi của các vật dưới tác dụng của trọng lực. Nếu vật rơi trong không khí mà độ lớn của lực cản không khí không đáng kể so với trọng lượng của vật thì cũng gọi là rơi tự do.
Chuyển động rơi tự do là một chuyển động nhanh dần đều, theo phương thẳng đứng, chiều từ trên xuống. Ở cùng một nơi trên Trái Đất, các vật rơi tự do với cùng một gia tốc \(a = g = 9,8\,\,m/{s^2}\) (g gọi là gia tốc trọng trường).
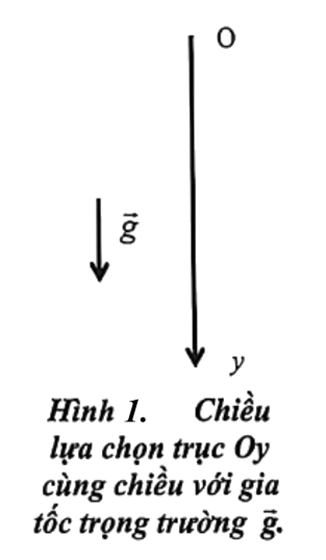
Để giải các bài toán về rơi tự do, thường chọn trục tọa độ Oy như hình, gốc tọa độ O tại vị trí bắt đầu rơi (ứng với vật ở độ cao h so với mặt đất), chiều dương Oy hướng từ trên xuống và gốc thời gian (t = 0) là lúc vật bắt đầu rởi. Khi đó, bài toán về rơi tự do như bài toán về chuyển động thẳng biến đổi đều với vận tốc ban đầu \({v_0} = 0\) và gia tốc a = g. Khi đó:
Tốc độ của vật sau khoảng thời gian t xác định bởi: v = gt. (1)
Quãng đường vật đi được sau khoảng thời gian t xác định bởi: \(s = \dfrac{1}{2}g{t^2}\). (2)
Ở đây, có mối liên hệ giữa tốc độ, gia tốc và quãng đường như sau: \({v^2} = 2gs\). (3)
Trả lời cho các câu 67, 68, 69, 70, 71, 72, 73 dưới đây:
Các mệnh đề nào sau đây không đúng?
Đáp án đúng là: C
Sử dụng thông tin từ văn bản
Đáp án cần chọn là: C
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
| Đúng | Sai | |
|---|---|---|
| a) Chuyển động của người nhảy dù là rơi tự do. | ||
| b) Vật rơi tự do là vật rơi chỉ dưới tác dụng của trọng lực. | ||
| c) Một vật rơi tự do không vận tốc ban đầu từ độ cao 5 m xuống. Tốc độ của nó sau 0,5 giây là 4,9 m/s. | ||
| d) Các mảnh giấy vụn li ti rơi xuống sau khi được bắn ra từ ống pháo giấy là rơi tự do. |
Đáp án đúng là: S; Đ; Đ; S
Sử dụng lý thuyết sự rơi tự do
Đáp án cần chọn là: S; Đ; Đ; S
Một quả bóng tennis bị rơi xuống từ mép sân thượng của một tòa nhà cao tầng, tới đất sau khoảng thời gian 5 s. Độ cao của toà nhà khi đó là:
Đáp án đúng là: B
Độ cao thả rơi vật: \(h = \dfrac{1}{2}g{t^2}\)
Đáp án cần chọn là: B
Kéo thả kết quả thích hợp vào chỗ trống:
Một vật được thả rơi tự do từ độ cao 80 m. Tốc độ rơi của vật sau 2 giây là: (m/s). Thời gian rơi của vật cho đến khi chạm đất là (s).
Đáp án đúng là: 19,6; 4
Tốc độ của vật sau khoảng thời gian t xác định bởi: v = gt. (1)
Quãng đường vật đi được sau khoảng thời gian t xác định bởi: \(s = \dfrac{1}{2}g{t^2}\). (2)
Đáp án cần chọn là: 19,6; 4
Điền kết quả thích hợp vào chỗ trống:
Thả một hòn đá rơi (coi là rơi tự do) từ miệng một cái hang sâu xuống đến đáy. Sau 4 s kể từ lúc bắt đầu thả thì nghe tiếng hòn đá chạm vào đáy. Biết tốc độ truyền âm trong không khí là 330 m/s. Chiều sâu của hang là _____ (m). (Làm tròn kết quả đến một chữ số sau dấu phẩy).
Đáp án đúng là: 70,3
Thời gian vật rơi tự do: \(h = \dfrac{1}{2}g{t^2}\)
Công thức tính thời gian vật chuyển động thẳng đều: \(t = \dfrac{s}{v}\)
Đáp án cần điền là: 70,3
Trong 1s cuối cùng trước khi chạm đất, một vật rơi tự do đi được quãng đường gấp 2 lần quãng đường vật rơi trước đó tính từ lúc thả. Tốc độ của vật ngay khi sắp chạm đất là:
Đáp án đúng là: B
Tốc độ của vật trước khi chạm đất: \(v = \sqrt {2gh} \)
Quãng đường vật rơi tự do trong t giây đầu: \(s = \dfrac{1}{2}g{t^2}\)
Đáp án cần chọn là: B
Từ một đỉnh tháp người ta thả rơi tự do vật thứ nhất. Hai giây sau, ở tầng tháp thấp hơn 39,2 m, người ta thả rơi tự do vật thứ hai. Sau bao lâu hai vật sẽ chạm nhau tính từ lúc vật thứ nhất được thả rơi?
Đáp án đúng là: C
Phương trình tọa độ - thời gian: \(y = {y_0} + \dfrac{1}{2}g.{\left( {t - {t_0}} \right)^2}\)
Hai vật gặp nhau: \({y_1} = {y_2}\)
Đáp án cần chọn là: C
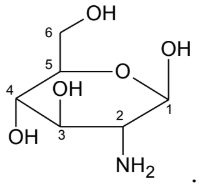
Glucosamine có vai trò quan trọng trong việc phát triển và duy trì gân, dây chằng, sụn và chất lỏng bao quanh khớp, giúp ngăn ngừa sự thoái hoá khớp. Glucosamine là hợp chất thu được khi thay thế nhóm -OH ở nguyên tử carbon số 2 trong glucose bằng nhóm -NH2. Khi cho glucosamine phản ứng với hydrochloric acid thu được glucosamine hydrochloride có dạng R-NH3Cl (chất được sử dụng làm thực phẩm chức năng, hỗ trợ quá trình điều chế bệnh đau xương khớp).
Glucosamine và glucosamine hydrochloride có thể được điều chế từ chitin. Chitin được tìm thấy trong vỏ của động vật giáp xác, xương động vật.
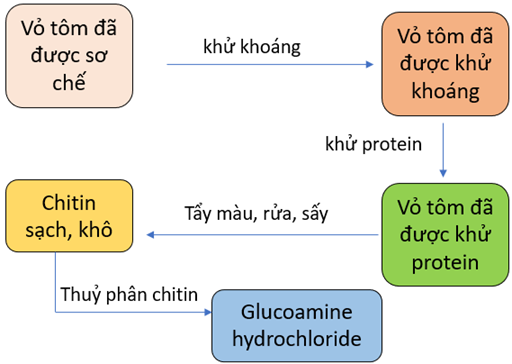
Hình 1: Quy trình điều chế glucosamine từ vỏ tôm
Có 3 nhóm học sinh trong một lớp tiến hành thí nghiệm điều chế chitin từ 35 gam vỏ tôm đã được làm sạch. Kết quả thí nghiệm của các nhóm được cho trong bảng 1:

Sau đó, các nhóm tiếp tục điều chế glucosamine hydrochloride từ chitin sạch, kết quả thu được của các nhóm được cho trong bảng 2:

Trả lời cho các câu 74, 75, 76, 77, 78, 79, 80 dưới đây:
Kéo thả từ/cụm từ thích hợp vào chỗ trống?
Glucosamine hydrochloride được điều chế bằng cách cho glucosamine tác dụng với dung dịch. Ngoài ra, glucosamine hydrochloride còn được điều chế từ (thành phần có nhiều trong ).
Đáp án đúng là: HCl; chitin; vỏ tôm
Phân tích dữ liệu đoạn văn.
Đáp án cần chọn là: HCl; chitin; vỏ tôm
Công thức cấu tạo của glucosamine là
Đáp án đúng là: B
Glucosamine là hợp chất thu được khi thay thế nhóm -OH ở nguyên tử carbon số 2 trong glucose bằng nhóm -NH2.
Đáp án cần chọn là: B
Quy trình điều chế glucosamine hydrochloride trải qua
Đáp án đúng là: D
Từ quy trình điều chế glucosamine.
Đáp án cần chọn là: D
Khoáng chất trong vỏ tôm gồm calcium carbonate, magnesium carbonate và calcium phosphate. Để khử khoáng, các học sinh đã dùng dung dịch HCl 10% để khử. Trong quá trình khử khoáng, hiện tượng quan sát được là
Đáp án đúng là: A
Tính chất hoá học của acid, muối.
Đáp án cần chọn là: A
Điền số thích hợp vào chỗ trống?
Phần trăm khối lượng protein trung bình có trong vỏ tôm là_____%.
(làm tròn kết quả đến hàng phần mười)
Đáp án đúng là: 24,8
Trong quá trình điều chế chitin, phải trải qua giai đoạn khử khoáng sau đó là khử protein. Do đó, khối lượng vỏ tôm chênh lệch giữa hai giai đoạn là khối lượng protein có trong vỏ tôm.
⟹ Phần trăm khối lượng protein trung bình có ở vỏ tôm
Đáp án cần điền là: 24,8
Phát biểu sau là đúng hay sai?
| Đúng | Sai | |
|---|---|---|
| a) Glucosamine phản ứng với HCl theo tỉ lệ 1 : 1 | ||
| b) Glucosamine hydrochloride có nhiều trong động vật giáp xác, xương động vật. | ||
| c) Khối lượng khoáng trung bình trong vỏ tôm là khoảng 15,8 gam. | ||
| d) Nhóm 3 có hiệu suất điều chế glucosamine hydrochloride cao nhất. |
Đáp án đúng là: Đ; S; Đ; S
Phân tích dữ liệu đề bài, suy luận.
Đáp án cần chọn là: Đ; S; Đ; S
Trong giai đoạn từ chitin để tạo thành glucosamine hydrochloride, nhóm học sinh thực hiện theo 2 bước như sau:
Bước 1: Thuỷ phân chitin trong dung NaOH.
Bước 2: Sản phẩm thu được ở bước 1 là chitosan và đem thuỷ phân trong dung dịch HCl.
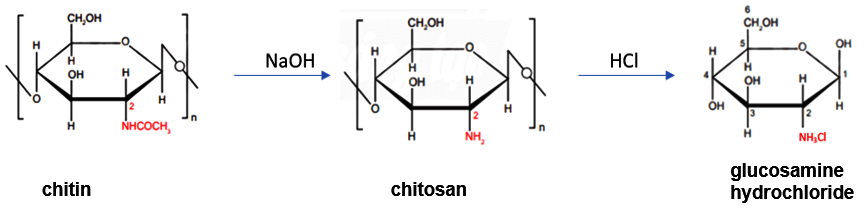
Mục địch chính của của giai đoạn 1 là
Đáp án đúng là: A
Từ CTCT của chitin, xác định liên kết tham gia phản ứng hoá học.
Đáp án cần chọn là: A
Để sản xuất glucose bằng phương pháp sinh học, bột khoai lang được hòa với nước (chỉnh pH của dịch về 4,2), hàm lượng bột khoai là 20% khối lượng. Chế phẩm thương mại Stargen 002 (chứa hệ enzyme amylase phân giải tinh bột thành đường) được bổ sung với hàm lượng 1,5 mL/kg bột khoai, rồi tiến hành phản ứng thủy phân ở các nhiệt độ khác nhau là 30, 40, 50 và 55 °C. Hiệu suất của quá trình thủy phân được xác định bằng tỷ lệ giữa lượng glucose thu được sau phản ứng chia cho lượng glucose lý thuyết (quy đổi từ tinh bột trong bột khoai ban đầu). Ảnh hưởng của nhiệt độ phản ứng đến hiệu suất thủy phân được trình bày trong bảng 1.
Bảng 1. Ảnh hưởng của nhiệt độ đến hiệu suất thủy phân bột khoai lang

(Nguồn: Ảnh hưởng của nhiệt độ và nồng độ chất khô đến quá trình thủy phân bột khoa lang không hồ hóa, Tạp chí Nông nghiệp và Phát triển nông thôn 2019, số 372, trang 63 – 69)
Trả lời cho các câu 81, 82, 83 dưới đây:
Phát biểu dưới đây là đúng hay sai?
| Đúng | Sai | |
|---|---|---|
| a) Glucose được tạo thành bằng cách phân giải tinh bột có trong bột khoai. | ||
| b) Tác nhân chính để phân giải tinh bột trong bột khoai là H+ từ môi trường pH thấp (pH = 4,2). | ||
| c) Trong nghiên cứu trên, glucose được điều chế bằng phương pháp hoá học. | ||
| d) Phản ứng thuỷ phân tinh bột trên được thực hiện trong môi trường acid. |
Đáp án đúng là: Đ; S; S; Đ
Phân tích dữ liệu đoạn văn để suy luận các phát biểu.
Đáp án cần chọn là: Đ; S; S; Đ
Kéo thả từ/cụm từ thích hợp vào chỗ trống?
Mối liên hệ giữa nhiệt phản ứng và hiệu suất thuỷ phân làvới nhau.
Đáp án đúng là: tỉ lệ thuận
Từ bảng số liệu và suy ra nhận định.
Đáp án cần chọn là: tỉ lệ thuận
Biết bột khoai lang chứa 68% khối lượng là tinh bột, hệ số chuyển đổi tinh bột sang glucose là 10/9. Tính % theo khối lượng glucose thu được sau khi kết thúc thủy phân ở 55 °C?
Đáp án đúng là: B
Tính toán lượng tinh bột có trong bột khoai ứng với nồng độ ban đầu là 20%, sau đó quy đổi sang lượng glucose lý thuyết và nhân với hiệu suất thủy phân.
Đáp án cần chọn là: B
Nước chlorine có tính sát khuẩn. Vì vậy, dung dịch này được và dụng khi trùng nước sinh hoạt tại các nhà máy xử lý và cấp nước. Trong quá trình khử trùng người ta phải cho một lượng chlorine (Cl2) dư vào nước sinh hoạt. Lượng chlonine dư có tác dụng ngăn ngừa nước bị tái nhiễm vi khuẩn trong quá trình vận chuyển và lưu trữ.
Lượng chlorine dư trong nước có thể được xác định theo phương pháp chuẩn độ như sau (Tiêu chuẩn ngành 64TCN 115:1999): lấy 200 mL mẫu nước chứa chlorine tác dụng với Kl dư để giải phóng ra l2. Thêm vào bình phản ứng 10 mL dung dịch Na2S2O3 0,02 M. Phần Na2S2O3 không phản ứng sẽ được chuẩn độ bằng dung dịch I2 0,05 M với chất chỉ thị hồ tinh bột, khi hai chất phản ứng vừa đủ với nhau thì ghi lại thể tích dung dịch là tiêu tốn là V mL.
Các phản ứng hóa học xảy ra trong quá trình này là:
Cl₂ + 2KI → 2KCI + I2 (1)
I2 + 2Na2S2O3 → 2NaI + Na2S4O6 (2)
Trả lời cho các câu 84, 85, 86, 87 dưới đây:
Phát biểu nào sau đây sai?
Đáp án đúng là: B
Phân tích đoạn ngữ liệu kết hợp lí thuyết về phản ứng oxi hoá – khử.
Đáp án cần chọn là: B
Phản ứng (1) chứng tỏ
Đáp án đúng là: A; C
Lí thuyết về phản ứng oxi hoá - khử
Đáp án cần chọn là: A; C
Kéo thả từ/cụm từ thích hợp vào chỗ trống?
Dung dịch nước chlorine có môi trường
Đáp án đúng là: acid
Tính chất hoá học của chlorine.
Đáp án cần chọn là: acid
Giả sử V = 1,9 mL. Nguyên tử khối của Cl là 35,5. Hàm lượng chlorine dư mẫu nước là______ mg L-1 (kết quả làm tròn đến hàng phần nghìn).
Đáp án đúng là: 1,775
Tính Na2S2O3 ban đầu, dựa vào số mol của chuẩn độ với I2 ⟹ Mol Na2S2O3 phản ứng với I2 của phương trình (1) ⟹ Số mol Cl2
Đáp án cần điền là: 1,775
Đọc đoạn văn sau và trả lời 6 câu hỏi tiếp theo
Một nhà khoa học đã thử nghiệm khả năng tiêu diệt vi khuẩn kháng penicillin của 5 loại thuốc.
Thí nghiệm 1
Số lượng vi khuẩn kháng penicillin bằng nhau được đưa vào các bình chứa $10,0 \mathrm{ml}$ môi trường dinh dưỡng. Các bình được ủ trong 1 giờ ở 37 độ C cùng với các nồng độ khác nhau của 5 loại thuốc được trình bày trong Bảng 1 . Bình đối chứng bao gồm các vi khuẩn được ủ trong môi trường không có bất kỳ loại thuốc nào. Sau đó, vi khuẩn được rửa sạch để loại bỏ vết thuốc còn sót lại và nuôi cấy trên đĩa thạch dinh dưỡng trong 7 ngày. Trong thời gian này, vi khuẩn sinh sản, tạo thành các khuẩn lạc, sau đó được đếm vào cuối ngày thứ bảy. Các đĩa có nhiều khuẩn lạc hơn được cho là có nhiều vi khuẩn sống hơn vào cuối thời gian ủ 1 giờ. Bảng 1 cho thấy số lượng khuẩn lạc được đếm. Kiểm soát không có thuốc cho thấy 50 khuẩn lạc vào cuối 7 ngày.
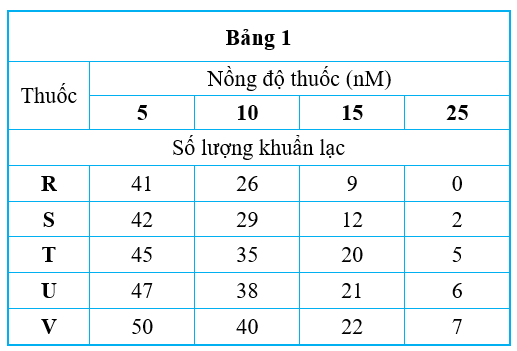
Thí nghiệm 2
Vi khuẩn được xử lý như mô tả trong thí nghiệm 1 nhưng ở thí nghiệm 2 tất cả các loại thuốc được dùng ở cùng một nồng độ và thời gian ủ của mỗi lần nuôi cấy là khác nhau. Bảng 2 cho thấy số lượng khuẩn lạc được đếm cho thí nghiệm 2.
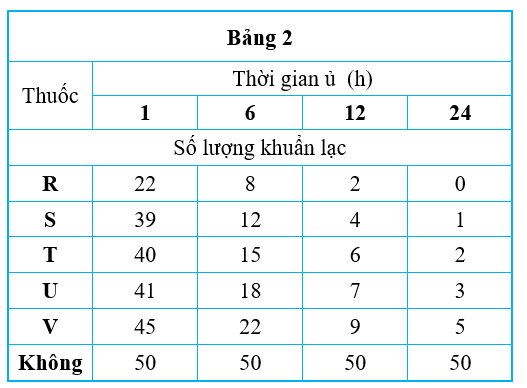
Thí nghiệm 3
Các hệ số thấm đo khả năng của thuốc xuyên qua màng tế bào của vi khuẩn. Hệ số thấm càng lớn thì khả năng vận chuyển thuốc qua màng càng nhanh. Khối lượng phân tử, tính bằng đơn vị khối lượng nguyên tử (amu) và hệ số thấm tính bằng centimet trên giây (cm/s) của 5 loại thuốc ở 37 độ C đã được đo. Các kết quả được thể hiện trong Bảng 3.
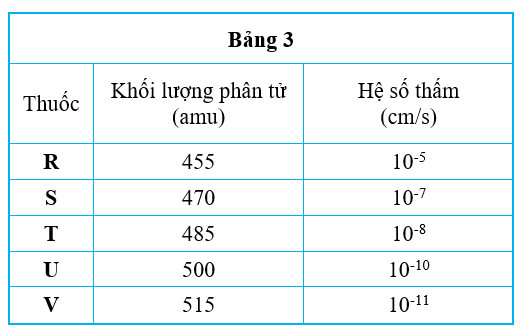
Trả lời cho các câu 88, 89, 90, 91, 92, 93 dưới đây:
Điền từ thích hợp vào chỗ trống
Theo thí nghiệm 1, ở nồng độ _____________ nM, các loại thuốc trong nghiên cứu diệt khuẩn tốt nhất.
Đáp án đúng là: 25
Dựa vào thí nghiệm 1
Đáp án cần điền là: 25
Điền từ thích hợp vào chỗ trống
Theo thí nghiệm 1 , ở nồng độ 10 nM , thuốc ____________ diệt khuẩn hiệu quả nhất.
Đáp án đúng là: R
Dựa vào thí nghiệm 1.
Đáp án cần điền là: R
Nhận định dưới đây đúng hay sai?
Theo kết quả thí nghiệm 3 , thuốc R xâm nhập vào tế bào vi khuẩn nhanh nhất
Đáp án đúng là: A
Dựa vào thí nghiệm 3.
Đáp án cần chọn là: A
Nếu Thí nghiệm 2 được lặp lại với Thuốc $U$ và thời gian ủ là 3 giờ, số lượng khuẩn lạc đếm được rất có thể là:
Đáp án đúng là: C
Dựa vào thí nghiệm 2
Đáp án cần chọn là: C
Phát biểu nào sau đây mô tả đúng nhất mối quan hệ giữa khối lượng phân tử và hệ số thấm của thuốc, trong Thí nghiệm 3 ?
Đáp án đúng là: A
Dựa vào thí nghiệm 3
Đáp án cần chọn là: A
Phát biểu nào sau đây mô tả đúng nhất mối quan hệ giữa thời gian ủ và số lượng vi khuẩn sống trong Thí nghiệm 2?
Đáp án đúng là: B
Dựa vào thí nghiệm 2.
Đáp án cần chọn là: B
Dựa vào dữ liệu dưới đây, thí sinh trả lời 5 câu hỏi tiếp theo.
Ở người, gene ABO (gồm 3 allele IA, IB và IO, nằm trên nhiễm sắc thể số 9) và gene H (gồm 2 allele H và h, nằm trên nhiễm sắc thể số 19) cùng quy định nhóm máu. Sự hoạt động của các allele này được thể hiện theo sơ đồ sau:

Cho biết: Allele h là các dạng đột biến lặn hoàn toàn và không có khả năng hình thành kháng nguyên H trên bề mặt hồng cầu; người có kiểu gene hh sẽ có kiểu hình nhóm máu O dạng hiếm (kiểu hình Bombay). Theo M. E. Reid (2004), trong các cộng đồng người Đông Nam Á đang cân bằng di truyền về gene này, tỉ lệ kiểu hình Bombay rất hiếm gặp, chỉ được tìm thấy ở 1 trên 10 000 người.
Trong huyết tương ở người có 3 loại kháng thể là α, β và anti-H có khả năng gây ngưng kết và làm ly giải các hồng cầu có kháng nguyên lần lượt tương ứng là A, B và H, từ đó gây ra những phản ứng truyền máu nghiêm trọng có thể dẫn đến tử vong. Vì vậy trong lĩnh vực truyền máu huyết học, một nguyên tắc quan trọng cần phải tuân thủ là các tế bào hồng cầu của nguồn máu truyền vào không bị ngưng kết bởi các kháng thể có trong huyết tương của người nhận. Bình thường, trong huyết tương ở người có đầy đủ các loại kháng thể khác nhau, ngoại trừ loại kháng thể gây ngưng kết cho chính hồng cầu của cơ thể.
Trả lời cho các câu 94, 95, 96, 97, 98 dưới đây:
Trong các cộng đồng người đang cân bằng di truyền về cả 2 gene trên, nhóm máu nào sau đây được quy định bởi nhiều loại kiểu gene khác nhau nhất?
Đáp án đúng là: D
Dựa vào dữ liệu đề bài.
Đáp án cần chọn là: D
Trong phòng sanh của một bệnh viện tuyến tỉnh, có đầy đủ các túi máu thuộc các nhóm máu khác nhau và được bảo quản trong các ngăn khác nhau của tủ lạnh ở nhiệt độ 4oC với các nhãn ghi đầy đủ như sau:

Một sản phụ đang thực hiện thủ thuật sinh mổ, mất khá nhiều máu và cần phải truyền máu. Phát biểu nào sau đây đúng?
Đáp án đúng là: B
Dựa vào dữ liệu đề bài và sơ đồ truyền máu.
Đáp án cần chọn là: B
Phát biểu nào sau đây đúng khi nói về sự di truyền tính trạng nhóm máu ABO ở người?
Đáp án đúng là: B
Dựa vào dữ liệu đề bài.
Đáp án cần chọn là: B
Sinh viên T là sinh viên Trường Đại học Sư phạm Thành phố Hồ Chí Minh, thường tham gia vào các hoạt động hiến máu tình nguyện. Sinh viên này được xác định có nhóm máu B. Cho biết trường hợp nào sau đây có thể là kiểu gene của sinh viên T và nhóm máu của những người có thể nhận máu từ nguồn máu hiến tặng này?
Đáp án đúng là: C
Dựa vào dữ liệu đề bài.
Đáp án cần chọn là: C
M. A. Khan (2014) và các nghiên cứu khác đã công bố rằng tần số các allele IA, IB, IO và tỉ lệ các kiểu gene về locus này trong các cộng đồng người Kinh ở Việt Nam tuân theo định luật Hardy – Weinberg, các khác biệt không có ý nghĩa thống kê. Tỉ lệ % từng nhóm máu được trình bày ở bảng sau:
![]()
Trong một cộng đồng người Kinh ở Việt Nam đang cân bằng về hai gene ABO và H, một người phụ nữ có nhóm máu AB kết hôn với người chồng có kiểu hình Bombay. Biết rằng không xảy ra các đột biến mới, xác suất họ sinh được 1 người con có nhóm máu O là bao nhiêu?
Đáp án đúng là: B
Bài toán này yêu cầu tính xác suất sinh con có nhóm máu O từ một cặp vợ chồng có nhóm máu AB và Bombay. Ta cần phân tích đặc điểm di truyền của hai gene ABO và H để xác định kiểu gen của bố mẹ và khả năng tạo ra con có kiểu hình nhóm máu O.
Đáp án cần chọn là: B
Sơ đồ bên mô tả quá trình hình thành loài lúa mì ngày nay. Nghiên cứu sơ đồ và cho biết tính Đúng/Sai của các nhận định sau?
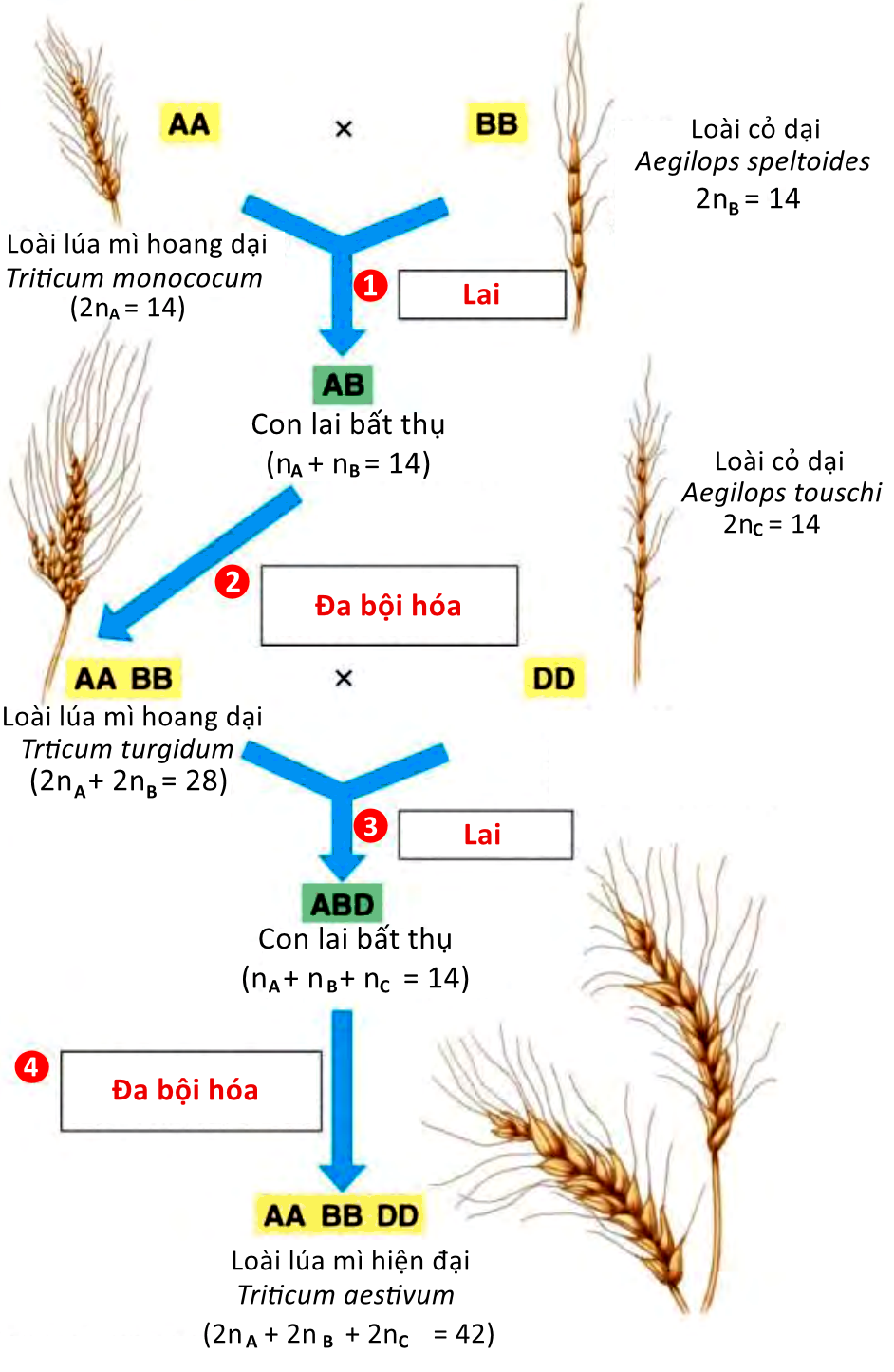
| Đúng | Sai | |
|---|---|---|
| a) Cây lai 1 và cây lai 2 đều bất thụ (không có khả năng sinh sản hữu tính). | ||
| b) Quá trình hình thành loài lúa mì ngày nay do 2 lần lai xa và 1 lần đa bội hóa. | ||
| c) Cây lai 1 và cây lai 2 có kí hiệu bộ NST lần lượt là nA + nB = 14 và nA + nB + nD = 21. | ||
| d) Lúa mì ngày nay có khả năng sinh sản hữu tính và có kiểu gen đồng hợp tất cả các cặp gene. |
Đáp án đúng là: S; S; S; Đ
Đọc và phân tích hình ảnh
Đáp án cần chọn là: S; S; S; Đ
Cho biết loài A là sinh vật sản xuất, trong các lưới thức ăn sau đây, lưới thức ăn ở hình nào dễ bị ảnh hưởng nhất khi loài B bị diệt vong?
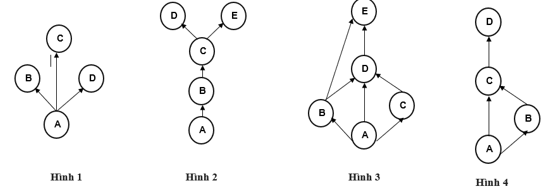
Đáp án đúng là: C
Vận dụng kiến thức đã học về hệ sinh thái.
Đáp án cần chọn là: C