Phần 1: Toán học và xử lý số liệu
Cho hàm số \(y = a{x^2} - bx + c\) có đồ thị như hình vẽ dưới đây:
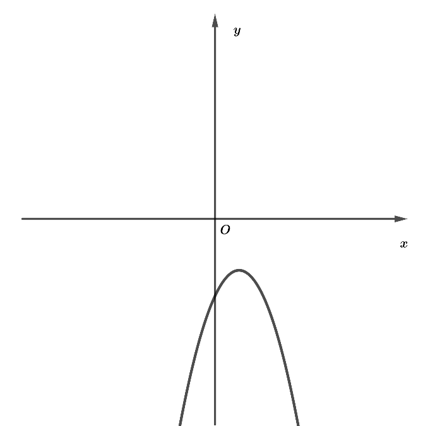
Trong các khẳng định sau, khẳng định nào đúng?
Đáp án đúng là: B
Xác định dấu dựa trên các đặc điểm của đồ thị hàm số.
Đáp án cần chọn là: B
Trong hệ toạ độ Oxy, cho đường tròn \((C)\) có phương trình \({\left( {x - 3} \right)^2} + {\left( {y - 4} \right)^2} = 25\) và điểm \(M\left( { - 4;3} \right)\). Gọi \(d:4x + ay + b = 0\)là một tiếp tuyến đi qua điểm \(M\)của đường tròn \(\left( C \right)\). Biết \(a < 0\), giá trị của biểu thức \(T = ab\) bằng:
Đáp án đúng là: B
Lập phương trình từ dữ kiện liên quan đến tiếp tuyến của đường tròn và đi qua một điểm.
Đáp án cần chọn là: B
Gieo ngẫu nhiên đồng thời ba con xúc xắc đồng chất. Xác suất để tích số chấm của mặt trên ba con xúc sắc bằng 36 gần nhất với giá trị nào sau đây:
Đáp án đúng là: C
Sử dụng phương pháp tính theo định nghĩa xác suất cổ điển.
Đáp án cần chọn là: C
Xét hình bình hành \(ABCD\) có tâm \(O\), đẳng thức nào sau đây là đúng?
Đáp án đúng là: B
Sử dụng những tính chất liên quan đến các vectơ bằng nhau.
Đáp án cần chọn là: B
Trong hệ toạ độ Descartes, gọi \(\left( D \right)\)là miền đa giác được tạo bởi các bất phương trình sau: \(\left\{ \begin{array}{l}2x + 3y \le 10\\x - 2y \le 4\\x \ge 0\\2x - y \ge 1\end{array} \right.\)
Trong các điểm dưới đây, điểm nào không nằm trong miền đa giác \(\left( D \right)\)?
Đáp án đúng là: D
Kiểm tra các điểm đã cho có thoả mãn tất cả các bất đẳng thức đã cho hay không.
Đáp án cần chọn là: D
Có bao nhiêu số nguyên dương \(m\)nhỏ hơn 100 thoả mãn phương trình
\(\dfrac{1}{{{{\log }_m}3}}.\cos 3x + {\log _9}m.\sin 3x = \sqrt {{{\log }_3}\dfrac{m}{{81}}} \)
có nghiệm? (nhập đáp án vào ô trống)
Đáp án đúng là: 19
Sử dụng điều kiện có nghiệm của phương trình \(a.\sin x + b.\cos x = c\)có nghiệm.
Đáp án cần điền là: 19
Cho dãy số \(\left\{ {{u_n}} \right\}\) được xác định bởi công thức truy hồi: \(\left\{ \begin{array}{l}{u_1} = 4\\{u_{n + 1}} = 3{u_n} - 6n + {2^n} + 3\,\left( {n \in {N^*}} \right)\end{array} \right.\)
Chữ số cuối cùng của \({u_{2024}}\) là bao nhiêu? (nhập đáp án vào ô trống)
Đáp án đúng là: 7
Từ công thức truy hồi tìm công thức tổng quát của dãy số.
Đáp án cần điền là: 7
Một cấp số cộng có số hạng đầu là \({u_1} = 2025,\)công sai \(d = - 5.\) Hỏi bắt đầu từ số hạng nào của cấp số cộng đó thì nó nhận giá trị âm
Đáp án đúng là: B
Đáp án cần chọn là: B
Cho dãy số \(\left( {{u_n}} \right)\)có giới hạn hữu hạn bằng \(a\) khi \(n\) dần tiến tới dương vô cực. Khẳng định nào sau đây là đúng?
Đáp án đúng là: A
Kết hợp định nghĩa khi \(\lim \,{u_n} = 0\)và khi \(\lim \,{u_n} = a\).
Đáp án cần chọn là: A
Xét hàm số \(f\left( x \right) = \sqrt {a{x^2} - 3} + \sqrt {b{x^2} + 12x + 3} - 5x\,\,\left( {a,\,b > 0} \right)\). Biết \(a + b = 13\), đồng thời \(f\left( x \right)\) có giới hạn hữu hạn khi \(x \to + \infty \). Khi đó, tính giá trị nhỏ nhất của\(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\). (nhập đáp án vào ô trống)
Đáp án đúng là: 2
Sử dụng phương pháp liên hợp
Đáp án cần điền là: 2
Cho hàm số \(y = \dfrac{{x + 1}}{{x - 3}}\) có đồ thị \(\left( C \right)\). Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ \({x_0} = 1 + \sqrt 2 + \sqrt 5 \) cùng với 2 tiệm cận của đồ thị hàm số tạo thành một tam giác. Diện tích của tam giác tạo thành bằng:
Đáp án đúng là: C
Giải bài toán tổng quát với hoành độ \({x_0} = a + 3\) bất kỳ.
Đáp án cần chọn là: C
Tìm tập xác định của hàm số \(y = \ln \left( {\ln \left( {2{x^2} - \dfrac{1}{x}} \right)} \right)\).
Đáp án đúng là: B
Tìm điều kiện để hàm số ln xác định.
Đáp án cần chọn là: B
Để tiết kiệm, một người quyết định trích ra một số tiền hàng tháng để gửi vào ngân hàng. Cứ đầu mỗi tháng, người đó gửi 2 000 000 đồng vào ngân hàng. Biết rằng lãi suất hàng tháng của ngân hàng là 0,8% (sẽ được tính vào giữa tháng), và số tiền lãi của tháng đó và số tiền gửi vào thêm sẽ được gộp vào số tiền gốc để tính lãi cho tháng sau. Hỏi sau 4 năm, tài khoản tiết kiệm của người đó có bao nhiêu tiền? (nhập đáp án vào ô trống, đơn vị: triệu đồng, kết quả là tròn đến hàng đơn vị)
Đáp án đúng là: 117
Tìm công thức tổng quát của số tiền
Đáp án cần điền là: 117
Carbon-14 (\(^{14}C\)) là một đồng vị phóng xạ của nguyên tố carbon. Trong môi trường tự nhiên, \(^{14}C\) luôn luôn phân rã thành các đồng vị không phóng xạ của nó. Số nguyên tử \(^{14}C\) sau một khoảng thời gian được tính bằng công thức sau:
\(N\left( t \right) = {N_0}.{e^{ - \lambda t}}\)
trong đó, \(N\left( t \right)\)là số nguyên tử \(^{14}C\) sau một thời gian \(t\), \({N_0}\) là số nguyên tử \(^{14}C\) tại thời điểm ban đầu, \(\lambda \) là một hằng số.
Biết rằng cứ sau 5730 năm, số lượng nguyên tử \(^{14}C\) sẽ mất đi một nửa. Hỏi cứ sau bao nhiêu năm, số lượng nguyên tử \(^{14}C\) sẽ giảm đi 5 lần? (nhập đáp án vào ô trống, kết quả làm tròn đến hàng đơn vị )
Đáp án đúng là: 13305
Sử dụng công thức đã cho để lập phương trình
Đáp án cần điền là: 13305
Trong không gian, cho các đường thẳng phân biệt \(a,\,b\) và các mặt phẳng phân biệt \(\left( P \right),\,\left( Q \right)\). Trong các mệnh đề sau, mệnh đề nào sai?
Đáp án đúng là: D
Nắm chắc lý thuyết về mối quan hệ vuông góc, song song trong không gian.
Đáp án cần chọn là: D
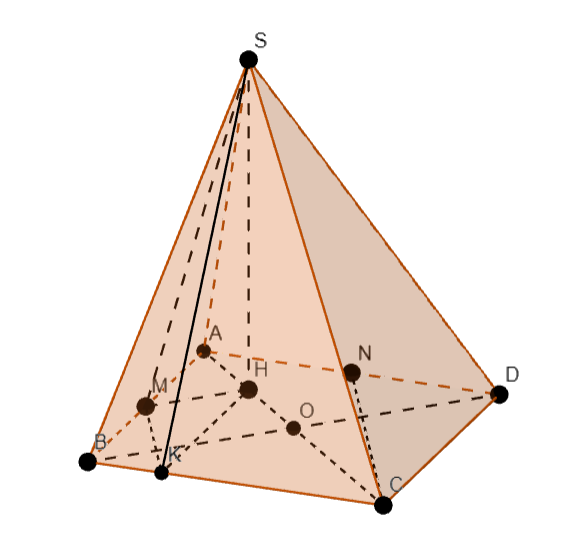
Cho hình chóp \(S.ABCD\) có đáy là hình vuông tâm \(O\) cạnh \(a\). Hình chiếu vuông góc của \(S\) xuống mặt phẳng đáy là trung điểm của \(AO\). Gọi \(M,\,N\) lần lượt là trung điểm của \(AB,\,AD\). Biết thể tích của hình chóp là \(V = \dfrac{{2{a^3}}}{3}\), góc giữa hai đường thẳng \(SM\) và \(CN\) gần nhất với giá trị nào sau đây?
Đáp án đúng là: A
Chọn đường thẳng trung gian song song với một đường thẳng và cắt đường thẳng còn lại.
Đáp án cần chọn là: A
Cho hình chóp \(S.ABCD\)có đáy là hình thoi tâm \(O\) cạnh \(a\), \(\widehat {BAD} = {135^0}\). Biết \(SA = 2a\) và tạo với mặt phẳng đáy một góc 600. Gọi \(I\) là trung điểm của \(SO\),\(\left( P \right)\)là mặt phẳng đi qua \(BI\) và song song với cạnh \(AC\), \(\left( P \right)\) chia hình chóp \(S.ABCD\)thành hai phần. Biết thể tích của phần nhỏ hơn là \(\dfrac{{{a^3}\sqrt m }}{n}\), với \(m,\,n \in {\mathbb{N}^*};\,m + n < 60\). Tính giá trị của biểu thức \(T = \dfrac{n}{{{m^2}}}\). (nhập đáp án vào ô trống)
Đáp án đúng là: 1
Tính các tỉ lệ độ dài, từ đó sử dụng tỉ số thể tích.
Đáp án cần điền là: 1
Sử dụng dữ liệu sau để trả lời các câu hỏi từ 18 đến 20:
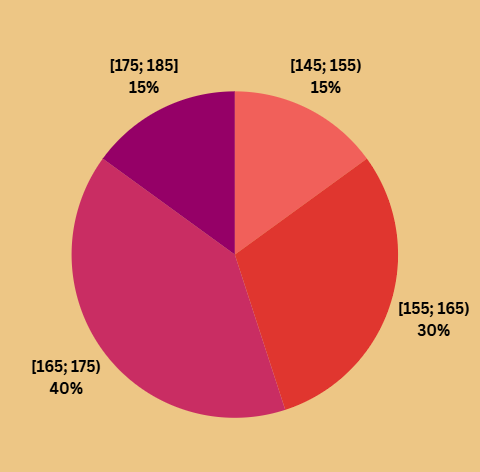
Trả lời cho các câu 18, 19, 20 dưới đây:
Trung bình chiều cao các học sinh trong lớp là:
Đáp án đúng là: C
Công thức tính giá trị trung bình
Đáp án cần chọn là: C
Trung vị chiều cao các học sinh trong lớp là bao nhiêu?
Đáp án đúng là: A
Sắp xếp mẫu số liệu theo thứ tự không giảm tìm nhóm chứa trung vị từ đó áp dụng công thức tìm trung vị
Đáp án cần chọn là: A
Phương sai chiều cao các học sinh trong lớp gần nhất với giá trị nào sau đây:
Đáp án đúng là: B
Áp dụng công thức tính trung bình mẫu, trung vị, phương sai cho mẫu số liệu ghép nhóm.
Đáp án cần chọn là: B
Một sinh viên mới ra trường nộp đơn ứng tuyển vào ba công ty khác nhau. Biết rằng xác suất để sinh viên đó trúng tuyển vào ba công ty lần lượt là 0,6; 0,7 và 0,5, đồng thời việc trúng tuyển hay không trúng tuyển vào một công ty không làm ảnh hưởng tới cơ hội trúng tuyển vào các công ty khác. Xác suất để nhân viên đó trúng tuyển đúng một công ty là bao nhiêu?
Đáp án đúng là: C
Sử dụng công thức cộng xác suất và công thức nhân xác suất đối với các biến cố độc lập.
Đáp án cần chọn là: C
Nam chơi một trò chơi như sau: Nam có hai chiếc hộp, chiếc hộp thứ nhất chứa \(x\) quả bóng màu đỏ, \(y\) quả bóng màu xanh, chiếc hộp thứ hai chứa \(z\) quả bóng màu đỏ, \(t\) quả bóng màu xanh \(\left( {x,\,y,\,z,\,t\, \in {\mathbb{N}^*}} \right)\). Nam lấy ngẫu nhiên một quả bóng từ hộp thứ nhất sang hộp thứ hai, sau đó lại lấy ngẫu nhiên hai quả bóng từ hộp thứ hai ra.
Gọi \(A\)là biến cố “Lấy được quả bóng màu xanh từ hộp thứ nhất”, \(B\)là biến cố “Lấy được hai quả bóng khác màu từ hộp thứ hai”. Với bộ giá trị nào của \(x,\,y,\,z,\,t\) sau đây thì \(A\) và \(B\)là hai biến cố độc lập?
Đáp án đúng là: C
Chỉ ra \(P\left( {AB} \right) = P\left( A \right)P\left( B \right)\).
Đáp án cần chọn là: C
Cho \(P\left( A \right) = 0,7;\,P\left( B \right) = 0,6;\,P\left( {A\overline B } \right) = 0,3\). Tính \(P\left( {B|\overline A } \right)\). (nhập đáp án vào ô trống, điền dưới dạng phân số tối giản, tử số và mẫu số ngăn cách nhau bởi dấu “/”)
Đáp án đúng là: 2/3
Áp dụng các công thức về xác suất có điều kiện, xác suất toàn phần.
Đáp án cần điền là: 2/3
Trong một căn phòng có 2025 bóng đèn, được đánh số theo thứ tự từ 1 đến 2025. Ban đầu, tất cả các đèn còn đang tắt. Cứ sau mỗi phút, các đèn lại thay đổi trạng thái với quy luật:
Tại phút thứ \(i\), các đèn được đánh số là bội số của \(i\) sẽ thay đổi trạng thái, các đèn còn lại giữ nguyên trạng thái.
(Lưu ý: Thay đổi trạng thái có nghĩa là từ trạng thái tắt chuyển sang trạng thái bật, và từ trạng thái bật chuyển sang trạng thái tắt).
Sau đúng 2025 phút, có \(k\) đèn trong căn phòng đó đang tắt. Khẳng định nào sau đây là không đúng?
Đáp án đúng là: A
Đáp án cần chọn là: A
Một con kiến di chuyển trên một bàn cờ từ ô vuông A đến ô vuông B như hình vẽ. Trong một lần di chuyển, con kiến chỉ có thể di chuyển sang ô bên phải hoặc xuống ô phía dưới. Trong bàn cờ có một số ô vuông chứa các vật cản được đánh dấu “×”, con kiến không thể đi vào các ô vuông đó. Hỏi con kiến có bao nhiêu cách đi từ ô vuông A tới ô vuông B?
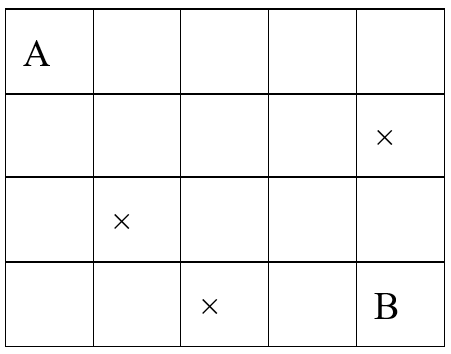
Đáp án đúng là: B
Tìm số cách đi đến từng ô vuông một.
Đáp án cần chọn là: B
Cho hàm số \(f\left( x \right) = \dfrac{{{x^2} - 3x - 4}}{{{x^2} - 4x + 3}}\). Hàm số đã cho đồng biến trên các khoảng nào trong các khoảng sau đây:
Đáp án đúng là: B
Tính đạo hàm của hàm số sau đó xét tính đơn điệu của hàm số.
Đáp án cần chọn là: B
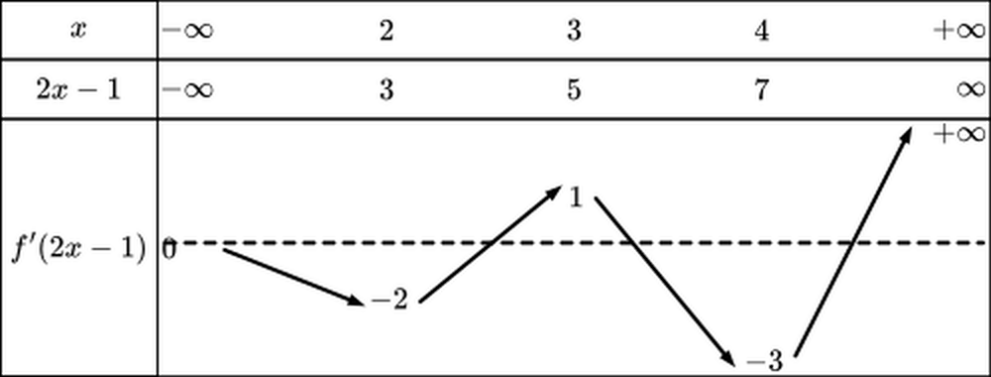
Xét hàm số \(f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\). Bảng biến thiên của hàm số \(y = f'\left( {2x - 1} \right)\) có dạng như dưới đây:
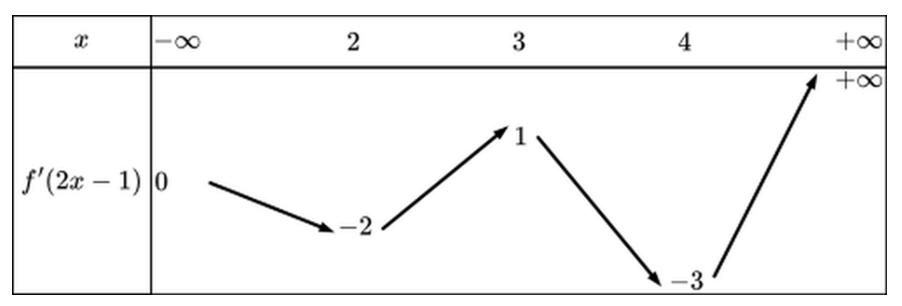
Hỏi hàm số \(g\left( x \right) = f\left( {{x^2} - 4x + 3} \right)\) đồng biến trên khoảng nào sau đây:
Đáp án đúng là: A
Từ bảng biến thiên suy ra nghiệm của phương trình \(f'\left( x \right) = 0\), từ đó suy ra tính đơn điệu của hàm số đề bài yêu cầu.
Đáp án cần chọn là: A
Xét hàm số \(y = {x^3} - {m^2}{x^2} + {m^3}x - {m^3}\). Hỏi có bao nhiêu giá trị nguyên của \(m\)để đồ thị hàm số của hàm số trên không có điểm cực trị nào?
Đáp án đúng là: B
Nếu hàm bậc ba không có điểm cực trị nào thì đạo hàm của hàm số đó luôn không dương hoặc không âm.
Đáp án cần chọn là: B
Cho hàm số \(y = f\left( x \right)\)có đạo hàm xác định trên \(\mathbb{R}\). Bảng biến thiên của \(f'\left( x \right)\) được cho như hình vẽ dưới đây.
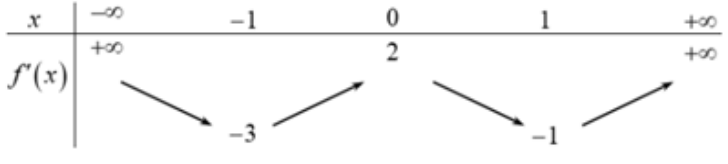
Số điểm cực trị của hàm số \(y = f\left( {{x^2} - 2x} \right)\)là:
Đáp án đúng là: C
Tính đạo hàm của hàm số.
Đáp án cần chọn là: C
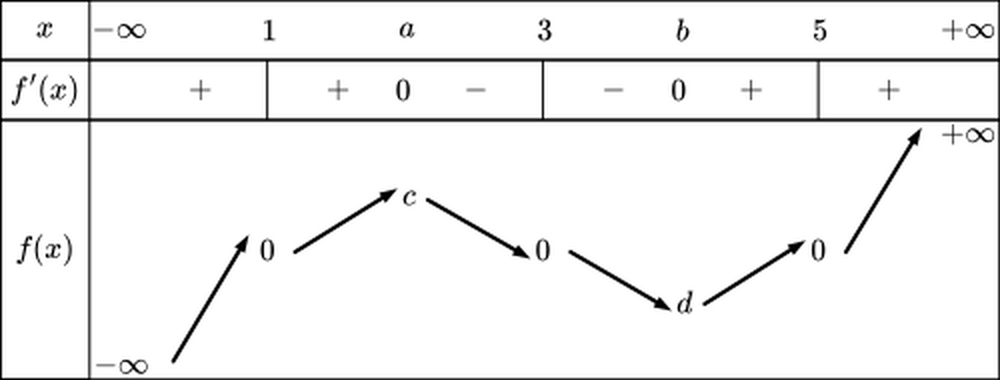
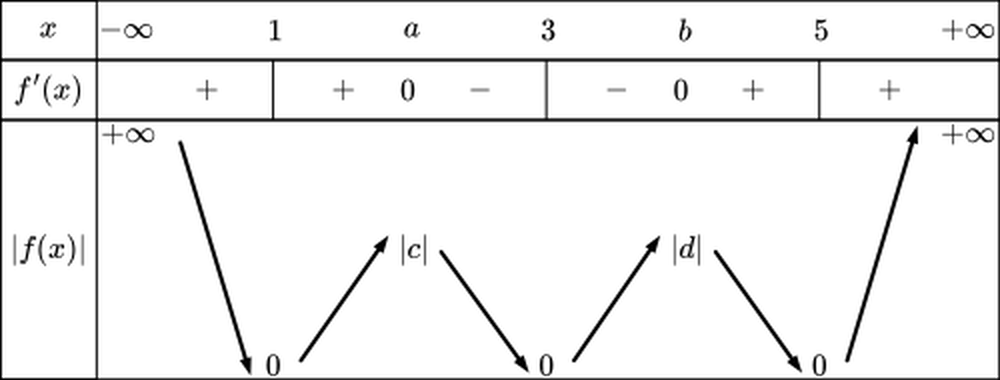
Đồ thị hàm số \(y = \left| {\left( {x - 1} \right)\left( {x - 3} \right)\left( {x - 5} \right)} \right|\)có bao nhiêu điểm cực tiểu? (nhập đáp án vào ô trống)
Đáp án đúng là: 3
Vẽ bảng biến thiên của hàm số.
Đáp án cần điền là: 3
Có bao nhiêu giá trị nguyên của tham số \(m \in \left[ { - 100;100} \right]\) để hàm số \(y = \left( {{x^9} + 8{x^7} + 6{x^5} + m{x^3}} \right)\left( {{x^8} + 7{x^4}} \right) + 3m\) nhận \({x_0} = 0\) làm điểm cực tiểu?
Đáp án đúng là: C
Xét dấu của đạo hàm hàm số trên với các giá trị của \(m\).
Đáp án cần chọn là: C
Tổng của giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = 2{\left( {2\cos x - 3} \right)^3} + 3{\left( {2\cos x - 3} \right)^2} - 24\cos x\) trên đoạn \(\left[ { - \dfrac{\pi }{3};\dfrac{{2\pi }}{3}} \right]\) là:
Đáp án đúng là: A
Đặt ẩn phụ.
Đáp án cần chọn là: A
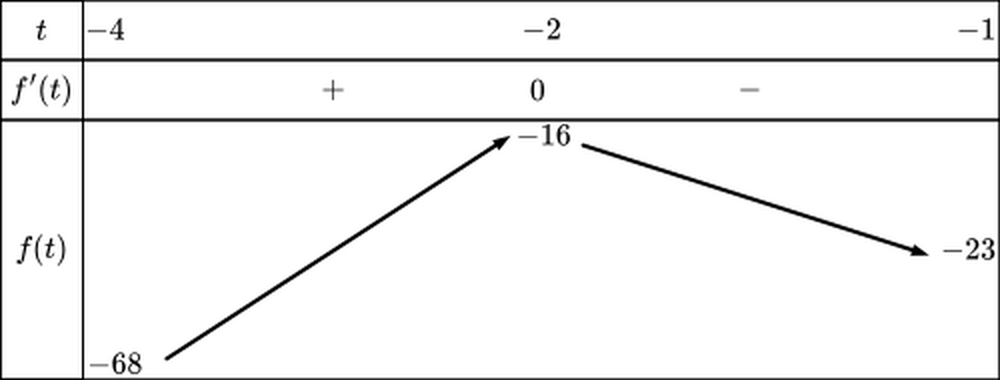
Tìm \(m\) để giá trị nhỏ nhất hàm số \(f\left( x \right) = {x^2} + \dfrac{m}{x} + m\) trên \(\left( {0; + \infty } \right)\) bằng 176. (nhập đáp án vào ô trống)
Đáp án đúng là: 128
Vẽ bảng biến thiên của hàm số cho từng trường hợp của \(m\).
Đáp án cần điền là: 128
Một nhà máy cần sản xuất một loại bao bì bằng bìa để đựng sản phẩm của mình. Đối với mỗi sản phẩm, nhà máy sẽ có thể sử dụng 250 cm2 bìa để làm bao bì. Có hai phương án sản xuất bao bì cho nhà máy như sau
- Phương án 1: Bao bì có dạng hình trụ.
- Phương án 2: Bao bì có dạng hình hộp chữ nhật, với đáy hộp có dạng hình vuông.
Lưu ý, các loại bao bì cần phải có đủ hai đáy.
Hỏi thể tích lớn nhất mà bao bì có thể tạo thành là bao nhiêu? (nhập đáp án vào ô trống, làm tròn kết quả đến hàng đơn vị, đơn vị cm3 )
Đáp án đúng là: 303
Xét hai trường hợp, đối với mỗi trường hợp lập hàm số, tìm thể tích lớn nhất có thể.
Đáp án cần điền là: 303
Tổng số tiệm cận (đứng, ngang, xiên) của đồ thị hàm số \(y = \dfrac{{{x^2} + \ln \left( {{x^2} - 2x} \right)}}{x}\) là:
Đáp án đúng là: C
Xét giới hạn hàm số đã cho tại các cận.
Đáp án cần chọn là: C
Biết tiệm cận xiên của đồ thị hàm số \(y = \dfrac{{{m^2}{x^2} - 2mx - n}}{{2x - 6}}\,\left( {m \ne 0} \right)\) luôn là tiếp tuyến của đồ thị hàm số \(y = \dfrac{{ - 1}}{{2x + k}}\)khi \(m,\,n\) thay đổi. Giá trị của \(k\) bằng bao nhiêu? (nhập đáp án vào ô trống)
Đáp án đúng là: 6
Tìm phương trình tiệm cận xiên của đồ thị hàm số
Đáp án cần điền là: 6
Cho một hàm số bậc bốn và một hàm số bậc nhất có đồ thị như hình vẽ sau:
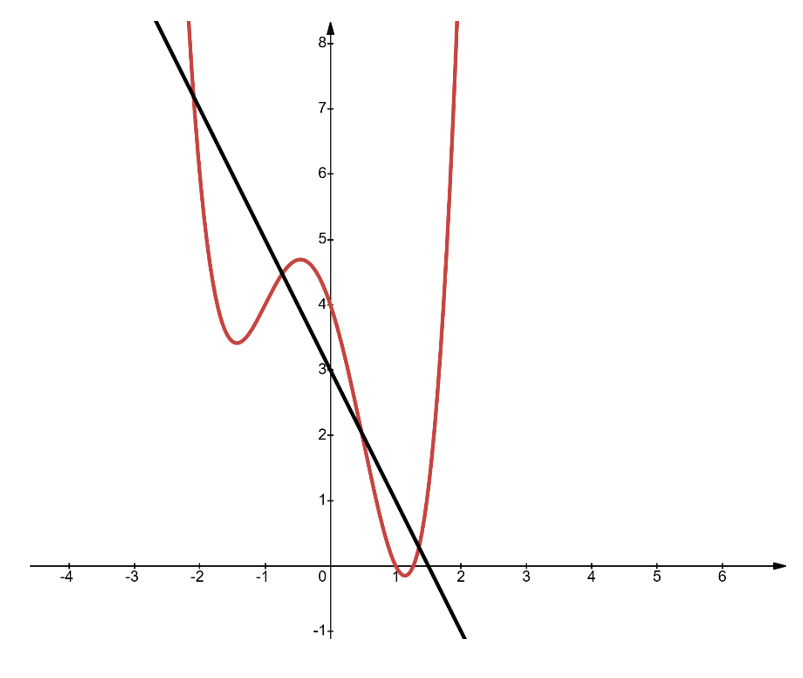
Tích các hoành độ giao điểm của hai đồ thị hàm số trên bằng bao nhiêu? Biết hệ số ứng với số hạng bậc cao nhất của hàm số bậc bốn là 1.
Đáp án đúng là: A
Vận dụng định lý Vi-ét.
Đáp án cần chọn là: A
Cho \(f\left( x \right),\,g\left( x \right)\) là các hàm số bậc 4 và bậc 3. Biết đồ thị các hàm số \(f'\left( x \right),\,g'\left( x \right)\) được cho bởi hình vẽ dưới đây. Hỏi hàm số \(h\left( x \right) = f\left( {{x^2} - 2x} \right) - g\left( {{x^2} - 2x} \right)\) có bao nhiêu điểm cực trị?
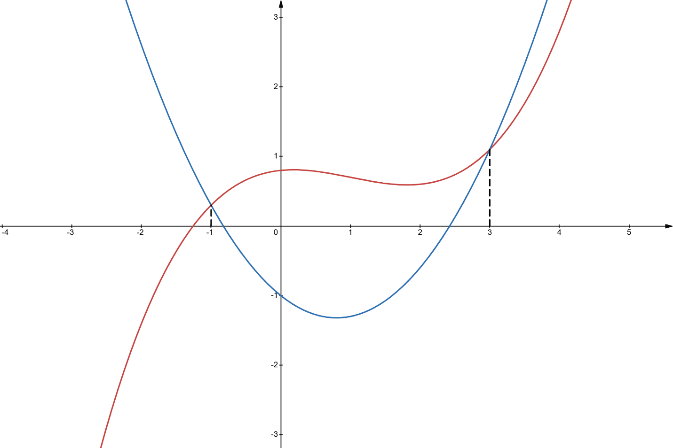
Đáp án đúng là: C
Xác định nghiệm của phương trình \(f'\left( x \right) - g'\left( x \right) = 0\), từ đó xác định nghiệm của phương trình \(h'\left( x \right) = 0\)
Đáp án cần chọn là: C
Trong không gian, cho đường thẳng \(d:\left\{ \begin{array}{l}x = t - 1\\y = 2t + 2\\z = 3t\end{array} \right.\) và điểm \(M\left( {4;\, - 8;\,5} \right)\). Đường thẳng đi qua điểm \(M\), cắt và vuông góc với đường thẳng \(d\)nhận vectơ nào sau đây là vectơ chỉ phương?
Đáp án đúng là: B
Tìm toạ độ giao điểm của hai đường thẳng.
Đáp án cần chọn là: B
Trong không gian Oxyz, cho các điểm \(A\left( {2;7;5} \right)\), \(B\left( {3;6;4} \right)\), \(C\left( {1;8;2} \right)\), \(D\left( {4;3;2} \right)\). Toạ độ điểm \(M\)sao cho biểu thức \(T = M{A^2} + M{B^2} - M{C^2} + 2M{D^2}\) đạt giá trị nhỏ nhất là \(\left( {a;b;c} \right)\). Giá trị biểu thức \(P = \dfrac{{ab}}{c}\) bằng bao nhiêu? (nhập đáp án vào ô trống)
Đáp án đúng là: 4
Lựa chọn điểm trung gian sau đó sử dụng phương pháp vectơ.
Đáp án cần điền là: 4
Trong không gian Oxyz, cho tứ diện đều\(ABCD\). Biết toạ độ của 2 điểm \(A,\,B\)là \(A\left( {1;1;1} \right)\), \(B\left( {1,3,1} \right)\), điểm \(C\) nằm trên mặt phẳng \(Oxy\) và có hoành độ dương, điểm \(D\) có cao độ dương. Biết toạ độ của điểm \(D\) là \(D\left( {1 + \sqrt a ,\,b,\,c} \right)\), với là các số nguyên.
Tính giá trị của biểu thức \(T = a + b + c\). (nhập đáp án vào ô trống)
Đáp án đúng là: 6
Sử dụng các điều kiện của tứ diện đều.
Đáp án cần điền là: 6
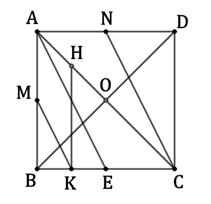
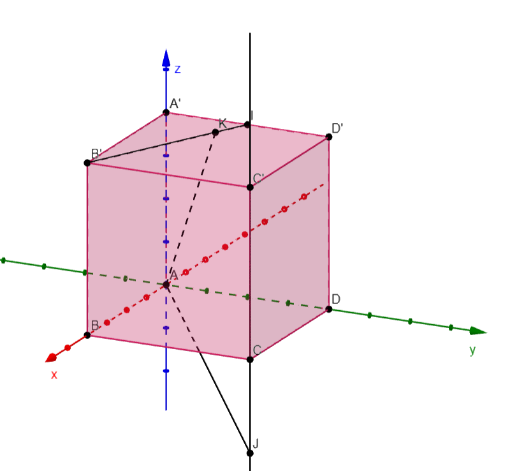
Trong không gian, cho hình lập phương \(ABCD.A'B'C'D'\). Gọi \(I\) là trung điểm của cạnh \(A'D'\), \(J\) là điểm nằm trên đường thẳng \(CC'\). Khi \(d\left( {AJ,\,B'I} \right)\) đạt giá trị lớn nhất, tỉ số \(\dfrac{{JC}}{{JC'}}\) bằng bao nhiêu?
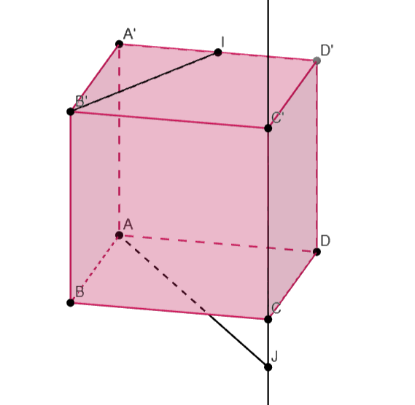
Đáp án đúng là: C
Toạ độ hoá hình đã cho.
Đáp án cần chọn là: C
Biết giá trị của tích phân \(I = \int\limits_{ - 2}^{ - 1} {\dfrac{{3x + 3}}{{{x^2} - 4x + 3}}dx} \) bằng. Biết \(I = a.\ln 2 + b.\ln 3 - c.\ln 5\), với \(a,b,c\)là các số tự nhiên. Giá trị của biểu thức \(T = a + b + c\)bằng:
Đáp án đúng là: C
Phân tích hàm cần tính tích phân thành các hàm sơ cấp có thể lấy tích phân.
Đáp án cần chọn là: C
Một chất điểm chuyển động có vận tốc được thể hiện ở đồ thị bên.
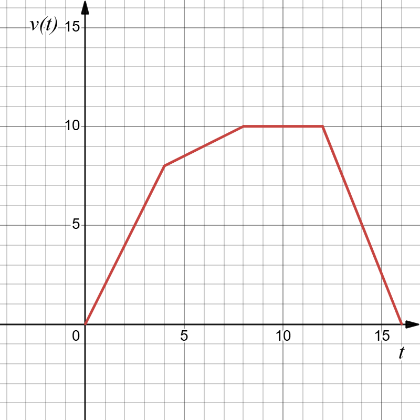
Trong khoảng thời gian từ 2s đến 14s, chất điểm nói trên di chuyển được quãng đường có độ dài bao nhiêu mét?
(nhập đáp án vào ô trống)
Đáp án đúng là: 103
Viết biểu thức vận tốc đối với từng đoạn một, sau đó lấy tích phân để tính quãng đường.
Đáp án cần điền là: 103
Xét tích phân \(I = \int\limits_{\dfrac{{ - m}}{2}}^{\dfrac{m}{2}} {\dfrac{{x - m}}{{x + m}}dx} \,\left( {m > 0} \right)\). Biết giá trị của tích phân \(I = - 3\), hãy tìm giá trị của \(m\).
Đáp án đúng là: A
Tính tích phân đã cho theo tham số \(m\).
Đáp án cần chọn là: A
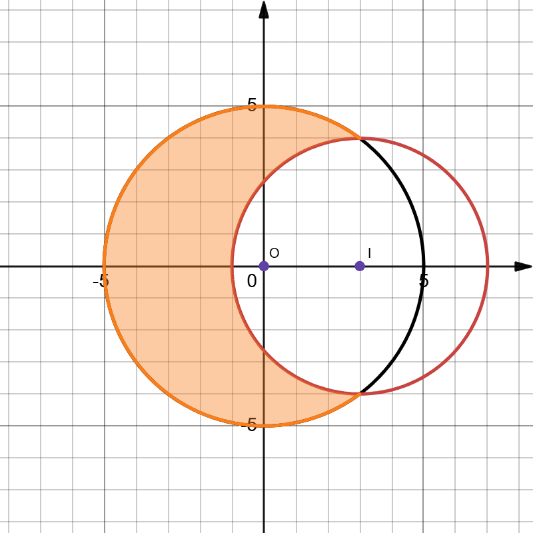
Một hình mặt trăng được tạo bởi hai đường tròn \(\left( {O;{R_1}} \right)\)và \(\left( {I;{R_2}} \right)\) (phần tô màu vàng trên hình vẽ). Biết rằng\({R_1} = 5\left( {{\rm{cm}}} \right),\,{R_2} = 4\left( {{\rm{cm}}} \right),OI = 3\left( {{\rm{cm}}} \right)\). Diện tích của hình mặt trăng được tô màu vàng là: (làm tròn kết quả tới chữ số hàng phần trăm):
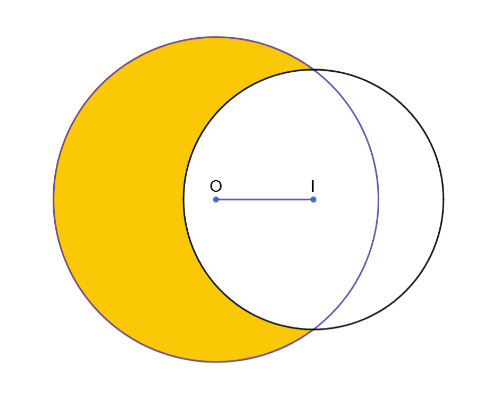
Đáp án đúng là: A
Gắn hệ trục toạ độ cho hình vẽ.
Đáp án cần chọn là: A
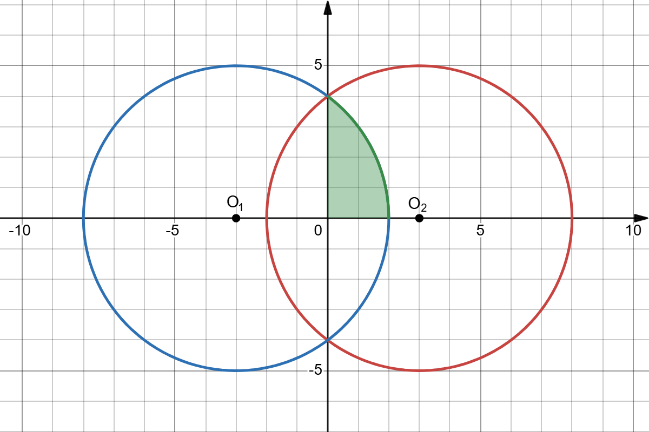
Cho 2 hình cầu như hình vẽ. Biết rằng bán kính của hai hình cầu đều bằng 5, khoảng cách giữa tâm của hai hình cầu bằng 6. Thể tích phần chung giữa 2 hình cầu là \({V_C} = \dfrac{a}{b}\pi \) (\(\dfrac{a}{b}\) là phân số tối giản, \(a,\,b > 0\)). Giá trị của biểu thức \(T = ab\) bằng bao nhiêu? (nhập đáp án vào ô trống)
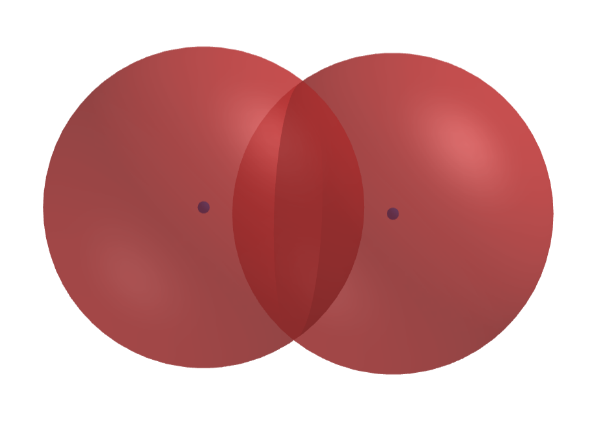
Đáp án đúng là: 312
Gắn hệ trục toạ độ cho hình vẽ.
Đáp án cần điền là: 312
Trong một đợt kiểm tra vệ sinh an toàn thực phẩm của ngành y tế tại chợ X, ban quản lý chợ lấy ra \(15\) mẫu thịt lợn trong đó có 4 mẫu ở quầy A, 5 mẫu ở quầy B, 6 mẫu ở quầy C. Đoàn kiểm tra lấy ngẫu nhiên 4 mẫu để phân tích xem trong thịt lợn có chứa hóa chất tạo nạc hay không. Xác suất để mẫu thịt của cả 3 quầy A, B, C đều được chọn bằng:
Đáp án đúng là: C
Đáp án cần chọn là: C
Trong mặt phẳng với hệ tọa độ\(Oxy\), chọn ngẫu nhiên một điểm mà tọa độ là các số nguyên có giá trị tuyệt đối nhỏ hơn hay bằng 4. Nếu các điểm có cùng xác suất được chọn như nhau, vậy thì xác suất để chọn được một điểm mà khoảng cách đến gốc tọa độ nhỏ hơn hoặc bằng 2 là:
Đáp án đúng là: A
+) Biểu diễn không gian mẫu dưới dạng tập hợp \(\Omega = \left\{ {\left. {\left( {x;y} \right)} \right|\left| x \right| \le 4;\left| y \right| \le 4;x;y \in \mathbb{Z}} \right\},\)tìm \(\left| \Omega \right|\)
+) Gọi A là biến cố: “Tập hợp các điểm mà khoảng cách đến gốc tọa độ nhỏ hơn hoặc bằng 2”, biểu diễn A dưới dạng tập hợp và tìm số phần tử của A.
+) Tính xác suất của biến cố A: \(P\left( A \right) = \dfrac{{\left| A \right|}}{{\left| \Omega \right|}}\)
Đáp án cần chọn là: A
Ở một thị xã, tỉ lệ mắc căn bệnh M là 22%. Chính quyền thị xã đó muốn biết danh sách những người bị mắc bệnh nên đã tổ chức xét nghiệm cho toàn bộ người dân. Tuy nhiên bộ “test” được sử dụng trong phương pháp xét nghiệm này có những sai sót nhất định:
- Nếu một người không bị bệnh thì xác suất bộ “test” cho ra kết quả dương tính là 10%.
- Nếu bộ “test” cho ra kết quả dương tính thì xác suất bị bệnh là 70%.
Đáp án đúng là: B
Vận dụng các công thức xác suất (công thức cộng, công thức nhân, công thức xác suất toàn phần, công thức Bayes…)
Đáp án cần chọn là: B
Phần 2: Văn học - Ngôn Ngữ
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án đúng là: C
Vận dụng kiến thức đã học về nghĩa của từ
Đáp án cần chọn là: C
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án đúng là: A
Vận dụng kiến thức đã học về nghĩa của từ
Đáp án cần chọn là: A
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án đúng là: A
Vận dụng kiến thức đã học về nghĩa của từ
Đáp án cần chọn là: A
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án đúng là: A
Vận dụng kiến thức đã học về nghĩa của từ
Đáp án cần chọn là: A
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án đúng là: B
Vận dụng kiến thức đã học về nghĩa của từ
Đáp án cần chọn là: B
Chọn cặp từ/cụm từ thích hợp nhất điền vào chỗ trống:
Càng nhiều tri thức thì ________ có thêm trí tưởng tượng, và ________ càng giàu tưởng tượng thơ mộng thì sẽ nảy sinh nhiều ý tưởng bất ngờ cho sáng tạo khoa học.
Đáp án đúng là: B
Suy luận
Đáp án cần chọn là: B
Chọn cặp từ/cụm từ thích hợp nhất điền vào chỗ trống:
Những lời khuyên của Bác Hồ nhẹ nhàng mà ________ khiến người nghe luôn ________ rồi làm theo một cách tự nguyện.
Đáp án đúng là: B
Suy luận
Đáp án cần chọn là: B
Chọn cặp từ/cụm từ thích hợp nhất điền vào chỗ trống:
Có lúc bạn ________trong các loại cảm xúc hỗn độn. Bạn buồn, bạn giận dữ, bạn vui, bạn lo lắng, bạn mệt mỏi cả về thể xác và ________ vì những thứ diễn ra trong đầu.
Đáp án đúng là: A
Suy luận
Đáp án cần chọn là: A
Chọn cặp từ/cụm từ thích hợp nhất điền vào chỗ trống:
Màu sắc của tia sáng ________vào bước sóng của nó. Trong tia sáng ________, tia sáng màu tím có bước sóng ngắn nhất, tia sáng đỏ có bước sóng dài nhất.
Đáp án đúng là: D
Suy luận
Đáp án cần chọn là: D
Chọn cặp từ/cụm từ thích hợp nhất điền vào chỗ trống:
Các cơ quan trong cơ thể chỉ ________ một lần, sau khi sinh ra thì không ________ nữa. Chỉ có răng mọc hai lần.
Đáp án đúng là: B
Suy luận
Đáp án cần chọn là: B
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
“Càng lớn lên tôi càng thấy việc học trở nên nghiêm trọng, những kiến thức ngày một nhiều khiến tôi đang rất mơ hồ.”
Đáp án đúng là: B
Suy luận
Đáp án cần chọn là: B
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
“Lễ nhận chức diễn ra vô cùng long trọng và đã thành công tốt đẹp.”
Đáp án đúng là: A
Căn cứ nội dung nghĩa của từ
Đáp án cần chọn là: A
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
“Tràng giang có chất Đường thi hơn những bài thơ Đường trung đại. Chính Huy Cận cũng thừa nhận ông đã lấy cảm hứng từ ý thơ của Đỗ Phủ, Thôi Hiệu đời Đường, của Chinh phụ ngâm để cho bài thơ đạt đến tác phong cổ điển.”
Đáp án đúng là: D
Căn cứ nội dung nghĩa của từ
Đáp án cần chọn là: D
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
Không cầu kỳ như trà đạo Nhật - Chanoyu hay Gongfucha – trà đạo Trung Hoa, trà đạo Việt Nam có phần giản dị hơn trong cách pha chế. Tuy nhiên, người Việt đặc biệt là những người có kiến thức uyên thâm về trà, đặc biệt yêu cầu khắt khe về hương vị.
Đáp án đúng là: B
Căn cứ nội dung nghĩa của từ
Đáp án cần chọn là: B
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
Chủ tịch Hồ Chí Minh không chỉ là tấm gương của một vĩ nhân, một lãnh tụ cách mạng vĩ đại, ở Người còn toát lên hình ảnh một con người rất đỗi giản dị, khiêm tốn, thân thiết với nhân dân.
Đáp án đúng là: D
Căn cứ nội dung nghĩa của từ
Đáp án cần chọn là: D
Đọc đoạn trích sau đây và trả lời các câu hỏi sau:
[…] Khi bạn tức giận, bản lĩnh thể hiện khi chúng ta biết kiềm chế cảm xúc chứ không phải là hành động nông nổi. Bản lĩnh không kiểm soát được thì chỉ là sự liều lĩnh. Bên cạnh đó, nếu bản lĩnh của chúng ta làm người khác phải khó chịu thì chúng ta đã thất bại. Vì bản lĩnh đó chỉ phục vụ cá nhân mà ta không hướng đến mọi người. Bản lĩnh đúng nghĩa. Bản lĩnh là khi bạn dám nghĩ, dám làm và có thái độ sống tốt. Muốn có bản lĩnh bạn cũng phải kiên trì luyện tập. Chúng ta thường yêu thích những người có bản lĩnh sống. Bản lĩnh đúng nghĩa chỉ có được khi bạn biết đặt ra mục tiêu và phương pháp để đạt được mục tiêu đó. Nếu không có phương pháp thì cũng giống như bạn đang nhắm mắt chạy trên con đường có nhiều ổ gà. Cách thức ở đây cũng rất đơn giản. Đầu tiên, bạn phải xác định được hoàn cảnh và môi trường để bản lĩnh được thể hiện đúng lúc, đúng nơi, không tùy tiện. Thứ hai, bạn phải chuẩn bị cho mình những tài sản bổ trợ như sự tự tin, ý chí, nghị lực, quyết tâm… Điều thứ ba vô cùng quan trọng chính là khả năng của bạn. Đó là những kỹ năng đã được trau đồi cùng với vốn tri thức, trải nghiệm. Một người mạnh hay yếu quan trọng là tùy thuộc vào yếu tố này. Bản lĩnh tốt là vừa phục vụ được mục đích cá nhân vừa có được sự hài lòng từ những người xung quanh. Khi xây dựng được bản lĩnh, bạn không chỉ thể hiện được bản thân mình mà còn được nhiều người thừa nhận và yêu mến hơn.
(Trích “Xây dựng bản lĩnh cá nhân” – Nguyễn Hữu Long, http://tuoitre.vn, ngày 14/05/2012)
Trả lời cho các câu 66, 67, 68, 69, 70 dưới đây:
Theo nội dung đoạn trích, từ nào KHÔNG cùng nhóm với các từ còn lại?
Đáp án đúng là: C
Đọc kĩ đoạn văn, đối chiếu, phân tích, tổng hợp.
Đáp án cần chọn là: C
Theo tác giả, bản lĩnh đúng nghĩa chỉ có được khi nào?
Đáp án đúng là: C
Đọc kĩ đoạn văn, đối chiếu, phân tích, tổng hợp.
Đáp án cần chọn là: C
Ở phần đầu văn bản, tác giả nói về sự nông nổi, liều lĩnh để làm gì?
Đáp án đúng là: D
Đọc kĩ đoạn văn, đối chiếu, phân tích, tổng hợp.
Đáp án cần chọn là: D
Theo tác giả, sự mạnh yếu của một người phụ thuộc vào điều gì?
Đáp án đúng là: C
Đọc kĩ đoạn văn, đối chiếu, phân tích, tổng hợp.
Đáp án cần chọn là: C
Ý chính của đoạn trích là gì?
Đáp án đúng là: C
Đọc kĩ đoạn văn, đối chiếu, phân tích, tổng hợp.
Đáp án cần chọn là: C
Đọc đoạn trích sau đây và trả lời 5 câu hỏi sau:
Dù khác nhau về chiều cao, cân nặng, độ tuổi, giới tính và môi trường sống, nhưng tất cả con người đều có chung một đặc điểm là nhiệt độ cơ thể luôn ở mức khoảng 37 độ C. Về cơ bản, trong tổng số năng lượng của cơ thể người và các loài động vật có vú, trên 70% được chuyển hóa thành nhiệt, phát tán ra môi trường. Nếu không phát tán, nhiệt tích tụ sẽ gây hiện tượng quá nóng, làm đình trệ các hoạt động bình thường của cơ thể. Tuy nhiên, dù nhiệt được sản sinh ra ở trạng thái đỉnh điểm thì cơ thể vẫn luôn được giữ ổn định, bởi vì nhiệt sản sinh ra được não điều khiển để cân bằng với nhiệt bài tiết ra môi trường. Căn cứ vào nguyên lí truyền nhiệt, các nhà khoa học đã giải thích rằng với các dạng khí hậu, môi trường sống như hiện nay của trái đất thì nhiệt độ bình quân của cơ thể người khoảng 37 độ C là phù hợp với tỷ suất sản sinh và phát tán nhiệt của cơ thể, sao cho thích ứng được với mọi loại thời tiết và thích ứng cho não cũng như các cơ quan đạt hiệu suất hoạt động cao nhất.
(Đức Anh, 10 vạn câu hỏi vì sao, NXB Dân trí, 2016, tr.96)
Trả lời cho các câu 71, 72, 73, 74, 75 dưới đây:
Theo văn bản, cơ thể luôn được giữ ổn định là nhờ vào điều gì?
Đáp án đúng là: D
Đọc văn bản, tìm ý.
Đáp án cần chọn là: D
Khi nhiệt độ cơ thể ở mức khoảng 37 độ C, tác dụng nào KHÔNG phù hợp?
Đáp án đúng là: D
Đọc văn bản, tìm ý.
Đáp án cần chọn là: D
Thông tin nào sau đây KHÔNG THỂ suy ra từ nội dung của văn bản?
Đáp án đúng là: A
Đọc văn bản, tìm ý.
Đáp án cần chọn là: A
Theo văn bản, thông tin nào KHÔNG đúng về nhiệt độ cơ thể của con người?
Đáp án đúng là: C
Đọc văn bản, tìm ý.
Đáp án cần chọn là: C
Ý chính của văn bản là gì?
Đáp án đúng là: B
Đọc văn bản, tìm ý.
Đáp án cần chọn là: B
Đọc đoạn trích dưới đây và trả lời câu hỏi:
Ngược lại với những kỳ vọng về sự hoàn hảo ở đứa trẻ, trong xã hội hiện đại, nhiều phụ huynh lo sợ con mình chịu áp lực, nên đã chủ trương để con thoải mải chơi là chính, không quan trọng việc học tập và rèn luyện để đạt thành tích tốt. Tôi cũng không đồng ý với quan điểm này. Bởi vì cuộc đời đứa trẻ rất dài, bố mẹ chỉ ở bên con cho đến tuổi trưởng thành. Khi bước vào đại học, các em sẽ phải va vấp xã hội. Lúc này bố mẹ không thể kiểm soát và giám sát. Trên con đường lập nghiệp, sẽ có rất nhiều áp lực, thậm chí là áp lực khủng khiếp. Để trẻ vượt qua những áp lực trên con đường đó thì chẳng cách nào tốt hơn là cha mẹ phải dạy trẻ “tự lái” ngay từ khi còn nhỏ.
Bản chất của áp lực là dương, nên cuộc sống luôn phải có một số áp lực. Một đứa trẻ không vượt qua nổi áp lực, sau này lớn lên, tôi tin đứa trẻ đó sẽ rất khó thành công trong cuộc sống. Nhưng có áp lực chịu được, có áp lực độc hại. Với một đứa trẻ, để dạy chúng “tự lái”, cha mẹ nên biết tạo áp lực vừa phải, đủ giúp chúng kiểm soát tốt bản thân và để cha mẹ hiểu tâm sinh lý, khả năng của con nhằm đồng hành với chúng.
(Áp lực thành tích - Trần Văn Phúc, Vnexpress, Thử bay. 18/12/2021)
Phương thức biểu đạt chính của đoạn trích là gì?
Đáp án đúng là: C
Vận dụng kiến thức đã học về phương thức biểu đạt
Đáp án cần chọn là: C
Đọc đoạn trích dưới đây và trả lời câu hỏi:
Chúng ta ai cũng khao khát thành công. Tuy nhiên, mỗi người định nghĩa thành công theo cách riêng. Có người gắn thành công với sự giàu có về tiền bạc, quyền lực, tài cao học rộng; có người lại cho rằng một gia đình êm ấm, con cái nên người là thành công…Chung quy lại, có thể nói thành công là đạt được những điều mong muốn, hoàn thành mục tiêu của mình.
(Theo Lê Minh – Sống hạnh phúc)
Biện pháp tu từ nghệ thuật nào được sử dụng trong câu văn: “Có người gắn thành công với sự giàu có về tiền bạc, quyền lực, tài cao học rộng; có người lại cho rằng một gia đình êm ấm, con cái nên người là thành công…”?
Đáp án đúng là: C
Căn cứ nội dung về biên pháp tu từ
Đáp án cần chọn là: C
Đọc đoạn thơ và trả lời câu hỏi dưới đây:
Cô gái như chùm hoa lặng lẽ
Nhờ hương thơm nói hộ tình yêu
(Anh vô tình anh chẳng biết điều
Tôi đã đến với anh rồi đấy)
(Trích “Hương thầm” – Phan Thị Thanh Nhàn)
Ý nào nêu đúng tác dụng của phép tu từ chêm xen trong đoạn thơ trên?
Đáp án đúng là: A
Căn cứ nội dung đoạn thơ
Đáp án cần chọn là: A
Đọc bài ca dao sau đây và trả lời câu hỏi:
“Gió đưa cành trúc la đà
Tiếng chuông Trấn Võ canh gà Thọ Xương
Mịt mù khói tỏa ngàn sương
Nhịp chày Yên Thái, mặt gương Tây Hồ”
Hình ảnh so sánh “canh gà” trong bài ca dao được hiểu là:
Đáp án đúng là: C
Căn cứ nội dung bài đọc.
Đáp án cần chọn là: C
Đọc đoạn trích và trả lời câu hỏi dưới đây:
“Sau này tôi đi lập nghiệp phương Nam, mùa thị chín chỉ theo về trong những giấc mơ sầu xứ. Cho nên chiều hôm qua, rổ thị bày bất chợt bên chợ ven đường đã buộc tôi dừng chân, 'ngoái đầu thương dĩ vãng'. Dĩ nhiên tôi đã mua hết rổ thị đó, không ngập ngừng, không trả giá. Bởi tôi không mua một món hàng. Tôi mua kỉ niệm. Từ một bà già đến từ ngoại ô và hẳn trong khu vườn của chủ nhân có một cây thị hiếm hoi ở đất Sài Gòn.”
(Nguyễn Nhật Ánh, Sương khói quê nhà)
Hình ảnh được miêu tả tập trung trong đoạn trích là gì?
Đáp án đúng là: A
Căn cứ nội dung bài đọc.
Đáp án cần chọn là: A
Đọc đoạn trích và trả lời câu hỏi dưới đây:
Bình minh diễn ra chỉ trong khoảng khắc. Ở đồng cỏ mênh mông cũng giống ngoài biển cả, mặt trời lên nhanh vùn vụt. Thoạt đầu nó chậm rãi nhô lên, đỏ hồng như một trái dưa hấu mới bổ, rồi sau khi vượt khỏi đường chân trời chắn ngang, nó leo mau lên cao và nắng chợt chói chang lúc nào không hay.
(Trích Tuyển tập truyện thiếu nhi – Vũ Hùng)
Đối tượng chính được miêu tả trong đoạn trích là gì?
Đáp án đúng là: D
Căn cứ nội dung bài đọc
Đáp án cần chọn là: D
Đọc đoạn trích và trả lời câu hỏi dưới đây:
Dòng sông lặng ngắt như tờ,
Sao đưa thuyền chạy, thuyền chờ trăng theo.
Bốn bề phong cảnh vắng teo,
Chỉ nghe cót két tiếng chèo thuyền nan.
Lòng riêng riêng những bàn hoàn,
Lo sao khôi phục giang san Tiên Rồng.
Thuyền về, trời đã rạng đông,
Bao la nhuốm một màu hồng đẹp tươi.
(Đi thuyền trên sông Đáy – Hồ Chí Minh)
Từ “bàn hoàn” trong đoạn trích trên có ý nghĩa gì?
Đáp án đúng là: C
Đọc đoạn trích
Đáp án cần chọn là: C
Đọc đoạn trích và trả lời câu hỏi dưới đây:
“Vì sao trái đất nặng ân tình
Nhắc mãi tên người Hồ Chí Minh.”
(Tố Hữu)
Hình ảnh “trái đất” trong đoạn trích trên thể hiện điều gì?
Đáp án đúng là: C
Đọc đoạn trích
Đáp án cần chọn là: C
Đọc đoạn trích và trả lời câu hỏi dưới đây:
Tháo nói:
- Anh hùng là người trong bụng có chí lớn, có mưu cao, có tài bao trùm được cả vũ trụ, có chí nuốt cả trời đất kia.
Huyền Đức mới hỏi:
- Ai có thể xứng đáng được như thế?
Tháo lấy tay trỏ vào Huyền Đức, rồi lại trỏ vào mình nói rằng:
- Anh hùng trong thiên hạ bây giờ chỉ có sứ quân và Tháo mà thôi.
Huyền Đức nghe nói giật nảy mình, bất giác thìa, đũa cầm ở tay rơi cả xuống đất. Đúng lúc ấy, cơn mưa sắp đến, có một tiếng sấm rền vang. Huyền Đức ung dung cúi xuống nhặt đũa và thìa, nói tảng rằng:
- Gớm thật! Tiếng sấm dữ quá!
Tháo cười hỏi rằng:
- Trượng phu cũng sợ sấm à?
Huyền Đức nói:
- Đức thánh ngày xưa gặp lúc sấm dữ gió to cũng đổi sắc mặt, sao tôi lại không sợ!
Huyền Đức đã che đậy được hết việc mình đánh rơi cả thìa đũa khi nghe Tháo gọi mình là anh hùng.
Tháo thấy thế không nghi ngờ gì Huyền Đức nữa.
(Trích Tam quốc diễn nghĩa – La Quán Trung)
Đoạn trích trên thể hiện phẩm chất gì của nhân vật Huyền Đức?
Đáp án đúng là: A
Đọc đoạn trích
Đáp án cần chọn là: A
Đọc đoạn trích sau đây và trả lời các câu hỏi:
“Việt tỉnh dậy lần thứ tư, trong đầu còn thoáng qua hình ảnh của người mẹ. Đêm nữa lại đến. Đêm sâu thăm thẳm, bắt đầu từ tiếng dế gáy u u cao vút mãi lên. Người Việt như đang tan ra nhè nhẹ… Ở đó có các anh đang chờ Việt, đạn ta đang đổ lên đầu giặc Mĩ những đám lửa dữ dội, và những mũi lê nhọn hoắt trong đêm đang bắt đầu xung phong”
(Những đứa con trong gia đình – Nguyễn Thi, Ngữ văn 12, Tập hai, NXB Giáo dục)
Đoạn trích trên thể hiện phẩm chất gì của nhân vật Việt?
Đáp án đúng là: D
Căn cứ nội dung bài đọc.
Đáp án cần chọn là: D
Đọc đoạn trích dưới đây và trả lời các câu hỏi từ 86 đến 90:
Búp bê Barbie mà chúng ta thường chơi khi còn nhỏ đã cung cấp tiêu chuẩn về cái đẹp dành cho nữ giới. Búp bê Barbie có cơ thể gần như là phi thực tế, nhưng rất nhiều phụ nữ lớn lên với niềm tin đó là cơ thể lý tưởng và lao vào cuộc chiến sắc đẹp khốc liệt.
Sắc đẹp là thứ chỉ ít người có và không phải ai cũng có thể duy trì mãi mãi. Thế nhưng xã hội này lại tích cực khuyến khích phụ nữ khao khát và mong muốn mình ngày càng đẹp hơn. Các chương trình truyền hình hay quảng cáo ca ngợi những người phụ nữ xinh đẹp, trẻ trung, mình hạc xương mai và còn coi đó là chuẩn mực cho hành động nữ tính hay một kiểu phát triển bản thân. Cuộc cạnh tranh sắc đẹp là một trong số ít những cuộc cạnh tranh công khai dành cho nữ giới, vậy nên họ có thể cạnh tranh dữ dội, khốc liệt mà không phải chịu sự kìm kẹp của xã hội.
Cuộc cạnh tranh về cái đẹp đã lan sang cả thế hệ thanh thiếu niên. Thời gian gần đây, thế hệ 10X cũng trang điểm đậm, sửa đồng phục để lộ cơ thể. Điều đáng ngạc nhiên là sự làm dáng này không nhằm mục đích để nam giới ngắm nhìn. Theo tạp chí Siddeutsche zeitung của Đức, số học sinh nữ ý thức về nam giới và trang điểm chỉ chiếm khoảng 10%. Điều các học sinh nữ coi trọng không phải là ánh nhìn của nam sinh mà là cuộc cạnh tranh sắc đẹp giữa các bạn đồng trang lứa.
(Trích “Góc khuất yêu thương”, Choi Kwanghyun)
Trả lời cho các câu 86, 87, 88, 89, 90 dưới đây:
Ý nào KHÔNG là nguyên nhân dẫn đến cuộc cạnh tranh sắc đẹp?
Đáp án đúng là: D
Căn cứ văn bản
Đáp án cần chọn là: D
Tác dụng của việc nhắc đến tạp chí Siddeutsche zeitung là gì?
Đáp án đúng là: B
Căn cứ văn bản
Đáp án cần chọn là: B
Nội dung chính của đoạn trích trên là gì?
Đáp án đúng là: D
Căn cứ nội dung bài đọc.
Đáp án cần chọn là: D
Theo đoạn trích, hệ quả nghiêm trọng của cuộc cạnh tranh sắc đẹp trong giới nữ là gì?
Đáp án đúng là: D
Căn cứ nội dung bài đọc.
Đáp án cần chọn là: D
Phương thức biểu đạt chính của đoạn trích là gì?
Đáp án đúng là: C
Căn cứ nội dung bài đọc
Đáp án cần chọn là: C
Đọc đoạn trích dưới đây và trả lời các câu hỏi từ 91 đến 95:
Con còn bế trên tay
Con chưa biết con cò
Nhưng trong lời mẹ hát
Có cánh cò đang bay:
“Con cò bay la
Con cò bay lả
Con cò Cổng Phủ
Con cò Đồng Đăng…”
Cò một mình, cò phải kiếm lấy ăn
Con có mẹ, con chơi rồi lại ngủ”
Con cò ăn đêm
Con cò xa tổ
Cò gặp cành mềm
Cò sợ xáo măng…”
Ngủ yên, ngủ yên, cò ơi, chớ sợ
Cành có mềm, mẹ đã sẵn tay nâng
Trong lời ru của mẹ thấm hơi xuân
Con chưa biết con cò con vạc
Con chưa biết những cành mềm mẹ hát
Sữa mẹ nhiều, con ngủ chẳng phân vân.
(Trích "Con cò", Chế Lan Viên)
Trả lời cho các câu 91, 92, 93, 94, 95 dưới đây:
Nội dung của những câu thơ trong ngoặc kép gợi nhắc đến những tác phẩm thuộc thể loại nào trong văn học dân gian?
Đáp án đúng là: B
Căn cứ nội dung bài đọc
Đáp án cần chọn là: B
Nhân vật trữ tình trong đoạn trích trên là ai?
Đáp án đúng là: C
Căn cứ nội dung bài đọc.
Đáp án cần chọn là: C
Hình ảnh con cò trong đoạn trích là biểu trưng cho điều gì?
Đáp án đúng là: A
Căn cứ nội dung bài đọc.
Đáp án cần chọn là: A
Nghĩa của câu thơ “Cành có mềm, mẹ đã sẵn tay nâng” là gì?
Đáp án đúng là: A
Căn cứ nội dung bài đọc.
Đáp án cần chọn là: A
Nội dung chính của đoạn trích là gì?
Đáp án đúng là: B
Căn cứ nội dung bài đọc
Đáp án cần chọn là: B
Đọc đoạn trích dưới đây và trả lời các câu hỏi từ 96 đến 100:
Tiếng Việt mình sâu sắc. Nhân là con người. Nhân cũng là hạt. Nhân cũng là lòng yêu thương người khác. Nhìn những anh chị bại liệt cũng trở thành hiệp sĩ công nghệ thông tin giúp đời. Biết những người khiếm thị cũng làm được nghề sửa chữa điện tử, để có ích và giúp người. Lòng tự hứa không thể là hạt lép. Chẳng có lí do gì để không là hạt giống tốt cho mùa sau.
Từ đó ta có bài học về nết tốt của hạt: Kiên trì, nhẫn nại, và lòng dũng cảm. Cũng như ta học về việc sống hết mình của hạt thóc: sớm cho mùa vàng, dám chịu xay giã giần sàng. Gạo nuôi người, cám bã nuôi heo, rơm tặng người bạn trâu. Và đến cọng rơm thừa cũng bện thành con cúi giữ lửa suốt đêm trường. Và sưởi ấm cánh đồng mùa đông gió bấc.
Mỗi khi ta cằn cỗi, hãy nhớ ta là hạt. Ta lại nghĩ về khoảng xanh ngoài ban công, cũng như bạn thấy những mầm cây đội lên từ khối bê tông đường nhựa. Để không cho những khiếm khuyết tự bào mòn hay những nỗi buồn tự hủy.
(Trích "Gửi em mây trắng", Đoàn Công Lê Huy)
Trả lời cho các câu 96, 97, 98, 99, 100 dưới đây:
Phương thức biểu đạt chính của đoạn trích là gì?
Đáp án đúng là: D
Căn cứ nội dung bài đọc
Đáp án cần chọn là: D
Theo tác giả, ta học được bài học gì từ hạt?
Đáp án đúng là: B
Căn cứ nội dung bài đọc.
Đáp án cần chọn là: B
Giọng điệu chủ đạo của đoạn trích là gì?
Đáp án đúng là: C
Căn cứ nội dung bài đọc.
Đáp án cần chọn là: C
Biện pháp tu từ nghệ thuật nào được sử dụng trong câu “Lòng tự hứa không thể là hạt lép”?
Đáp án đúng là: A
Căn cứ nội dung bài đọc.
Đáp án cần chọn là: A
Ý nào sau đây thể hiện chính xác nhất điều tác giả muốn nói trong đoạn trích?
Đáp án đúng là: C
Căn cứ nội dung bài đọc
Đáp án cần chọn là: C