Phần 1: Tư duy Toán học
Tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{2x + 1}}{{3x - 1}}\) là đường thẳng có phương trình
Đáp án đúng là: D
Tiệm cận ngang của đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\,\,\left( {ad - bc \ne 0,\,\,c \ne 0} \right)\) là \(y = \dfrac{a}{c}\).
Đáp án cần chọn là: D
Trong không gian \(Oxyz\), đường thẳng \(d:\dfrac{{x - 1}}{2} = \dfrac{{y - 2}}{{ - 1}} = \dfrac{{z + 3}}{{ - 2}}\) có 1 vectơ chỉ phương là
Đáp án đúng là: A
Phương trình chính tắc của đường thẳng đi qua \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có 1 VTCP \(\overrightarrow u \left( {a;b;c} \right),\,\,\left( {a,b,c \ne 0} \right)\) là: \(\dfrac{{x - {x_0}}}{a} = \dfrac{{y - {y_0}}}{b} = \dfrac{{z - {z_0}}}{c}\).
Đáp án cần chọn là: A
Đạo hàm của hàm số \(y = \cos x\) trên \(\mathbb{R}\) là
Đáp án đúng là: D
Sử dụng bảng đạo hàm cơ bản.
Đáp án cần chọn là: D
Cho khối lập phương có thể tích bằng 2. Cạnh của khối lập phương đã cho bằng
Đáp án đúng là: C
Thể tích khối lập phương cạnh a là \({a^3}\).
Đáp án cần chọn là: C
Trong không gian \(Oxyz\), hình chiếu vuông góc của điểm \(M\left( {1;2;3} \right)\) lên mặt phẳng \(\left( {Oxy} \right)\) là điểm
Đáp án đúng là: C
Hình chiếu vuông góc của điểm \(M\left( {x;y;z} \right)\) lên mặt phẳng \(\left( {Oxy} \right)\) là điểm \(M'\left( {x;y;0} \right)\).
Đáp án cần chọn là: C
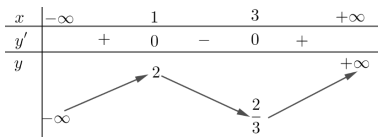
Cho hàm số $y=\dfrac{x^3}{3}-2 x^2+3 x+\dfrac{2}{3}$ có đồ thị $(C)$. Xét tính đúng sai của các mệnh đề:
| Đúng | Sai | |
|---|---|---|
| a) Hàm số đã cho có hai điểm cực trị. | ||
| b) Giá trị cực tiểu của hàm số là $x=3$ | ||
| c) Điểm cực đại của đồ thị hàm số đã cho là $x=1$. | ||
| d) Khoảng cách giữa hai điểm cực trị của đồ thị hàm số đã cho là $\dfrac{2\sqrt{13}}{3}$. |
Đáp án đúng là: Đ; S; S; Đ
Đáp án cần chọn là: Đ; S; S; Đ
Cho các hàm số \(f\left( x \right),g\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;4} \right]\). Nếu \(\int\limits_{ - 1}^4 {f\left( x \right)dx} = 2\) và \(\int\limits_{ - 1}^4 {g\left( x \right)dx} = 3\) thì \(\int\limits_{ - 1}^4 {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} \) bằng
Đáp án đúng là: D
\(\int\limits_a^b {\left[ {f\left( x \right) \pm g\left( x \right)} \right]dx} = \int\limits_a^b {f\left( x \right)dx} \pm \int\limits_a^b {g\left( x \right)dx} \).
Đáp án cần chọn là: D
Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 2x - 4y - 6z + 1 = 0\). Bán kính của \(\left( S \right)\) là
Đáp án đúng là: A
Mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) có tâm \(I\left( {a;b;c} \right)\), bán kính \(R = \sqrt {{a^2} + {b^2} + {c^2} - d} \), trong đó \({a^2} + {b^2} + {c^2} - d > 0\).
Đáp án cần chọn là: A
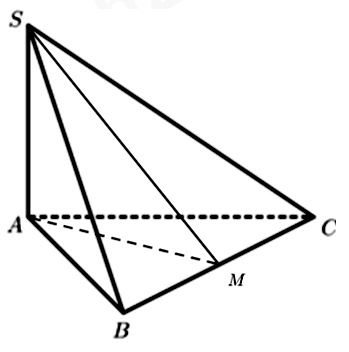
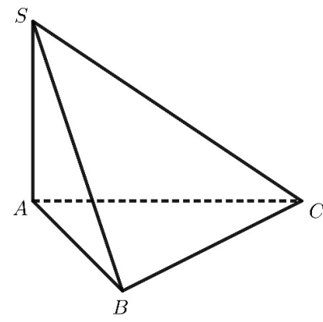
Cho khối chóp \(S.ABC\) có đáy là tam giác vuông tại \(A,\,AB = 2,AC = 4;\,\,SA\) vuông góc với đáy và \(SA = 3\) (tham khảo hình vẽ).
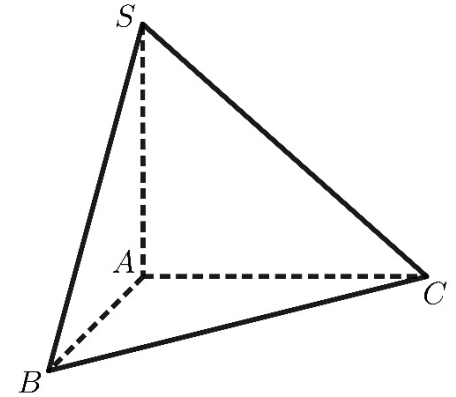
Thể tích của khối chóp đã cho bằng
Đáp án đúng là: D
Công thức thể tích khối tứ diện vuông với độ dài ba cạnh góc vuông là \(a,b,c\) là: \(V = \dfrac{1}{6}abc\).
Đáp án cần chọn là: D
Cho cấp số cộng \(\left( {{u_n}} \right)\) với \({u_1} = 2,{u_3} = 6\). Công sai của cấp số cộng này bằng
Đáp án đúng là: B
Số hạng tổng quát của cấp số cộng có số hạng đầu \({u_1}\) và công sai \(d\) là \({u_n} = {u_1} + \left( {n - 1} \right)d,\,\,n \in {\mathbb{N}^*}\).
Đáp án cần chọn là: B
Bảng dưới đây thống kê cự li ném tạ của một vận động viên.

Hãy tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên (kết quả được làm tròn đến hàng phần trăm)
Đáp án đúng là: 0,53
Đáp án cần điền là: 0,53
Tổng tất cả các nghiệm của phương trình \({2^x} = 3x - 1\) bằng
Đáp án đúng là: B
Sử dụng tính đơn điệu của hàm số để đánh giá.
Đáp án cần chọn là: B
Trong hình dưới, khi được kéo ra khỏi vị trí cân bằng ở điểm O và buông tay, lực đàn hồi của lò xo khiến vật A gắn ở đầu của lò xo dao động quanh O. Toạ độ \(s(\;{\rm{cm}})\) của A trên trục Ox vào thời điểm t (giây) sau khi buông tay được xác định bởi công thức \(s = 10\sin \left( {10t + \dfrac{\pi }{2}} \right)\). Trong 10 giây đầu tiên thì vật đi qua vị trí \(s = - 5\sqrt 3 \;{\rm{cm}}\) bao nhiêu lần?
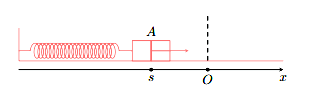
Đáp án đúng là: 100
Đáp án cần điền là: 100
Cho hình chóp \(S.ABC\) có đáy là tam giác đều, \(SA\) vuông góc với đáy và \(AB = 2SA\).
Góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\) bằng
Đáp án đúng là: B
Xác định góc giữa hai mặt phẳng \(\left( \alpha \right),\,\,\left( \beta \right)\):
Tìm giao tuyến \(\Delta \) của \(\left( \alpha \right),\,\,\left( \beta \right)\).
Xác định 1 mặt phẳng \(\left( \gamma \right) \bot \Delta \).
Tìm các giao tuyến \(a = \left( \alpha \right) \cap \left( \gamma \right),b = \left( \beta \right) \cap \left( \gamma \right)\)
- Góc giữa hai mặt phẳng \(\left( \alpha \right),\,\,\left( \beta \right)\): \(\left( {\left( \alpha \right);\left( \beta \right)} \right) = \left( {a;b} \right)\)
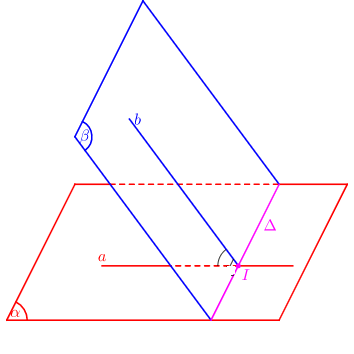
Đáp án cần chọn là: B
Khai triển nhị thức \({\left( {a - 2b} \right)^5}\) thành tổng các đơn thức
Đáp án đúng là: D
Đáp án cần chọn là: D
Trong không gian $Oxyz$, cho hai điểm $A(4 ; 2 ; 1), B(-2 ;-1 ; 4)$. Gọi $M$ là điểm thỏa mãn đẳng thức $\overrightarrow{AM}=2 \overrightarrow{MB}$. Tìm độ dài vectơ $\overrightarrow{OM}$.
Đáp án đúng là: 3
Đáp án cần điền là: 3
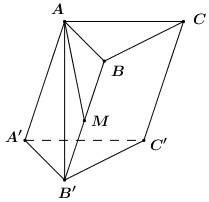
Cho hình lăng trụ \(ABC.A'B'C'\), \(M\) là trung điểm của \(BB'\). Đặt \(\overrightarrow {CA} = \overrightarrow a ,\) \(\overrightarrow {CB} = \overrightarrow b ,\) \(\overrightarrow {AA'} = \overrightarrow c \). Khẳng định nào sau đây đúng ?
Đáp án đúng là: D
Sử dụng công thức trung điểm: \(\overrightarrow {AM} = \dfrac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AB'} } \right)\) và công thức hình bình hành: \(\overrightarrow {AB'} = \overrightarrow {AB} + \overrightarrow {AA'} \).
Đáp án cần chọn là: D
Một chiếc xe ô tô đang chạy trên đường cao tốc với vận tốc \(72km/h\) thì tài xế bất ngờ đạp phanh làm cho chiếc ô tô chuyển động chậm với gia tốc \(a\left( t \right) = - \dfrac{8}{5}t{\rm{ }}\left( {m/{s^2}} \right)\), trong đó \(t\) là thời gian tính bằng giây. Hỏi kể từ khi đạp phanh đến khi ô tô dừng hẳn thì ô tô di chuyển bao nhiêu mét \(\left( m \right)\)? (Giả sử trên đường ô tô di chuyển không có gì bất thường).
Đáp án đúng là: 200/3
Đáp án cần điền là: 200/3
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên dưới
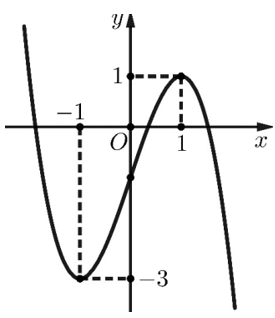
Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(2f\left( x \right) = m\) có ba nghiệm thực phân biệt?
Đáp án đúng là: C
Số nghiệm của phương trình \(f\left( x \right) = m\) bằng số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = m\).
Đáp án cần chọn là: C
Phỏng vấn một số học sinh khối 11 về thời gian (giờ) ngủ của một buổi tối, thu được bảng số liệu sau:

Hãy cho biết \(75\% \) học sinh khối 11 ngủ nhiều nhất bao nhiêu giờ?
Đáp án đúng là: 7,2
Đáp án cần điền là: 7,2
Trong không gian \(Oxyz\), cho hai điểm \(M\left( {1; - 1; - 1} \right)\) và \(N\left( {5;5;1} \right)\). Mặt phẳng \(\left( {OMN} \right)\) có phương trình là
Đáp án đúng là: A
Phương trình mặt phẳng đi qua \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có 1 VTPT \(\overrightarrow n \left( {a;b;c} \right) \ne \overrightarrow 0 \) là:
\(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) + c\left( {z - {z_0}} \right) = 0\).
Đáp án cần chọn là: A
Trong khoảng thời gian từ ngày 01/01/2024 đến hết ngày 30/09/2024, nhóm nghiên cứu đã quan sát sự phát triển của một quần thể sinh vật X. Kết quả nghiên cứu chỉ ra rằng, tại ngày thứ t của năm 2024 (tính từ ngày 01/01/2024) số cá thể sinh vật X trong quần thể được ước lượng bởi hàm số \(f\left( t \right) = - \dfrac{1}{{300}}{t^3} + b{t^2} + ct + 12000\)(con), \(0 \le t \le 365\) và ngày 26/09/2024 là ngày có số lượng cá thể sinh vật X nhiều nhất với 55740 con. Ngày 26/10/2024 số lượng cá thể sinh vật X được ước lượng khoảng bao nhiêu nghìn con? (kết quả làm tròn tới hàng phần chục)
Đáp án đúng là: 54,3
Đáp án cần điền là: 54,3
Diện tích hình phẳng giới hạn bởi các đường \(y = {x^2} - 4x + 3,x = 0\) và \(y = 0\) bằng
Đáp án đúng là: D
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\), trục hoành và hai đường thẳng \(x = a,\,x = b\) được xác định : \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \).
Đáp án cần chọn là: D
Gieo đồng thời 2 con súc sắc cân đối đồng chất.
| Đúng | Sai | |
|---|---|---|
| a) a) Số phần tử của không gian mẫu là 36 . |
||
| b) b) Số phần tử của biến cố A : " Số chấm xuất hiện trên hai con súc sắc là như nhau" bằng 3 . |
||
| c) c) Xác suất của biến cố B: "Ít nhất một con súc sắc suất hiện mặt 6 chấm" là \(\dfrac{{13}}{{36}}\) |
||
| d) d) Xác suất để C: "Số chấm suất hiện trên hai con súc sắc hơn kém nhau 2" là \(\dfrac{2}{9}\). |
Đáp án đúng là: Đ; S; S; Đ
Đáp án cần chọn là: Đ; S; S; Đ
Có bao nhiêu số tự nhiên có 5 chữ số phân biệt, trong đó có mặt cả hai chữ số 2 và 3?
Đáp án đúng là: A
- Chọn vị trí đặt 2 và 3.
- Lấy thêm 3 chữ số khác, sắp xếp vào các vị trí còn lại (chú ý vị trí của số 0).
Đáp án cần chọn là: A
Nếu \({2^x} + {2^{ - x}} = 5\) thì giá trị của biểu thức \(A = {4^x} + {4^{ - x}} + 3\) là
Đáp án đúng là: D
Bình phương 2 vế. Tính \({4^x} + {4^{ - x}}\).
Đáp án cần chọn là: D
Từ 20 học sinh ưu tủ gồm 10 nam và 10 nữ, người ta muốn thành lập một đoàn đại biểu gồm 6 người để tham dự một buổi hội thảo, trong đó có 1 trưởng đoàn là nam và 2 phó đoàn là nữ. Hỏi có bao nhiêu cách thành lập một đoàn đại biểu như vậy?
Đáp án đúng là: B
- Tìm số cách chọn 1 trưởng đoàn là nam.
- Tìm số cách chọn 2 phó đoàn là nữ.
- Tìm số cách chọn 3 người còn lại.
- Áp dụng quy tắc nhân.
Đáp án cần chọn là: B
Cho hàm số \(f(x)=\left\{\begin{array}{ll}\dfrac{x^2-1}{x-1} & \text {khi} x \neq 1 \\ x+1 & \text {khi} x=1\end{array}\right.\) và \(g(x)=4 x^2-x+1\). Khi đó:
| Đúng | Sai | |
|---|---|---|
| a) \(f(1)=2\) | ||
| b) Hàm số \(f(x)\) liên tục tại điểm \(x_0=1\) | ||
| c) Hàm số \(g(x)\) liên tục tại điểm \(x_0=1\) | ||
| d) Hàm số \(y=f(x)-g(x)\) không liên tục tại điểm \(x_0=1\) |
Đáp án đúng là: Đ; Đ; Đ; S
Đáp án cần chọn là: Đ; Đ; Đ; S
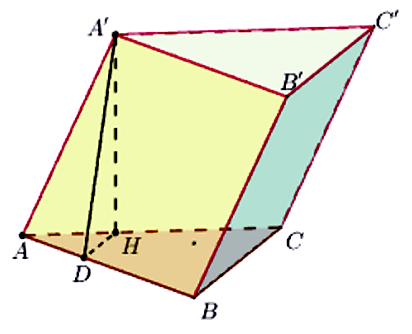
Cho khối lăng trụ \(ABC.A'B'C'\) có đáy là tam giác vuông cân tại \(B,AB = a\sqrt 3 \). Hình chiếu vuông góc của \(A'\) lên mặt phẳng \(\left( {ABC} \right)\) là điểm \(H\) thuộc cạnh \(AC\) sao cho \(HC = 2HA\). Mặt bên \(\left( {ABB'A'} \right)\) tạo với đáy một góc \({60^0}\). Thể tích khối lăng trụ đã cho bằng
Đáp án đúng là: B
Xác định góc giữa hai mặt phẳng \(\left( \alpha \right),\,\,\left( \beta \right)\):
Tìm giao tuyến \(\Delta \) của \(\left( \alpha \right),\,\,\left( \beta \right)\).
Xác định 1 mặt phẳng \(\left( \gamma \right) \bot \Delta \).
Tìm các giao tuyến \(a = \left( \alpha \right) \cap \left( \gamma \right),b = \left( \beta \right) \cap \left( \gamma \right)\)
- Góc giữa hai mặt phẳng \(\left( \alpha \right),\,\,\left( \beta \right)\): \(\left( {\left( \alpha \right);\left( \beta \right)} \right) = \left( {a;b} \right)\)
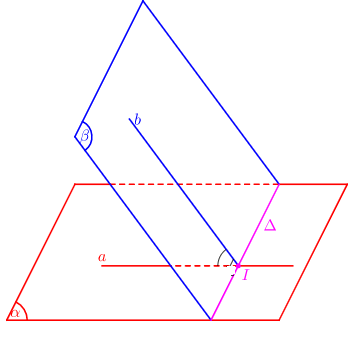
Đáp án cần chọn là: B
Dãy số dưới đây chỉ được tạo thành bởi các số 1,2 và 3: 1223331111222223333331111111…. Hỏi số thứ 100 là số nào?
Đáp án đúng là: 2
Đáp án cần điền là: 2
Có bao nhiêu giá trị nguyên của tham số \(m\) để đồ thị hàm số \(y = {x^3} - 8{x^2} + \left( {{m^2} + 11} \right)x - 2{m^2} + 2\) có hai điểm cực trị nằm về hai phía của trục hoành ?
Đáp án đúng là: B
Hàm số bậc ba có 2 điểm cực trị nằm về hai phía của trục hoành \( \Leftrightarrow \) Đồ thị hàm số cắt Ox tại 3 điểm phân biệt.
Đáp án cần chọn là: B
Trong không gian \(Oxyz\), cho hai đường thẳng \({d_1}:\dfrac{{x - 1}}{1} = \dfrac{{y + 1}}{{ - 1}} = \dfrac{z}{2}\), \({d_2}:\dfrac{x}{1} = \dfrac{{y - 1}}{2} = \dfrac{z}{1}\). Đường thẳng \(d\) đi qua điểm \(A\left( {5; - 3;5} \right)\) cắt \({d_1},{d_2}\) tại hai điểm \(B\) và \(C\). Độ dài đoạn thẳng \(BC\) là:
Đáp án đúng là: B
Tham số hóa điểm B, C theo \({d_1},{d_2}\).
Lập hpt giải t.
Tính độ dài đoạn BC.
Đáp án cần chọn là: B
Do nhu cầu đi lại của gia đình, anh Bình quyết định thực hiện tích góp tiền để mua một chiếc ôtô HONDA CRV trị giá 1,259 ti đồng.
Đợt thứ nhất: anh Bình đã tích góp theo nguyên tắc tháng sau tích góp nhiều hơn tháng ngay trước đó số tiền là 2 triệu đồng và cứ như thế đến tháng thứ 10 anh phải góp 21 triệu đồng. Đến hết đợt thứ nhất anh Bình có tất cả 624 triệu đồng.
Đọ̣t thứ hai kế tiếp: do muốn rút ngắn thời gian mua xe thì số tiền còn lại anh tiếp tục tích góp với tháng đầu là 5 triệu đồng và mỗi tháng tiếp theo số tiền gấp đôi tháng kề trước nó. Xét tính đúng sai của các khẳng định sau:
| Đúng | Sai | |
|---|---|---|
| a) Đợt thứ nhất anh Bình tích lũy tiền theo dãy số với cấp số cộng có công sai là \(d = 2\) triệu và \({u_1} = 3\) triệu. | ||
| b) Anh Bình tích lũy tiền hết đợt thứ nhất trong 25 tháng. | ||
| c) Đợt thứ hai anh Bình tích lũy tiền theo dãy số với cấp số nhân có công bội là \(q = 2\) triệu và \({u_1} = 5\) triệu. | ||
| d) Để đủ tiền mua ôtô thì anh Bình thì anh Bình tích góp ít nhất 31 tháng. |
Đáp án đúng là: Đ; S; Đ; Đ
Đáp án cần chọn là: Đ; S; Đ; Đ
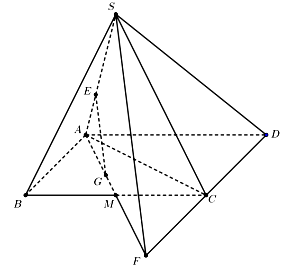
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G là trọng tâm của tam giác ABC và E là điểm thuộc cạnh SA thỏa mãn \(SE = \dfrac{m}{n} \cdot SA\) với \(\dfrac{m}{n}\) là phân số tối giản. Biết rằng GE song song với mặt phẳng (SCD). Giá trị của m.n bằng bao nhiêu?
Đáp án đúng là: 6
Đáp án cần điền là: 6
Trong lớp 12X có 45% học sinh thích học môn Toán, 40% học sinh thích học môn Ngữ Văn và 30% học sinh thích học cả hai môn Toán và Ngữ Văn. Giáo viên chủ nhiệm chọn ngẫu nhiên một học sinh trong lớp 12X.
a) Xác suất chọn được học sinh thích học môn Ngữ Văn là
b) Xác suất chọn được học sinh thích học ít nhất một trong hai môn Toán và Ngữ Văn là
c) Xác suất chọn được học sinh chỉ thích học môn Toán mà không thích học môn Ngữ Văn là
d) Xác suất chọn được học sinh thích học cả hai môn Toán và Ngữ Văn là
Đáp án đúng là: 0,4; 0,55; 0,15; 0,3
Đáp án cần chọn là: 0,4; 0,55; 0,15; 0,3
Một bình đựng 50 viên bi có kích thước, chất liệu như nhau, trong đó có 30 viên bi xanh và 20 viên bi trắng. Lấy ngẫu nhiên ra một viên bi, rồi lại lấy ngẫu nhiên ra một viên bi nữa. Tính xác suất để lấy được một viên bi xanh ở lần thứ nhất và một viên bi trắng ở lần thứ hai (làm tròn kêt quả đến chữ số thập phân thứ 2).
Đáp án đúng là: 0,24
Đáp án cần điền là: 0,24
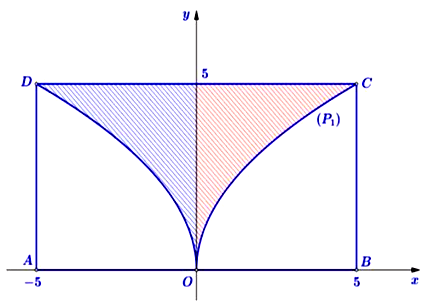
Từ hình chữ nhật \(ABCD\) có chiều dài \(AB = 10{\rm{\;cm}}\) và chiều rộng \(BC = 5{\rm{\;cm}}\); Người ta cắt bỏ miền \(\left( R \right)\) được giới hạn bởi cạnh \(CD\) của hình chữ nhật và hai nửa đường parabol có chung đỉnh là trung điểm của cạnh \(AB\), chúng lần lượt đi qua hai đầu mút \(C,D\) của hình chữ nhật đó (phần tô đậm như hình vẽ). Phần còn lại cho quay quanh trục \(AB\) để tạo nên một đồ vật làm trang trí, thể tích của vật trang trí đó bằng
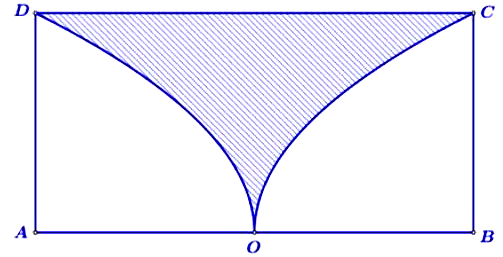
Đáp án đúng là: A
Đáp án cần chọn là: A
Cho tam giác ABC vuông tại A, có chu vi bằng 24. Khi đó
a) Độ dài cạnh huyền luôn lớn hơn
b) Độ dài cạnh góc vuông nhỏ hơn luôn nhỏ hơn
c) Nếu độ dài cạnh huyền lớn hơn độ dài 1 cạnh góc vuông là 2cm thì tam giác đó có diện tích bằng
Đáp án đúng là: \(\frac{{24}}{{\sqrt 2 + 1}}\); \(\frac{{24}}{{2 + \sqrt 2 }}\); 24
Đáp án cần chọn là: \(\frac{{24}}{{\sqrt 2 + 1}}\); \(\frac{{24}}{{2 + \sqrt 2 }}\); 24
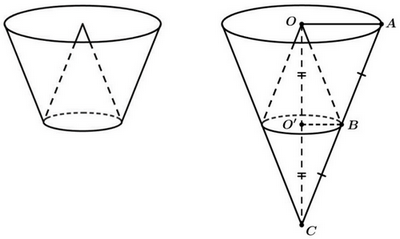
Một cái thùng đựng nước được tạo thành từ việc cắt mặt xung quanh của một hình nón bởi một mặt phẳng vuông góc với trục của hình nón. Miệng thùng là đường tròn có bán kính bằng hai lần bán kính mặt đáy của thùng. Bên trong thùng có một cái phễu dạng hình nón có đáy là đáy của thùng, có đỉnh là tâm của miệng thùng (xem hình minh họa). Biết rằng đổ 12 lít nước vào thùng thì đầy thùng (nước không chảy được vào bên trong phễu), tính thể tích của phễu.
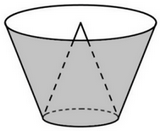
Đáp án đúng là: 2
Áp dụng công thức tính thể tích hình nón.
Đáp án cần điền là: 2
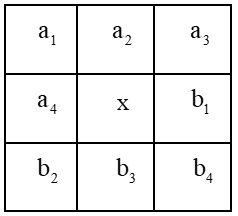
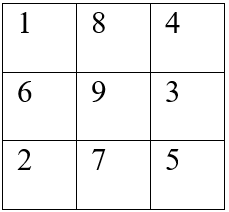
Cho bảng ô vuông \(3 \times 3\) (gồm ba dòng và ba cột). Người ta ghi tất cả các số thuộc tập hợp \(\left\{ {1;2;3;4;5;6;7;8;9} \right\}\) vào các ô vuông của bảng, mỗi ô vuông ghi một số, sao cho tổng các số trong mỗi bảng vuông con cỡ \(2{\rm{x}}2\) đều bằng nhau.
Ví dụ một cách ghi các số vào bảng thỏa mãn yêu cầu bài toán như hình sau có tổng các số trong mỗi bảng vuông con cỡ $2 \times 2$ đều bằng 18 như hình
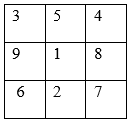
Hỏi trong tất cả các cách ghi các số vào bảng thỏa mãn yêu cầu bài toán, tìm giá trị lớn nhất của tổng các số trong mỗi bảng vuông con cỡ \(2 \times 2\).
Đáp án đúng là: 24
Đáp án cần điền là: 24
Phần 2: Tư duy đọc hiểu
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 1 đến 10:
Thuốc trừ sâu từ cỏ ngọt?
Phát hiện này xuất phát từ ý tưởng của nhà nghiên cứu Simon D. Kaschock-Marenda. Ông đã cho ruồi giấm ăn chất làm ngọt Truvia (do Tập đoàn Cargill sản xuất) và một số chất ngọt khác, rồi giữ chúng trong lọ cùng với ruồi giấm trưởng thành. Gần một tuần sau, ông thấy những con ruồi ăn chất làm ngọt Truvia đã chết, nhưng những con ruồi ăn các chất ngọt khác vẫn sống. Ban đầu ông nghĩ rằng đây có thể chỉ là một sự tình cờ, nhưng những lần thí nghiệm sau vẫn cho kết quả tương tự. Những con ruồi được nuôi bằng Truvia chỉ sống khoảng sáu ngày, còn những con ruồi ăn đường cát bình thường thì sống đến tuổi thọ bình thường, khoảng 40 - 50 ngày.
Truvia là chất làm ngọt tự nhiên, được chiết xuất từ cỏ ngọt Nam Mỹ, nên các nhà khoa học nghĩ rằng loại cỏ ngọt này có chứa các thành phần có khả năng tiêu diệt ruồi giấm.
Nhưng khi ruồi giấm ăn thức ăn có chứa Purevia - một chất làm ngọt khác cũng được chiết xuất từ cỏ ngọt, chúng không có phản ứng giống như khi ăn chất làm ngọt Truvia. Tuổi thọ của chúng vẫn không thay đổi.
Vì vậy, các nhà nghiên cứu tại Drexel đã sử dụng phương pháp sắc ký lỏng hiệu năng cao (HPLC) để phân tích Truvia. Kết quả cho thấy hơn 90% hàm lượng của Truvia là erytritol.
Erythritol là một chất làm ngọt “không calo”, được tìm thấy trong trái cây và thực phẩm lên men. Nó đóng vai trò như chất độn trong Truvia. Chiết xuất lá cỏ ngọt có vị ngọt gấp khoảng 200 lần đường, nên erythritol giúp tạo ra độ ngọt đồng đều trong toàn bộ sản phẩm được làm ngọt. Ngoài ra, erytritol đã được Cục quản lý Thực phẩm và Dược phẩm Mỹ (FDA) công nhận là an toàn và được chấp thuận làm phụ gia thực phẩm trên toàn cầu.
Để xác định xem liệu erytritol có phải là thủ phạm thực sự gây độc cho ruồi giấm hay không, nhóm nghiên cứu đã cho ruồi giấm vào trong các lọ chứa erythritol ở nồng độ cao hơn. Kết quả là, sau một hoặc hai ngày ăn thức ăn tẩm erythritol có nồng độ cao nhất (2M), tất cả các con ruồi đều chết.
Nhóm của Marenda đã nhận được bằng sáng chế tạm thời đối với việc sử dụng erythritol làm thuốc diệt ruồi giấm và một số côn trùng khác. Theo nhóm nghiên cứu, phương pháp mới này rất hứa hẹn vì khi cho ruồi giấm lựa chọn giữa erythritol và sucroza thì chúng ăn cả hai loại. Điều này có nghĩa là chúng ta có thể nhử mồi ngay cả khi côn trùng đang có thực phẩm khác.
Tuy nhiên, hợp chất mới còn phải trải qua một chặng đường dài trước khi có thể trở thành một loại thuốc trừ sâu. Các nhà nghiên cứu sẽ phải chứng minh rằng erythritol không độc hại đối với các loài côn trùng có ích như ong và nhiều động vật khác như chim.
Trả lời cho các câu 41, 42, 43, 44, 45, 46, 47, 48, 49, 50 dưới đây:
Ý chính của bài viết trên là gì?
Đáp án đúng là: B
Căn cứ bài đọc hiểu, phân tích.
Đáp án cần chọn là: B
Tuổi thọ trung bình của một con ruồi giấm là bao nhiêu?
Đáp án đúng là: D
Căn cứ bài đọc hiểu, phân tích.
Đáp án cần chọn là: D
Hàm lượng chính của chất Truvia là?
Đáp án đúng là: C
Căn cứ bài đọc hiểu, phân tích.
Đáp án cần chọn là: C
Phương pháp HPLC được nhắc đến trong đoạn 4 là:
Đáp án đúng là: D
Căn cứ bài đọc hiểu, phân tích.
Đáp án cần chọn là: D
Cụm từ “không calo” trong bài được hiểu là:
Đáp án đúng là: A
Căn cứ bài đọc hiểu, phân tích.
Đáp án cần chọn là: A
Từ thí nghiệm ở đoạn 6, chúng ta có thể kết luận được điều gì?
Đáp án đúng là: C
Căn cứ bài đọc hiểu, phân tích.
Đáp án cần chọn là: C
Cụm từ “phương pháp mới này” trong đoạn 7 dùng để chị phương pháp nào dưới đây:
Đáp án đúng là: B
Căn cứ bài đọc hiểu, phân tích.
Đáp án cần chọn là: B
Nhận định nào dưới đây KHÔNG đúng?
Đáp án đúng là: A
Căn cứ bài đọc hiểu, phân tích.
Đáp án cần chọn là: A
Điền từ còn thiếu để hoàn thành câu văn sau:
Chiết xuất lá cỏ ngọt có vị ngọt gấp khoảng 200 lần đường, nên erythritol giúp tạo ra độ ngọt ________ trong toàn bộ sản phẩm được làm ngọt.
Đáp án đúng là: A
Căn cứ bài đọc hiểu, phân tích.
Đáp án cần chọn là: A
Các nhà nghiên cứu phải chứng minh thêm điều gì trước khi Erythritol trở thành một loại thuốc trừ sâu?
Đáp án đúng là: A
Căn cứ bài đọc hiểu, phân tích.
Đáp án cần chọn là: A
Dựa vào thông tin dưới đây để trả lời các câu từ 1 đến 10
(1) Theo báo cáo của Hootsuite về thế giới số năm 2020, đến cuối năm 2020, lượng người dùng Internet trên toàn cầu đạt 4,66 tỷ trong đó 4,2 tỷ người đang sử dụng mạng xã hội ngoài ra có 5,22 tỷ người đang sử dụng điện thoại di động.
(2) Lượng người dùng điện thoại di động trên toàn cầu hiện nay tương đương 66,6% dân số thế giới. Dựa trên số liệu của Liên Hợp Quốc, dân số toàn cầu tính đến tháng 1/2021 là 7,83 tỷ, tốc độ tăng 1%/năm. Điều đó đồng nghĩa trong năm 2020, dân số toàn cầu đã tăng hơn 80 triệu người. Từ tháng 1/2020, lượng người dùng điện thoại di động trên thế giới đã tăng 1,8% (tương đương 93 triệu), trong khi tổng thiết bị kết nối di động (một người có thể sở hữu nhiều máy) tăng 0,9% lên mức 8,02 tỷ thiết bị.
(3) Lượng người dùng Internet trên toàn cầu tăng 7,3% (tương đương 316 triệu) so với cùng kỳ năm ngoái. Tỷ lệ sử dụng Internet hiện tại là 59,5%, tuy nhiên con số thực tế có thể cao hơn do dịch Covid-19 khiến nhu cầu sử dụng Internet tăng mạnh.
(4) Có khoảng 4,2 tỷ người sử dụng các dịch vụ mạng xã hội trên toàn cầu, tăng hơn 13% (490 triệu) chỉ trong 12 tháng, tương đương 53% dân số toàn cầu. Năm 2020, trung bình có 1,3 triệu người mới sử dụng mạng xã hội mỗi ngày. 2 giờ 25 phút mỗi ngày là thời gian bỏ ra trung bình trên mạng xã hội. Dự đoán trong năm 2021, người dùng sẽ dành tổng cộng 3,7 nghìn tỷ giờ trên các ứng dụng này. Philippines là quốc gia sử dụng mạng xã hội nhiều nhất, trung bình 4 giờ 15 phút mỗi ngày, nhiều hơn 30 phút so với quốc gia xếp thứ 2 là Colombia. Trong khi đó, người Nhật dành 51 phút mỗi ngày trên mạng xã hội.
(5) Dữ liệu của App Annie cho thấy người dùng Android trên toàn cầu sử dụng smartphone hơn 4 giờ/ngày, tương đương 3,5 nghìn tỷ giờ trong 12 tháng qua. Đối với người dùng Internet, họ bỏ ra trung bình 3 giờ 39 phút mỗi ngày trên smartphone, nhiều hơn 7% so với thời gian xem TV mỗi ngày (3 giờ 24 phút).
(6) Người dùng Internet dành trung bình gần 7 giờ mỗi ngày trên mọi thiết bị, tương đương hơn 48 giờ mỗi tuần. Giả sử thời gian ngủ trung bình là 7-8 giờ, chúng ta đang dành 42% thời gian thức cho các hoạt động trực tuyến. Dù smartphone chiếm 53% thời gian sử dụng Internet, những thiết bị khác vẫn đóng vai trò quan trọng. Có 90% người dùng Internet lên mạng bằng smartphone, nhưng 2/3 trong số họ vẫn sử dụng laptop hoặc máy tính để bàn.
(7) Người dùng Philippines dành thời gian trên Internet lâu nhất, trung bình gần 11 giờ mỗi ngày. Brazil, Colombia và Nam Phi cũng dành trung bình hơn 10 giờ trực tuyến mỗi ngày. Người dùng Nhật Bản dành thời gian trực tuyến ít nhất, chưa đến 4,5 giờ mỗi ngày. Đáng chú ý khi thời gian dùng Internet tại Trung Quốc tương đối thấp, trung bình 5 giờ 22 phút mỗi ngày, ít hơn 1,5 giờ so với mức trung bình toàn cầu là 6 giờ 54 phút.
(8) Công cụ tìm kiếm vẫn là điều không thể thiếu. 98% người phản hồi cho biết họ sử dụng công cụ tìm kiếm mỗi tháng, trong đó 45% sử dụng tìm kiếm giọng nói. Gần 1/3 người dùng Internet sử dụng các ứng dụng tìm kiếm hình ảnh như Pinterest Lens, Google Lens.
(9) Một xu hướng thú vị là tìm kiếm trên mạng xã hội. Khoảng 45% người dùng Internet cho biết đã chuyển sang mạng xã hội khi cần tìm sản phẩm, dịch vụ. Ở độ tuổi 16-64, gần 77% người dùng mua hàng trực tuyến mỗi tháng. Năm 2020, các sản phẩm thời trang và làm đẹp chiếm tỷ trọng lớn nhất trong doanh thu thương mại điện tử B2C (business-to-consumer) toàn cầu, đạt 665 tỷ USD.
(Theo Zing)
Trả lời cho các câu 51, 52, 53, 54, 55, 56, 57, 58, 59, 60 dưới đây:
Ý nào sau đây thể hiện rõ nhất nội dung chính của bài đọc trên?
Đáp án đúng là: B
Đọc kĩ văn bản
Đáp án cần chọn là: B
Theo đoạn 1 và 2, đến cuối năm 2020 số người sử dụng internet tương đương bao nhiêu phần trăm dân số thế giới?
Đáp án đúng là: B
Đọc kĩ văn bản
Đáp án cần chọn là: B
Theo đoạn 4, số người sử dụng mạng xã hội trong năm 2019 là:
Đáp án đúng là: C
Đọc kĩ văn bản
Đáp án cần chọn là: C
Theo đoạn 5, trong năm 2020, thế giới có trung bình khoảng bao nhiêu thiết bị Android?
Đáp án đúng là: D
Đọc kĩ văn bản
Đáp án cần chọn là: D
Theo đoạn 6, ), có khoảng bao nhiêu người trên thế giới đang sử dụng Internet thông qua điện thoại thông minh?
Đáp án đúng là: B
Đọc kĩ văn bản
Đáp án cần chọn là: B
Theo đoạn 7. tại quốc gia có thời lượng sử dụng mạng Internet thấp nhất, trung bình mỗi người mỗi ngày dành bao nhiêu thời gian trực tuyến?
Đáp án đúng là: A
Đọc kĩ văn bản
Đáp án cần chọn là: A
Theo đoạn 8, ước tính có bao nhiêu người trên thế giới sử dụng công cụ tìm kiếm giọng nói?
Đáp án đúng là: A
Đọc kĩ văn bản
Đáp án cần chọn là: A
Dựa vào đoạn 9, ta có thể đưa ra suy luận nào sau đây?
Đáp án đúng là: D
Đọc kĩ văn bản
Đáp án cần chọn là: D
Dựa trên thông tin trong bài, lượng người dùng mạng xã hội trên toàn cầu trong năm 2020 đã tăng thêm bao nhiêu phần trăm so với cùng kỳ năm trước?
Đáp án đúng là: C
Đọc kĩ văn bản
Đáp án cần chọn là: C
Dựa vào bài viết, nếu dân số toàn cầu tính đến tháng 1/2021 là 7,83 tỷ người và lượng người dùng điện thoại di động tương đương 66,6% dân số, thì có bao nhiêu người trên toàn cầu không sử dụng điện thoại di động?
Đáp án đúng là: A
Đọc kĩ văn bản
Đáp án cần chọn là: A
Phần 3: Tư duy khoa học/Giải quyết vấn đề
Đọc văn bản sau và trả lời các câu hỏi từ 8 đến 14
Tia UVA và tia UVB là các dạng năng lượng khác nhau được gọi là bức xạ cực tím (UV) thường thấy dưới dạng ánh sáng mặt trời.
Tia UVA có lượng năng lượng thấp hơn và bước sóng dài hơn tia UVB. Chúng có thể đi vào lớp giữa của da bạn được gọi là lớp hạ bì. Tia UVA tạo ra 95% bức xạ UV chiếu xuống trái đất. Chúng có vai trò trong việc hình thành một số loại ung thư da .
Tia UVB có năng lượng cao hơn một chút so với tia UVA. Chúng có bước sóng ngắn chỉ có thể tiếp cận lớp ngoài cùng của da bạn được gọi là lớp biểu bì. Tia UVB có liên quan đến tình trạng bỏng da. Chúng cũng có vai trò quan trọng trong việc hình thành ung thư da, đặc biệt là một dạng ung thư da nguy hiểm được gọi là u hắc tố ác tính.
Hai nhóm sinh viên bắt đầu kiểm tra khả năng chặn ánh sáng UVB của vật liệu bằng cách sử dụng máy tính và một cảm biến được thiết kế đặc biệt để phát hiện bức xạ UVB.
Nhóm 1: Các thành viên của Nhóm 1 đặt cảm biến dưới ánh nắng đầy đủ và che chắn cảm biến với nhiều loại kính râm được tuyên bố là có khả năng chống tia UVB. Việc đo lường chỉ số UVB được thực hiện trên cảm biến UVB cho từng sản phẩm và dữ liệu được được ghi trong Bảng 1:
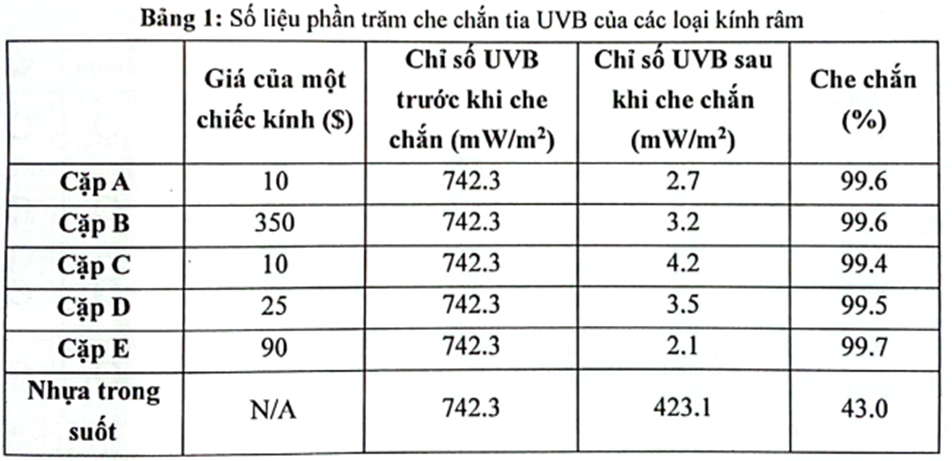
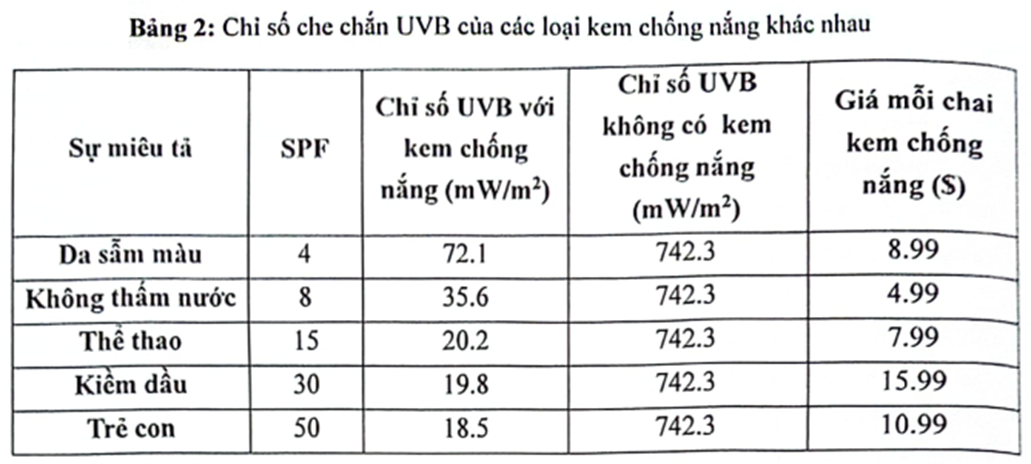
Nhóm 2: Các thành viên của Nhóm 2 đặt cảm biến dưới ánh nắng mặt trời và che chắn cảm biến đó bằng một mảnh thủy tinh. Họ đã thử nghiệm các loại kem chống nắng có chỉ số SPF tăng dần (chỉ số đo lường khả năng chống lại tia UV) trên kính và số liệu được ghi trong Bảng 2.
Trả lời cho các câu 61, 62, 63, 64, 65, 66, 67 dưới đây:
Dựa trên kết quả thí nghiệm của Nhóm 2, kết quả UVB có khả năng sẽ là bao nhiêu nếu thử nghiệm kem chống nắng SPF 60?
Đáp án đúng là: A
Sử dụng dữ kiện từ Bảng 2
Đáp án cần chọn là: A
Học sinh trong Nhóm 2 có thể cố gắng trả lời câu hỏi nào sau đây bằng cách sử dụng dữ liệu từ thí nghiệm của mình?
Đáp án đúng là: A
Sử dụng thông tin bài cung cấp và kết quả nghiên cứu của nhóm 2.
Đáp án cần chọn là: A
Câu nào sau đây CÓ NHIỀU khả năng đại diện cho biện pháp kiểm soát được sử dụng để đảm bảo độ tin cậy của dữ liệu trong thí nghiệm do Nhóm 2 thực hiện?
Đáp án đúng là: A
Sử dụng dữ kiện của Nhóm 2
Đáp án cần chọn là: A
Nhận xét nào sau đây biểu thị mối quan hệ đúng giữa SPF và khả năng chặn tia UVB?
Đáp án đúng là:
Sử dụng dữ kiện từ Bảng 2
Đáp án cần chọn là:
Chọn đúng/sai cho các nhận xét sau đây về kết quả của Nhóm 1:
| Đúng | Sai | |
|---|---|---|
| a) Có mối tương quan nghịch giữa giá cả và khả năng bảo vệ khỏi bức xạ UVB | ||
| b) Có mối tương quan tích cực giữa giá cả và khả năng bảo vệ khỏi bức xạ UVB | ||
| c) Không có mối tương quan nào giữa giá của một cặp kính râm và khả năng bảo vệ mắt khỏi bức xạ UVB của chúng | ||
| d) Kính râm không bảo vệ mắt khỏi bức xạ UVB. |
Đáp án đúng là: S; S; Đ; S
Dựa vào nghiên cứu của nhóm 1.
Đáp án cần chọn là: S; S; Đ; S
Giả sử kem chống nắng đang được thử nghiệm được mua trong chai 10 oz, loại kem chống nắng nào có chi phí tốt nhất về khả năng bảo vệ khỏi tia UVB (sử dụng công thức \(\$ /mW/m{{\rm{ }}^2}\) tia UVB bị chặn).
Đáp án đúng là: C
Sử dụng dữ iện từ bảng số liệu và công thức \(\$ /mW/m{{\rm{ }}^2}\) tia UVB bị chặn
Đáp án cần chọn là: C
Trong thí nghiệm của Nhóm 2, SPF là biến độc lập đang được thao tác và UVB là biến phụ thuộc đang được đo. Biểu đồ _______ thể hiện tốt nhất mối quan hệ giữa dữ liệu SPF và UVB từ thí nghiệm này?
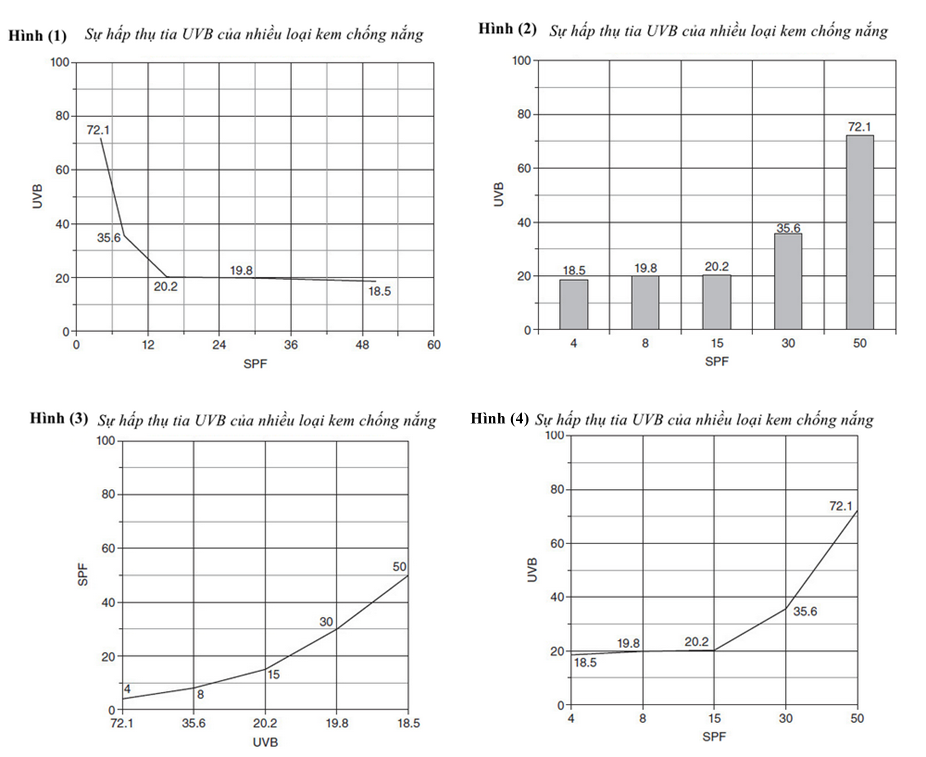
Đáp án đúng là: Hình (1)
Sử dụng dữ kiện từ bảng số liệu, đối chiếu với các biểu đồ đã cho
Đáp án cần điền là: Hình (1)
Đọc văn bản sau và trả lời các câu hỏi từ 1 đến 7
Một học sinh tiến hành khảo sát dao động
của một con lắc đơn. Các bước tiến hành như sau:
- Treo con lắc đơn vào một điểm cố định
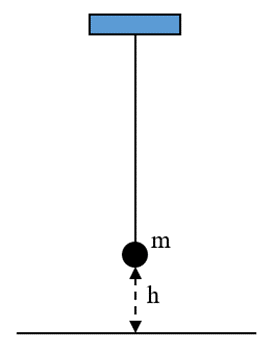
Hình 1
- Kích thích con lắc dao động và đo thời gian con lắc thực hiện được 10 dao động (t). Thay đổi các giá trị khác nhau của h, ghi lại thời gian con lắc thực hiện 10 dao động.
- Với mỗi giá trị của h, tiến hành đo 2 lần giá trị t. Kết quả thí nghiệm được cho bởi Bảng 1.
Chu kỳ là thời gian con lắc thực hiện một dao động, kí hiệu là T.
T và h liên hệ với nhau bởi công thức:\({T^2} = \dfrac{{4{\pi ^2}}}{g}\left( {k - h} \right)*\) với g là gia tốc rơi tự do và k là một hằng số.
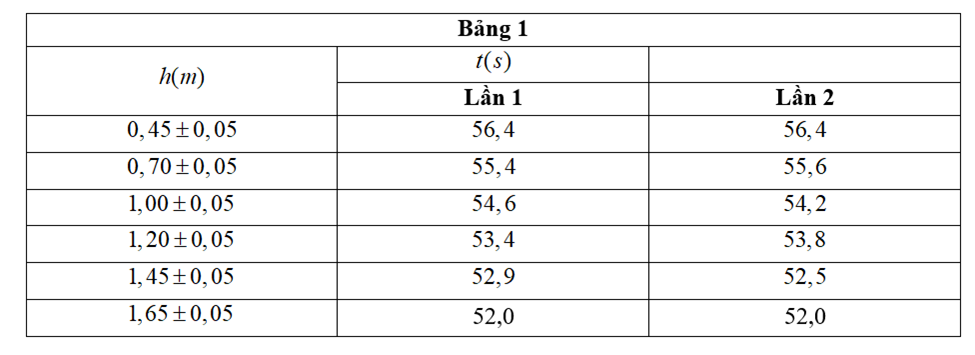
Trả lời cho các câu 68, 69, 70, 71, 72, 73, 74 dưới đây:
Cho các nhận xét sau đây, hãy cho biết đúng hay sai?
| Đúng | Sai | |
|---|---|---|
| a) Vì k là một hằng số nên khi sử dụng số liệu trong Bảng 1 và công thức (*) thì luôn được giá trị chính xác. | ||
| b) Khi thay đổi h tăng, chiều dài của dây giảm. Từ số liệu trong Bảng 1 và công thức (*) suy ra chu kỳ dao động của con lắc tỉ lệ thuận với chiều dài của nó. |
Đáp án đúng là: S; S
Sử dụng thông tin bài cung cấp
Đáp án cần chọn là: S; S
Từ bảng 1 ta thấy thời gian ngắn nhất để con lắc hiện hiện được 10 dao động là khi ở độ cao:
Đáp án đúng là: B
Phân tích số liệu từ bảng 1
Đáp án cần chọn là: B
Khi con lắc ở vị trí cân bằng, góc lệch của dây treo và phương thẳng đứng là \({60^0}\). Đúng hay sai?
| Đúng | Sai | |
|---|---|---|
| a) Đúng | ||
| b) Sai |
Đáp án đúng là: S; Đ
Vận dụng lí thuyết về con lắc đơn
Đáp án cần chọn là: S; Đ
Đồ thị hình nào sau đây thể hiện mối quan hệ giữa chu kì và chiều cao h?
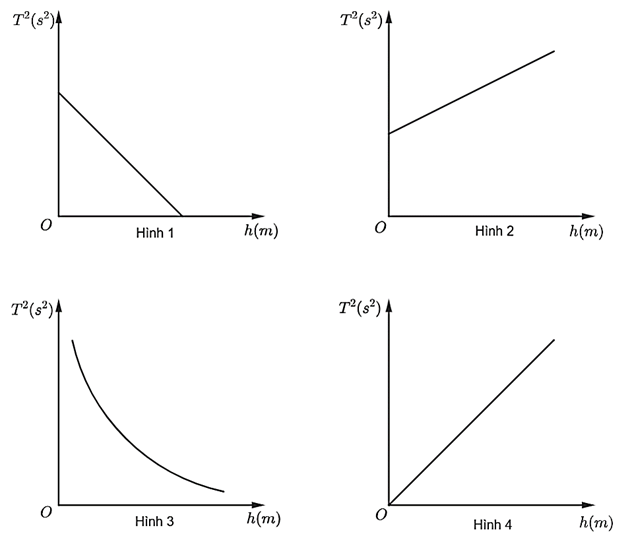
Đáp án đúng là: C
Dựa vào công thức đề cung cấp: \({T^2} = \dfrac{{4{\pi ^2}}}{g}\left( {k - h} \right)*\)
Đáp án cần chọn là: C
Chọn các nhận xét đúng cho các phát biểu sau đây?
Đáp án đúng là: A; B
Dựa vào công thức đề cung cấp: \({T^2} = \dfrac{{4{\pi ^2}}}{g}\left( {k - h} \right)*\)
Đáp án cần chọn là: A; B
Điền từ thích hợp vào chỗ trống:
Từ số liệu bảng 1 thì ta rút ra được khi độ cao h giảm thì chu kì dao động của con lắc sẽ _____
Đáp án đúng là: tăng
Phân tích số liệu từ bảng 1
Đáp án cần điền là: tăng
Khi chiều cao h của vật trong lần thử nghiệm tiếp theo là \(1,75 \pm 0,05\left( m \right)\) thì thời gian t (s) đo được sẽ có thể là:
Đáp án đúng là: B
Sử dụng số liệu bài cung cấp
Đáp án cần chọn là: B
Pepsin là một loại enzyme ở người có vai trò xúc tác quá trình tiêu hóa protein thành các đơn vị nhỏ hơn gọi là peptide. Pepsin ở dạng không hoạt động gọi là pepsinogen và có thể chuyển thành dạng hoạt động trong môi trường acid.
Thí nghiệm 1
Chuẩn bị 7 ống nghiệm khác nhau, đánh số từ 1 đến 7. Lần lượt thêm vào mỗi ống một lượng khác nhau các dung dịch casein, anserine và pepsin. Tiếp theo, pha loãng đến 10ml bằng dung dịch đệm, sao cho giá trị pH cuối cùng trong mỗi ống nghiệm đạt pH = 3. Mỗi ống được ủ ở một nhiệt độ khác nhau, không đổi trong 15 phút, sau đó được theo dõi để xác định hoạt động của enzyme pepsin. Tiến trình và kết quả thí nghiệm được thể hiện ở bảng 1.

Thí nghiệm 2
Chuẩn bị 7 ống nghiệm theo quy trình tương tự như ống nghiệm 3 của thí nghiệm 1. Đem các ống nghiệm này pha loãng với các dung dịch đệm khác nhau đến các độ pH khác nhau. Tiến trình và kết quả thí nghiệm được thể hiện ở bảng 2.
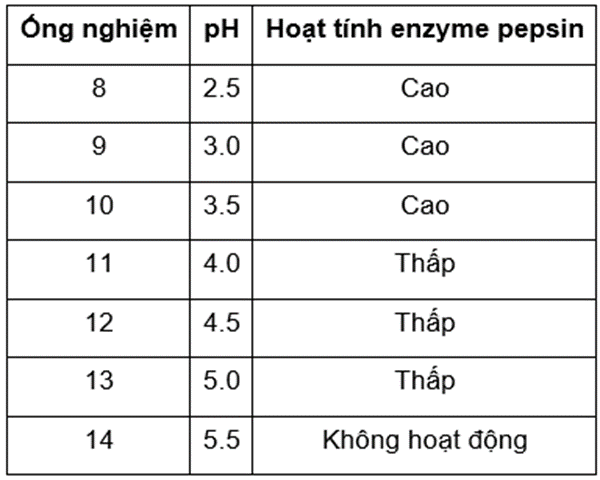
Trả lời cho các câu 75, 76, 77, 78, 79, 80 dưới đây:
Enzyme pepsin chỉ hoạt động trong môi trường có
Đáp án đúng là: B
Dựa vào dữ liệu đoạn văn.
Đáp án cần chọn là: B
Pepsin là enzyme tiêu hóa được tìm thấy ở
Đáp án đúng là: C
Dựa vào dữ liệu đoạn văn.
Đáp án cần chọn là: C
Giải thích tại sao các ống nghiệm 3 và 4, hoạt tính của enzyme pepsin cao, trong khi ống nghiệm 5 enzyme không có hoạt tính?
Đáp án đúng là: C
Phân tích số liệu, kết quả ở cả thí nghiệm 1.
Đáp án cần chọn là: C
Điền từ/cụm từ thích hợp vào chỗ trống?
Enzyme pepsin giúp phân giải các protein có trong thức ăn thành các đơn vị nhỏ hơn gọi là ________.
Đáp án đúng là: peptide
Dựa vào dữ liệu đoạn văn.
Đáp án cần điền là: peptide
Phát biểu dưới đây là đúng hay sai?
Pepsin có hoạt tính phân giải protein lớn nhất khi độ pH lớn hơn 4.0 và nhiệt độ khoảng 40°C.
Đáp án đúng là: B
Dựa vào dữ liệu thí nghiệm 1, 2.
Đáp án cần chọn là: B
Dạng enzyme chưa hoạt động (tiền enzyme) của pepsin là
Đáp án đúng là: pepsinogen
Dựa vào dữ liệu đoạn văn.
Đáp án cần chọn là: pepsinogen
Sắt (III) oxit (Fe2O3) thường được biết đến là gỉ sét. Fe2O3 được tạo ra do phản ứng của sắt – một kim loại rất phổ biến – với nước, H2O: 2Fe + 3H2O → Fe2O3 + 3H2.
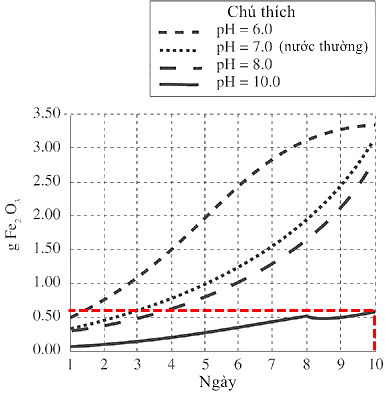
Bảng 1 cho biết lượng Fe2O3 được tạo ra theo thời gian từ 15 gam Fe ngâm trong các chất lỏng khác nhau: 100 mL nước cất. dung dịch muối được tạo ra từ việc hoà tan 20g muối trong 100 mL nước cất và dung dịch đường được tạo ra từ việc hoà tan 20 g đường trong 100 mL nước cất.
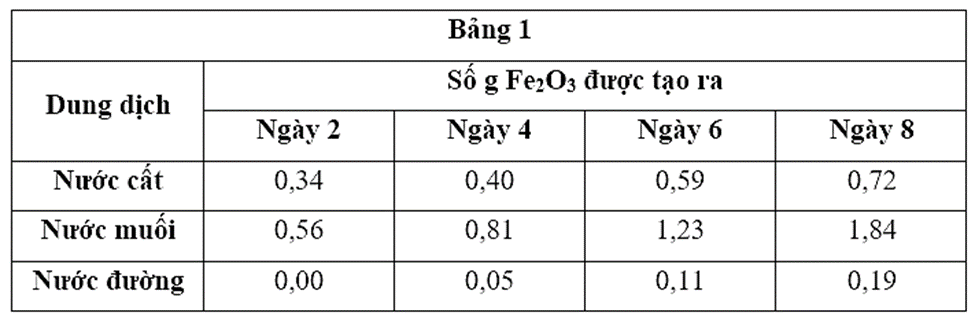
Thử nghiệm trên với nước cất được lặp lại 4 lần. Với mỗi thử nghiệm, 100 mL nước lại được đặt trong một pH khác nhau được tạo ra bởi dung dịch đệm.
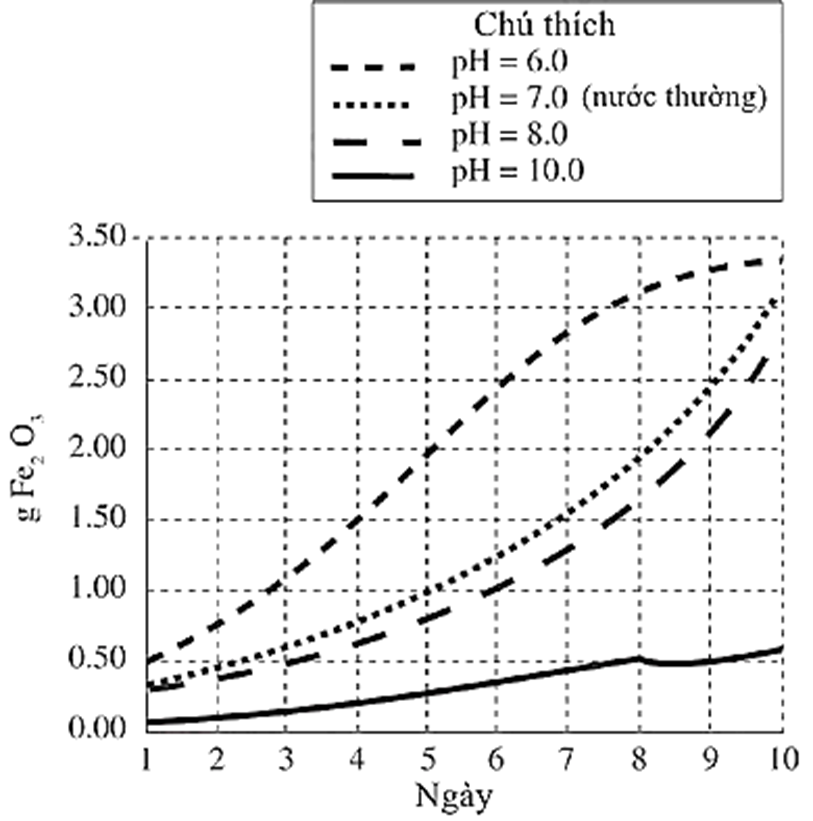
Trả lời cho các câu 81, 82, 83, 84, 85, 86, 87 dưới đây:
Dựa vào bảng 1, nếu đo lượng Fe2O3 được tạo ra trong ngày thứ 9 ở trong dung dịch nước muối thì giá trị thu được có thể là
Đáp án đúng là: D
Dựa vào số liệu bảng 1, nhận thấy khối lượng Fe2O3 được tạo ra trong môi các môi trường tăng lên theo thời gian. Vậy khối lượng Fe2O3 được tạo ra trong dung dịch nước muối của ngày thứ 9 sẽ phải nhiều hơn ngày thứ 8.
Đáp án cần chọn là: D
Thí nghiệm được thể hiện ở trong hình 1 và bảng 1, bằng cách đo tốc độ hình thành Fe2O3 mỗi ngày, những người thực hiện thí nghiệm cũng có thể đo được tốc độ của
Đáp án đúng là: A
Dựa vào phương trình hoá học và điều kiện môi trường của phản ứng xảy ra.
Đáp án cần chọn là: A
Dựa vào bảng 1, số gam Fe2O3 được tạo ra bởi dung dịch nước đường tính từ ngày 6 đến ngày 8 là ______.
Đáp án đúng là: 0,08
Dựa vào bảng 1, tìm lượng gỉ sắt được tạo ra ở ngày 6 và ngày 8 trong dung dịch nước đường.
Đáp án cần điền là: 0,08
Xem xét lượng Fe2O3 được tạo ra bởi dung dịch muối trong ngày 2. Dựa vào bảng 1 và hình 1, tại nước có đệm pH = 10 sẽ tạo ra một lượng Fe2O3 tương ứng như trên vào ngày thứ bao nhiêu?
Đáp án đúng là: D
Tìm khối lượng Fe2O3 được tạo ra bởi dung dịch muối trong ngày thứ 2. Trong hình 1, ứng với đường biểu diễn pH = 10 và khối lượng gỉ sắt được tạo ra.
Đáp án cần chọn là: D
Dựa vào bảng 1, đồ thị nào thể hiện tốt nhất lượng Fe2O3 được tạo ra trong dung dịch nước đường theo thời gian?
Đáp án đúng là: A
Quan sát bảng 1 để rút ra sự thay đổi lượng Fe2O3 giữa các ngày để từ đó chọn được đồ thị phù hợp.
Đáp án cần chọn là: A
Trong dung dịch nước thì tốc độ tạo thành gỉ sét là lớn nhất.
Đáp án đúng là: muối
Nhìn vào bảng 1 để so sánh khối lượng gỉ sét được tạo ra trong ba dung dịch. Ở dung dịch nào tạo ra được khối lượng Fe2O3 nhiều nhất thì dung dịch đó tạo gỉ sét tốt nhất.
Đáp án cần chọn là: muối
Mỗi phát biểu sau là đúng hay sai?
| Đúng | Sai | |
|---|---|---|
| a) pH càng lớn thì quá trình tạo thành gỉ sét càng tốt. | ||
| b) Trong đời sống và sản xuất người ta mong muốn đẩy mạnh quá trình tạo thành gỉ sét. | ||
| c) Quá trình tạo thành gỉ sét thực chất là phản ứng oxi hoá - khử. | ||
| d) Nếu thực hiện thí nghiệm trên với dung dịch bao gồm 20 mL rượu nguyên chẩt pha với 100 mL nước thì quá trình tạo thành gỉ sét sẽ là nhanh nhất. |
Đáp án đúng là: S; S; Đ; S
Dựa vào đồ thị trong hình 1 và kiến thức thực tế.
Đáp án cần chọn là: S; S; Đ; S
Đọc văn bản và trả lời các câu hỏi tiếp theo.
Bài báo về “Phổ đột biến gene gây bệnh ung thư di truyền ở người Việt Nam” trên ấn phẩm Frontiers in Oncology
Ung thư di truyền chiếm 5-10% các trường hợp ung thư và việc thực hiện xét nghiệm gene để đánh giá nguy cơ bị ung thư di truyền đã trở nên phổ biến và thường quy ở các nước phương Tây từ nhiều năm nay. Tuy nhiên, tại Việt Nam, xét nghiệm gene để xác định các đột biến gây bệnh chưa được thực sự chú trọng và đưa vào quy trình xét nghiệm thường quy. Vào năm 2020, nhóm tác giả, dẫn đầu là các chuyên gia đến từ Viện Di truyền Y học – Gene Solutions đã thực hiện nghiên cứu nhằm khám phá các đột biến gây ung thư di truyền ở người Việt Nam. Đây được đánh giá là nghiên cứu đầu tiên và lớn nhất về việc khám phá tần suất cũng như phổ đột biến ung thư di truyền ở Việt Nam.
Nghiên cứu đã được thực hiện trên 1.165 người Việt Nam đã làm xét nghiệm gene khảo sát 17 đột biến gene liên quan đến 11 loại ung thư di truyền phổ biến nhất trong năm 2020 tại Viện Di truyền Y học – Gene Solutions. Sử dụng công nghệ giải trình tự gene thế hệ mới (NGS), nhóm tác giả đã phân tích các đột biến trên 17 gene gây ung thư di truyền. Kết quả cho thấy một “bức tranh toàn diện” về phổ đột biến ung thư di truyền ở người Việt Nam và có đến 3.2% người tham gia có mang đột biến ung thư di truyền. Cụ thể, ở những người có tiền căn gia đình hoặc bản thân mắc ung thư (được đánh giá là nhóm nguy cơ cao cần đi thực hiện xét nghiệm gene của Viện Di truyền Y học – Gene Solutions và các hiệp hội ung thư) thì tỷ lệ này lên đến 4.2%, ở nhóm người không có tiền căn ung thư thì tỷ lệ mang đột biến ung thư di truyền là 2.6% (tức cứ 100 người sẽ có khoảng 3 người có mang đột biến ung thư di truyền).
Trần Văn Thuần và cộng sự, ấn phẩm Frontiers in Oncology.
Trả lời cho các câu 88, 89, 90, 91, 92, 93, 94 dưới đây:
Theo bài báo, công nghệ nào được nhóm tác giả sử dụng để phân tích đột biến gene gây ung thư di truyền?
Đáp án đúng là: B
Đọc kỹ bài báo để xác định công nghệ mà nhóm tác giả sử dụng.
Trong bài báo, đoạn nói về phương pháp nghiên cứu nêu rõ công nghệ được sử dụng là "giải trình tự gene thế hệ mới (NGS)".
Đáp án cần chọn là: B
Nếu một nhóm 1.000 người không có tiền căn ung thư tham gia xét nghiệm gene, theo tỷ lệ nghiên cứu, khoảng bao nhiêu người sẽ mang đột biến ung thư di truyền?
Đáp án đúng là: B
Tỷ lệ mang đột biến gene ung thư di truyền ở nhóm không có tiền căn ung thư là 2,6% (theo bài báo).
Đáp án cần chọn là: B
Tại sao việc thực hiện xét nghiệm gene để phát hiện đột biến ung thư di truyền ở Việt Nam chưa trở thành thường quy?
Đáp án đúng là: C
Đọc kỹ phần đầu bài báo. Phần này nêu rõ lý do việc xét nghiệm gene ở Việt Nam chưa phổ biến là vì chưa được chú trọng và chưa đưa vào quy trình xét nghiệm thường quy.
Đáp án cần chọn là: C
Tại sao tỷ lệ mang đột biến gene ung thư di truyền ở nhóm nguy cơ cao lại cao hơn so với nhóm không có tiền căn ung thư?
Đáp án đúng là: B
Đọc kỹ bài báo, thông tin nhóm nguy cơ cao được định nghĩa là những người có tiền căn gia đình hoặc bản thân mắc ung thư.
Đáp án đúng phải phù hợp với lý do liên quan đến di truyền.
Đáp án cần chọn là: B
Phát biểu: "Tỷ lệ mang đột biến gene ung thư di truyền ở nhóm người có tiền căn gia đình hoặc bản thân mắc ung thư cao hơn 1.6 lần so với nhóm không có tiền căn ung thư." Phát hiểu này là:
Đáp án đúng là: A
Đọc kỹ phần đầu bài báo.
Đáp án cần chọn là: A
Kéo các cụm từ thích hợp vào ô trống trong câu sau:
"Công nghệ được sử dụng trong nghiên cứu đã giúp phân tích phổ đột biến trên gene liên quan đến 11 loại ung thư di truyền phổ biến nhất."
Đáp án đúng là: 17; giải trình tự gene thế hệ mới (NGS)
Tìm các thông tin về công nghệ và số lượng gene trong bài báo.
Điền từ phù hợp vào các chỗ trống:
- Công nghệ sử dụng là "giải trình tự gene thế hệ mới (NGS)".
- Số lượng gene khảo sát là "17".
Đáp án cần chọn là: 17; giải trình tự gene thế hệ mới (NGS)
Xác định đúng/sai cho các phát biểu sau:
| Đúng | Sai | |
|---|---|---|
| a) Ung thư di truyền chiếm phần lớn số ca ung thư ở người. |
||
| b) Nghiên cứu khảo sát trên 1.165 người Việt Nam sử dụng công nghệ NGS. |
||
| c) Ở nhóm nguy cơ cao, tỷ lệ mang đột biến ung thư di truyền là 4.2%. |
||
| d) Kết quả nghiên cứu cho thấy tỷ lệ người Việt Nam mang đột biến ung thư di truyền thấp hơn 1%. |
Đáp án đúng là: S; Đ; Đ; S
Đọc kỹ nội dung của bài báo.
Đáp án cần chọn là: S; Đ; Đ; S
Hệ nhóm máu A, AB, B và O ở người do một gene trên nhiễm sắc thể thường có 3 allele là IA, IB và IO quy định; kiểu gene IA IA, IAIO quy định nhóm máu A; kiểu gene IBIB, IBIO quy định nhóm máu B; kiểu gene IAIB quy định nhóm máu AB; kiểu gene IOIO quy định nhóm máu O.
M. A. Khan (2014) và các nghiên cứu khác đã công bố rằng tần số các allele IA, IB, IO và tỉ lệ các kiểu gene về locus này trong các cộng đồng người Kinh ở Việt Nam tuân theo định luật Hardy – Weinberg, các khác biệt không có ý nghĩa thống kê. Tỉ lệ % từng nhóm máu được trình bày ở bảng sau:

Trả lời cho các câu 95, 96, 97, 98, 99, 100 dưới đây:
Cho phát biểu sau: “Tất cả những người có nhóm máu O đều không có allele IA và IB”. Phát biểu này là:
Đáp án đúng là: A
Dựa vào dữ liệu đề bài.
Đáp án cần chọn là: A
Phát biểu: "Trong một cộng đồng người Kinh, xác suất ngẫu nhiên để một người thuộc nhóm máu AB thấp hơn 5 lần so với nhóm máu B."
Đáp án đúng là: B
So sánh tỉ lệ nhóm máu AB và nhóm máu B:
+ Nhóm máu AB: 5,76%
+ Nhóm máu B: 27%
Đáp án cần chọn là: B
Một cặp vợ chồng người Kinh thuộc nhóm máu AB và nhóm máu O có thể sinh con thuộc nhóm máu nào sau đây?
Đáp án đúng là: A
Xác định kiểu gene của cha mẹ:
Nhóm máu AB: kiểu gene IAIB
Nhóm máu O: kiểu gene IOIO
Sơ đồ lai:
P: IAIB × IOIO → F: 50% IAIo : 50% IBIO
Đáp án cần chọn là: A
Trong một cộng đồng gồm 1.000 người, dựa vào tỉ lệ trong bảng, ước tính số người có nhóm máu A.
Đáp án đúng là: A
Sử dụng tỉ lệ phần trăm nhóm máu A (23,68%)
Đáp án cần chọn là: A
Xác định đúng/sai cho các phát biểu sau:
| Đúng | Sai | |
|---|---|---|
| a) Nhóm máu O có tỉ lệ thấp nhất trong cộng đồng người Kinh. |
||
| b) Tỉ lệ nhóm máu AB là nhỏ nhất trong bảng tỉ lệ. |
||
| c) Nhóm máu B chiếm tỉ lệ cao hơn nhóm máu A. |
||
| d) Các tỉ lệ nhóm máu trong bảng tuân theo định luật Hardy – Weinberg. |
Đáp án đúng là: S; Đ; Đ; Đ
Phân tích bài đọc.
Đáp án cần chọn là: S; Đ; Đ; Đ
Nhóm máu AB có bao nhiêu kiểu gene cùng quy định?
Đáp án đúng là: 1
Hệ nhóm máu A, AB, B và O ở người do một gene trên nhiễm sắc thể thường có 3 allele là IA, IB và IO quy định; kiểu gene IA IA, IAIO quy định nhóm máu A; kiểu gene IBIB, IBIO quy định nhóm máu B; kiểu gene IAIB quy định nhóm máu AB; kiểu gene IOIO quy định nhóm máu O.
Đáp án cần điền là: 1