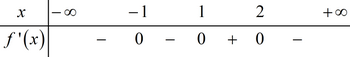Phần 1: Toán học và xử lý số liệu
Tính đạo hàm của hàm số \(y = {\log _2}\left( {3x} \right)\).
Đáp án đúng là: C
Đạo hàm của hàm số \(f\left( x \right) = {\log _a}\left( {u\left( x \right)} \right),\,\,a > 0\) là \(f'\left( x \right) = \dfrac{{u'\left( x \right)}}{{u\left( x \right).\ln a}}\).
Đáp án cần chọn là: C
Đồ thị hàm số nào sau đây có đúng 1 đường tiệm cận ngang?
Đáp án đúng là: C
Đường thẳng \(y = {y_0}\) là TCN của đồ thị hàm số nếu thỏa mãn một trong các điều kiện sau: \(\mathop {\lim }\limits_{x \to + \infty } y = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } y = {y_0}\).
Đáp án cần chọn là: C
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ dưới đây:
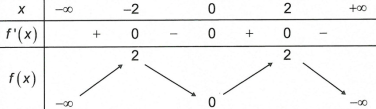
Mệnh đề nào dưới đây sai?
Đáp án đúng là: A
Quan sát BBT.
Đáp án cần chọn là: A
Cho hàm số \(y = \dfrac{{x + m}}{{x - 1}}\) (với m là tham số thực) thỏa mãn \(\mathop {\min }\limits_{\left[ {2;4} \right]} y = 3\). Mệnh đề nào dưới đây là đúng?
Đáp án đúng là: C
- Tính y’.
- Xét các TH hàm số đồng biến, nghịch biến trên [2;4], từ đó suy ra \(\mathop {\min }\limits_{\left[ {2;4} \right]} y\).
- Giải phương trình \(\mathop {\min }\limits_{\left[ {2;4} \right]} y = 3\) tìm m trong mỗi TH.
Đáp án cần chọn là: C
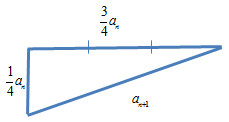
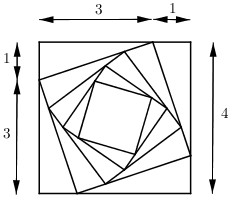
Cho hình vuông \({C_1}\) có độ dài cạnh bằng 4. Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để được hình vuông \({C_2}\)( tham khảo hình vẽ). Từ hình vuông \({C_2}\) tiếp tục làm như vậy để được hình vuông \({C_3}\),... . Tiếp tục quá trình trên ta được dãy các hình vuông \({C_1},{C_2},{C_3},...,{C_n}...\). Gọi \({S_1},{S_2},{S_3},...,{S_n}...\)tương ứng là diện tích các hình vuông \({C_1},{C_2},{C_3},...,{C_n}...\). Tính tổng \({S_1} + {S_2} + {S_3} + ... + {S_n} + ...\) (nhập kết quả dưới dạng phân số a/b)
Đáp án đúng là: 128/3
Sử dụng công thức tính tổng của cấp số nhân lùi vô hạn \({S_n} = \dfrac{{{u_1}}}{{1 - q}}\) với \({u_1}\) là số hạng đầu tiên, \(q\) là công bội của cấp số nhân.
Đáp án cần điền là: 128/3
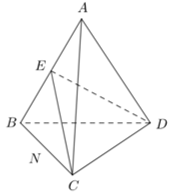
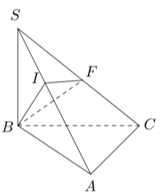
Cho tứ diện \(ABCD\) có hai mặt \(ABC\) và \(ABD\) là các tam giác đều. Góc giữa \(AB\) và \(CD\) có số đo bằng
Đáp án đúng là: C
Gọi \(E\) là trung điểm của \(AB\).
Chứng minh \(\left( {AB,CD} \right) = {90^0}\).
Đáp án cần chọn là: C
Khi thống kê chỉ số đường huyết (đơn vị: $\text{mmol}/\text{l}$) của 28 người cao tuổi trong một lần đo, ta được kết quả sau:

Ghép nhóm cho mẫu số liệu trên thành tám nhóm có độ dài bằng nhau trong đó có một nhóm là $\left\lbrack {7,4;7,6} \right)$. Tính số trung bình của mẫu số liệu ghép nhóm trên? (kết quả làm tròn đến hàng phần mười)
Đáp án đúng là: 7,4
Ghép nhóm mẫu số liệu tìm tần số từ đó tìm số trung bình
Số trung bình của mẫu số liệu ghép nhóm kí hiệu là $\overline{x} = \dfrac{m_{1}x_{1} + \ldots + m_{k}x_{k}}{n}$
Đáp án cần điền là: 7,4
Cho \(\int\limits_1^2 {\left[ {3f\left( x \right) - 2x} \right]dx = 6} \). Khi đó \(\int\limits_1^2 {f\left( x \right)dx} \) bằng
Đáp án đúng là: D
\(\int\limits_a^b {\left[ {m.f\left( x \right) \pm n.g\left( x \right)} \right]dx} = m\int\limits_a^b {f\left( x \right)dx} \pm n\int\limits_a^b {g\left( x \right)dx} \,\,\left( {m,n \in {\bf{R}}} \right)\).
Đáp án cần chọn là: D
Sản lượng lúa (tạ) của 40 thửa ruộng thí nghiệm có cùng diện tích được trình bày trong bảng phân bố tần số sau đây:

Tìm n biết sản lượng trung bình của 40 thửa ruộng là 22,1 tạ.
Đáp án đúng là: B
Công thức trung bình $\overline{x} = \dfrac{x_{1}m_{1} + x_{2}m_{2} + .... + x_{n}.m_{n}}{m_{1} + m_{2} + ... + m_{n}}$
Đáp án cần chọn là: B
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
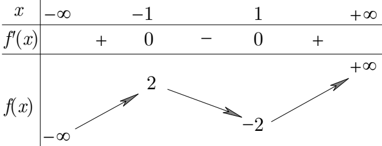
Số nghiệm thực phân biệt của phương trình \(f'\left( {f\left( x \right) + 3} \right) = 0\) là
Đáp án đúng là: B
Sử dụng tương giao đồ thị.
Đáp án cần chọn là: B
Theo dõi thời tiết hai huyện kề nhau A và B người ta nhận thấy trong cùng một ngày, nếu huyện B không mưa thì khả năng huyện A không mưa là $65 \%$, còn nếu huyện A không mưa thì khả năng huyện B không mưa là $60 \%$. Hơn nữa, xác suất cả hai huyện A và B có mưa trong cùng một ngày là $10 \%$. Hãy tính xác suất để ít nhất một trong hai huyện có mưa trong một ngày (làm tròn kết quả dưới dạng phân số a/b).
Đáp án đúng là: 509/860
Gọi $A$ và $B$ lần lượt là biến cố huyện A và B có mưa trong một ngày.
Đặt $a=P(A)$ và $b=P(B)$ với $a, b \in[0 ; 1]$.
Lập hệ phương trình tìm a, b từ đó tính $P(A \cup B)$
Đáp án cần điền là: 509/860
Một công ty thực hiện trả lương cho các kĩ sư theo phương thức sau: Mức lương của quý làm việc đầu tiên cho công ty là 15 triệu đồng/quý và kể từ quý làm việc thứ hai mức lương sẽ được tăng thêm 1,5 triệu đồng mỗi quý. Tổng số tiền lương một kĩ sư được nhận sau 3 năm làm việc cho công ty là:
Đáp án đúng là: B
Tính số lương của từng quý, sau đó tính tổng lương sau 3 năm = 12 quý.
Sử dụng công thức: \(1 + 2 + 3 + ... + n = \dfrac{{n\left( {n + 1} \right)}}{2}\).
Đáp án cần chọn là: B
Trong không gian \(Oxyz\), đường thẳng \(d\) đi qua 2 điểm \(A\left( {2; - 1;8} \right)\) và \(B\left( {3;2;3} \right)\) có phương trình là
Đáp án đúng là: C
Phương trình chính tắc của đường thẳng đi qua \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có 1 VTCP \(\overrightarrow u \left( {a;b;c} \right),\,\,\left( {a,b,c \ne 0} \right)\) là: \(\dfrac{{x - {x_0}}}{a} = \dfrac{{y - {y_0}}}{b} = \dfrac{{z - {z_0}}}{c}\).
Đáp án cần chọn là: C
Cho \(A\) và \(B\) là hai biến cố độc lập với nhau. Biết \(P\left( A \right) = 0,3;P\left( B \right) = 0,7\). Tính xác suất của biến cố \(AB\) ?
Đáp án đúng là: B
Công thức nhân xác suất
Đáp án cần chọn là: B
Trong lớp chuyên Toán có 36 bàn học cá nhân (mỗi bàn chỉ được xếp nhiều nhất một bạn), được xếp thành 4 hàng và 9 cột (các hàng được đánh số từ trên xuống dưới theo thứ tự từ 1 đến 4 , các cột được đánh số từ trái qua phải theo thứ tự từ 1 đến 9). Biết sĩ số học sinh của lớp là 35. Sau học kì I, thầy chủ nhiệm xếp lại chỗ ngồi cho các bạn học sinh trong lớp. Giả sử trước thời điểm chuyển chỗ bạn ngồi ở hàng thứ $m$, cột thứ $n$ và sau khi chuyển chỗ bạn đó sẽ ngồi ở hàng thứ $a_{m}$, cột thứ $a_{n}$ thì ta gán cho bạn đó số nguyên là $\left( {a_{m} + a_{n}} \right) - \left( {m + n} \right)$. Nếu ban đầu bàn trống ở vị trí $\left( {1;1} \right)$, sau khi chuyển chỗ bàn trống ở vị trí $\left( {2;5} \right)$ thì tổng của 35 số nguyên được gán cho 35 bạn là bao nhiêu?
Đáp án đúng là: -5
Suy luận logic
Đáp án cần điền là: -5
Trong mặt phẳng với hệ toạ độ Oxy, cho hai điểm A(1;1), B(-2;4) và đường thẳng \(\Delta :\,\,mx - y + 3 = 0.\) Tìm tất cả các giá trị của tham số m để \(\Delta \) cách đều hai điểm A, B.
Đáp án đúng là: C
\(\Delta \) cách đều A, B khi và chỉ khi \(\left[ \begin{array}{l}I \in \Delta \\\Delta //AB\end{array} \right.\).
Đáp án cần chọn là: C
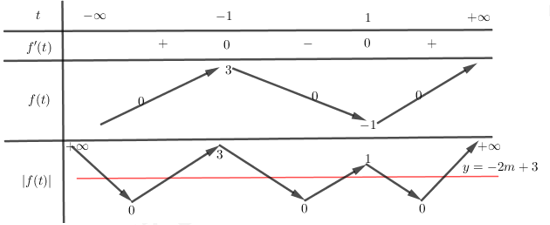
Cho hàm số \(y = f\left( x \right)\) liên tục trên \({\bf{R}}\) và có đồ thị như hình vẽ dưới đây
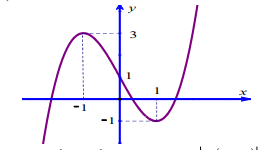
Tập hợp tất cả các giá trị của tham số \(m\) để phương trình \(\left| {f\left( {\cos x} \right)} \right| = - 2m + 3\) có 4 nghiệm thuộc khoảng \(\left[ {0;2\pi } \right]\) là
Đáp án đúng là: D
Phương trình \(\left| {f\left( {\cos x} \right)} \right| = - 2m + 3\) có 4 nghiệm thuộc khoảng \(\left[ {0;2\pi } \right]\) \( \Leftrightarrow \)Phương trình \(\left| {f\left( t \right)} \right| = - 2m + 3\) có 2 nghiệm phân biệt thuộc khoảng \(\left( { - 1,1} \right]\).
Từ đồ thị hàm số \(y = f\left( x \right)\), lập BBT của hàm số \(y = \left| {f\left( t \right)} \right|\).
Dựa vào BBT \(y = \left| {f\left( t \right)} \right|\) đánh giá giá trị của \(m\).
Đáp án cần chọn là: D
Gọi $S$ là phần hình phẳng màu xanh được tạo bởi hai đồ thị hàm số $y = \sin x + 1$ và $y = \cos x + 1$ như hình vẽ dưới. Biết thể tích của vật thể được tạo thành khi quay $S$ quanh trục Ox là $V = a\sqrt{b}\pi + c\pi^{2}\,$, với $a,b,c \in {\mathbb{N}}$, $b$ là số nguyên tố. Tính giá trị của biểu thức $P = a + b + c$. (nhập đáp án vào ô trống)
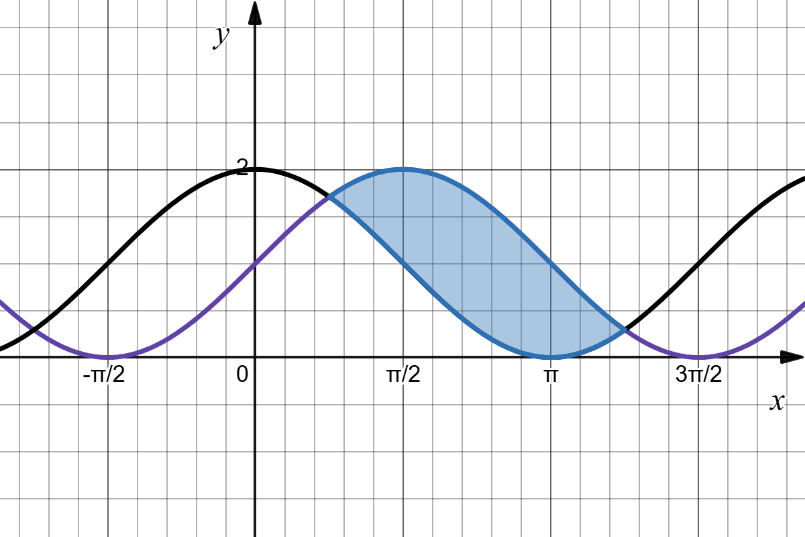
Đáp án đúng là: 6
Áp dụng công thức tính thể tích khối tròn xoay.
Đáp án cần điền là: 6
Nếu hai biến cố $A,B$ thỏa mãn $P(A) = 0,3,P(B) = 0,6$ và $P\left( {A \mid B} \right) = 0,4$ thì $P\left( {B \mid A} \right)$ bằng
Đáp án đúng là: A
Công thức xác suất $P\left( B \middle| A \right) = \dfrac{P(B).P\left( A \middle| B \right)}{P(A)}$
Đáp án cần chọn là: A
Đề thi kiểm tra 15 phút có 10 câu trắc nghiệm, mỗi câu có 4 phương án trả lời, trong đó có một phương án đúng, trả lời đúng mỗi câu được 1,0 điểm. Mỗi thí sinh làm cả 10 câu, mỗi câu chọn một phương án. Tính xác suất để thí sinh đó đạt từ 8,0 điểm trở lên.
Đáp án đúng là: A
Xác suất để chọn đáp án đúng là \(\dfrac{1}{4}\), xác suất chọn đáp án sai là \(\dfrac{3}{4}\).
Đáp án cần chọn là: A
Hai bạn An và Bình cùng tham gia chạy điền kinh ở Hội khỏe Phù Đổng cấp Tỉnh. An tham gia chạy cự ly 100 mét, Bình tham gia chạy cự ly 200 mét. Xác suất đạt huy chương vàng của An và Bình lần lượt là 0,6 và 0,7 . Tính xác suất để hai bạn tham gia có đúng một bạn đạt huy chương vàng.
Đáp án đúng là: 0,46
Gọi \(A\) : "An đạt huy chương vàng"; \(B\) :"Bình đạt huy chương vàng";
\(C\) : "Hai bạn tham gia có đúng một bạn đạt huy chương vàng".
Khi đó: \(C = A.\bar B \cup \bar A.B\)
Đáp án cần điền là: 0,46
Khoảng tứ phân vị của mẫu số liệu 2 ; 3 ; 4 ; 5 ; 6 là
Đáp án đúng là: A
Khoảng tứ phân vị ($\Delta_{Q}$) là hiệu giữa tứ phân vị thứ ba ($Q_{3}$) và tứ phân vị thứ nhất ($Q_{1}$).
$\Delta_{Q} = Q_{3} - Q_{1}$.
Để tìm $Q_{1}$ và $Q_{3}$, ta sắp xếp mẫu số liệu theo thứ tự tăng dần, sau đó tìm trung vị $Q_2$, rồi tìm trung vị của nửa dưới mẫu số liệu $Q_1$ và trung vị của nửa trên mẫu số liệu $Q_3$.
Đáp án cần chọn là: A
Đồ thị hàm số \(y = m{x^2} + \left( {2 - 3m} \right)x + 2m - 1\) luôn đi qua hai điểm cố định A, B với mọi m. Độ dài đoạn thẳng AB là:
Đáp án đúng là: B
- Đưa hàm số về dạng phương trình bậc nhất ẩn m: Xm + Y = 0.
- Tìm điều kiện để phương trình nghiệm đúng với mọi m: X = Y = 0.
- Suy ra tọa độ điểm A, B.
- Tính \(AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} \).
Đáp án cần chọn là: B
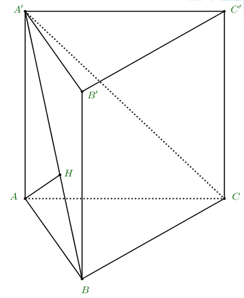
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có độ dài cạnh bên bằng 3, đáy \(ABC\) là tam giác vuông tại \(B\) và \(AB = 2\). Khoảng cách từ \(A\) đến mặt phẳng \(\left( {A'BC} \right)\) bằng
Đáp án đúng là: B
Dựng \(AH \bot A'B \Rightarrow AH \bot \left( {A'BC} \right)\).
\( \Rightarrow d\left( {A;\left( {A'BC} \right)} \right) = AH\).
Tìm độ dài đoạn \(AH\).
Đáp án cần chọn là: B
Có bao nhiêu giá trị nguyên của tham số m sao cho hàm số $f(x) = \dfrac{1}{3}x^{3} + mx^{2} + 4x + 3$ đồng biến trên $\mathbb{R}$.
Đáp án đúng là: 5
$\left. f'(x) \geq 0,\forall x \in {\mathbb{R}}\Leftrightarrow\Delta' \leq 0 \right.$
Đáp án cần điền là: 5
Trong không gian với hệ tọa độ \(Oxyz,\) cho hai điểm \(A\left( {2;0; - 1} \right)\), \(B\left( {1; - 1;3} \right)\) và mặt phẳng \(\left( P \right):3x + 2y - z + 5 = 0\). Gọi \(\left( \alpha \right)\) là mặt phẳng đi qua \(A,B\) và vuông góc với \(\left( P \right),\) phương trình của mặt phẳng \(\left( \alpha \right)\) có dạng: \(ax + by + z + d = 0\). Tính tổng \(T = a + b + d\)
Đáp án đúng là: B
Viết phương trình mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(A\) và nhận \(\left[ {\overrightarrow {AB} ,{{\overrightarrow n }_{\left( P \right)}}} \right]\) là vecto pháp tuyến .
Đáp án cần chọn là: B
Trong không gian \(Oxyz\), toạ độ điểm \(H\) là hình chiếu của điểm \(M\left( {2;0;1} \right)\) lên đường thẳng \(d:\dfrac{{x - 1}}{1} = \dfrac{y}{2} = \dfrac{{z - 2}}{1}\) là
Đáp án đúng là: D
+) Viết phương trình mp\(\left( P \right)\) qua \(M\left( {2;0;1} \right)\) và vuông góc với đường thẳng \(d\).
+) Điểm \(H\) là hình chiếu của điểm \(M\) lên đường thẳng \(d\) nên \(H\) là giao điểm của \(\left( P \right)\) và \(d\). Tham số hóa tọa độ điểm \(H\) theo phương trình đường thẳng \(d\). Thay tọa độ điểm \(H\) vào phương trình mp\(\left( P \right)\), giải phương trình tìm tham số \(t\). Từ đó, kết luận tọa độ điểm \(H\).
Đáp án cần chọn là: D
Một trạm viễn thông S có tọa độ (5;1). Một người đang ngồi trên chiếc xe khách chạy trên đoạn cao tốc có dạng một đường thẳng \(\Delta \) có phương trình \(12x + 5y - 20 = 0\). Tính khoảng cách ngắn nhất giữa người đó và trạm viễn thông S. Biết rằng mỗi đơn vị đo độ dài tương ứng với 1km. (nhập đáp án vào ô trống, kết quả viết dưới dạng phân số tối giản a/b).

Đáp án đúng là: 45/13
Khoảng cách ngắn nhất bằng khoảng cách từ S đến đường thẳng \(\Delta \).
Đáp án cần điền là: 45/13
Một tập đoàn định đầu tư vào hai dự án. Giả sử, dự án đầu tư đầu có tốc độ sinh lợi nhuận là \(P_1(t)=50+t^2\) (đồng/năm), dự án thứ hai có tốc độ sinh lợi nhuận là \(P_2(t)=200+5 t\) (đồng/năm). Sau \(t\) năm thì tốc độ sinh lời của dự án hai bằng một nửa dự án một. Tính lợi nhuận thực tế trong khoảng thời gian trên (kết quả làm tròn đến hàng đơn vị).
Đáp án đúng là: 6675
Ứng dụng tích phân tính lợi nhuận thực tế.
Đáp án cần điền là: 6675
Trong không gian, cho mặt phẳng \(\left( P \right):\,\,x + 3y - 2z + 1 = 0\) và đường thẳng \(d:\,\,\dfrac{{x - 1}}{2} = \dfrac{{y + 1}}{{ - 1}} = \dfrac{{z - 4}}{1}\). Phương trình đường thẳng \(\Delta \) đi qua điểm \(A\left( {1;2;1} \right)\) cắt mặt phẳng \(\left( P \right)\) và đường thẳng \(d\) lần lượt tại \(B,\,\,C\) sao cho \(C\) là trung điểm của \(AB\) là
Đáp án đúng là: D
- Tìm tọa độ \(C\) theo \(t\) với \(t \in \mathbb{R}\).
- Tìm tọa độ \(B\) theo \(t\) dựa vào giả thiết \(C\) là trung điểm của \(AB\).
- Từ giả thiết \(B \in \left( P \right)\) tìm được \(t\).
- Viết phương trình đường thẳng \(\Delta \).
Đáp án cần chọn là: D
Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng).
| Doanh thu | $\left\lbrack {5;7} \right)$ | $\left\lbrack {7;9} \right)$ | $\left\lbrack {9;11} \right)$ | $\left\lbrack {11;13} \right)$ | $\left\lbrack {13;15} \right)$ |
| Số ngày | 2 | 7 | 7 | 3 | 1 |
Tứ phân vị thứ ba của mẫu số liệu trên gần nhất với giá trị nào trong các giá trị sau?
Đáp án đúng là: D
Tìm cỡ mẫu xác định nhóm chứa phân vị thứ i từ đó tính $Q_{i} = u_{m} + \dfrac{\dfrac{in}{4} - C}{n_{m}}\left( {u_{m + 1} - u_{m}} \right)$
Đáp án cần chọn là: D
Cho một cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu tiên \({u_1} = 1\) và tổng \(100\) số hạng đầu bằng \(24850\). Tính \(S = \dfrac{1}{{{u_1}{u_2}}} + \dfrac{1}{{{u_2}{u_3}}} + \dfrac{1}{{{u_3}{u_4}}} + ...... + \dfrac{1}{{{u_{49}}{u_{50}}}}\).
Đáp án đúng là: D
- Tìm CSC đã cho bằng cách sử dụng công thức \({S_n} = \dfrac{{n\left[ {2{u_1} + \left( {n - 1} \right)d} \right]}}{2}\)
- Thay vào tổng đã cho tính toán.
Đáp án cần chọn là: D
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = 2x - 3,\forall x \in {\bf{R}}\) và \(f\left( 0 \right) = 0\). Tính diện tích hình phẳng \(S\) giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường \(x = - 15;\,x = 15\).
Đáp án đúng là: D
Cho \(a,\,\,b,\,\,c\) là các số thực dương thỏa mãn \({a^2} = 9bc\). Tính \(S = 2{\log _3}a - {\log _3}b - {\log _3}c\).
Đáp án đúng là: D
Sử dụng công thức:
\(\begin{array}{l} + \,\,{\log _a}\left( {xy} \right) = {\log _a}x + {\log _a}y,\,\,\forall a,x,y > 0\\ + \,\,{\log _a}\left( {{x^\alpha }} \right) = \alpha {\log _a}x,\,\,n \in \mathbb{R}\end{array}\)
Đáp án cần chọn là: D
Trong không gian với hệ trục toạ độ \(Oxyz\), cho \(\vec a = \left( { - 1;2;0} \right),\vec b = \left( {2;1;0} \right),\vec c = \left( {3; - 1; - 1} \right)\). Tìm toạ độ của véctơ \(\vec u = \vec a + 3\vec b + 2\vec c\).
Đáp án đúng là: D
Sử dụng quy tắc cộng hai vec tơ và nhân vec tơ với một số thực.
Đáp án cần chọn là: D
Tích phân $I = {\int_{- 2}^{0}\left| \dfrac{x^{2} - x - 2}{x - 1} \right|}dx = a + b\ln c$. Khi đó $a + b + c$ bằng
Đáp án đúng là: 4
Tách tích phân thành từng khoảng ${\int_{a}^{b}f}(x)dx = {\int_{a}^{x_{1}}f}(x)dx + {\int_{x_{1}}^{x_{2}}f}(x)dx + \cdots$
Nếu $P(x) \geq 0$ thì $\left| P(x) \middle| = P(x) \right.$.
Nếu $P(x) \leq 0$ thì $\left| P(x) \middle| = - P(x) \right.$.
Giải phương trình $\dfrac{x^{2} - x - 2}{x - 1} = 0$ để tìm các điểm tách tích phân
Đáp án cần điền là: 4
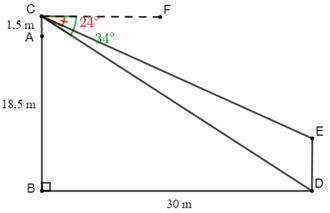
Từ trên nóc của một tòa nhà cao 18,5m, bạn Nam quan sát một cái cây cách tòa nhà 30m và dùng giác kế đo được góc lệch giữa phương quan sát gốc cây và phương nằm ngang là 34°, góc lệch giữa phương quan sát ngọn cây và phương nằm ngang là 24°. Biết chiều cao của chân giác kế là 1,5m. Chiều cao của cái cây là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
Đáp án đúng là: 6,9
Giả sử toà nhà là AB = 18,5m; giác kế AC = 1,5m; chiều cao của cái cây là DE; khoảng cách từ tòa nhà tới cây là BD = 30m.
Góc tạo bởi phương quan sát gốc cây và phương nằm ngang là \(\widehat {FCD} = {34^0}\), góc tạo bởi phương quan sát ngọn cây và phương nằm ngang là \(\widehat {FCE} = {24^0}\).
Ta cần tính DE.
Đáp án cần điền là: 6,9
Số nghiệm của phương trình sin2x – 2cosx = 0 thuộc đoạn \(\left[ { - \dfrac{{5\pi }}{2};\dfrac{\pi }{2}} \right]\) là:
Đáp án đúng là: B
- Sử dụng công thức nhân đôi: sin2x = 2sinxcosx.
- Sử dụng phương pháp đưa về phương trình tích.
Đáp án cần chọn là: B
Có bao nhiêu giá trị của tham số $m$ để giá trị lớn nhất của hàm số $y = \dfrac{x - m^{2} - 2}{x - m}$ trên đoạn $\left\lbrack {0;4} \right\rbrack$ bằng $- 1$? (nhập đáp án vào ô trống)
Đáp án đúng là: 1
Đạo hàm và tím gtln theo tham số m.
Đáp án cần điền là: 1
Một chiếc hộp có 50 viên bi, trong đó có 30 viên bi màu xanh và 20 viên bi màu đỏ, các viên bi có kích thước và khối lượng giống nhau. Sau khi kiểm tra, người ta thấy có 70% số viên bi màu xanh được đánh số và 60% số viên bi màu đỏ được đánh số, những viên bi còn lại không đánh số. Lấy ngẫu nhiên một viên bi từ hộp đó. Biết rằng, viên bi lấy ra được đánh số, xác suất để viên bi đó có màu xanh bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
Đáp án đúng là: A
A: “Viên bi lấy ra được đánh số”
B: “Viên bi có màu xanh”
Áp dụng công thức xác suất toàn phần, công thức Bayes.
Đáp án cần chọn là: A
Hàm số nào dưới đây là một nguyên hàm của hàm số \(f\left( x \right) = {e^{2x + 2022}}\)?
Đáp án đúng là: A
\(\int {{e^{ax + b}}\,{\rm{d}}x = } \dfrac{1}{a}{e^{ax + b}} + C\,\,\left( {a \ne 0} \right)\).
Đáp án cần chọn là: A
Thời gian truy cập internet mỗi buổi tối của một số học sinh lớp 12 được cho trong bẳng sau

Số trung vị $M_{e}$ của mẫu số liệu ghép nhóm này là
Đáp án đúng là: B
Tứ phân vị thứ $i$, kí hiệu là $Q_{i}$ với $i = 1,2,3$ của mẫu số liệu ghép nhóm được xác định như sau:
$Q_{i} = u_{m} + \dfrac{\dfrac{in}{4} - C}{n_{m}}\left( {u_{m + 1} - u_{m}} \right).$
Trong đó:
+ $n = n_{1} + n_{2} + ... + n_{k}$ là cỡ mẫu.
+ $\left\lbrack {u_{m};u_{m + 1}} \right)$ là nhóm chứa tứ phân vị thứ $i.$
+ $n_{m}$ là tần số của nhóm chứa tứ phân vị thứ $i.$
+ $C = n_{1} + n_{2} + ... + n_{m - 1}.$
Trung vị của mẫu số liệu ghép nhóm $M_{e} = Q_{2}$
Đáp án cần chọn là: B
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông tại \(A,\,\,AB = a,\,\,BC = 2a\) và \(SB\) vuông góc với mặt phẳng \(\left( {ABC} \right)\). Biết góc giữa hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SBC} \right)\) bằng \({60^0}\). Thể tích của khối chóp \(S.ABC\) bằng
Đáp án đúng là: B
- Dựng góc giữa hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SBC} \right)\).
- Tính \(SB\).
- Tính thể tích của khối chóp.
Đáp án cần chọn là: B
Trong không gian \(Oxyz\), cho các điểm \(A\left( {3; - 1;2} \right),B\left( {1;1;2} \right),C\left( {1; - 1;4} \right)\), đường tròn \(\left( C \right)\) là giao tuyến của mặt phẳng \(\left( P \right):x + y + z - 4 = 0\) và mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 4x - 6z + 10 = 0\). Hỏi có bao nhiêu điểm \(M\) thuộc đường tròn \(\left( C \right)\) sao cho \(T = MA + MB + MC\) đạt giá trị lớn nhất?
Đáp án đúng là: A
Kiểm tra tọa độ các điểm \(A\left( {3; - 1;2} \right),B\left( {1;1;2} \right),C\left( {1; - 1;4} \right)\) ta thấy \(A,B,C \in \left( P \right) \cap \left( S \right) \Rightarrow A,B,C \in \left( C \right)\).
Đồng thời \(AB = BC = AC \Rightarrow \Delta ABC\) đều.
Từ đó, biện luận vị trí của \(M\) thuộc đường tròn \(\left( C \right)\) sao cho \(T = MA + MB + MC\) đạt giá trị lớn nhất.
Đáp án cần chọn là: A
Cho hàm số \(y = 2{x^3} + 3{x^2} - 4x + 5\) có đồ thị là (C). Trong số các tiếp tuyến của (C) có một tiếp tuyến có hệ số góc nhỏ nhất. Hệ số góc của tiếp tuyến này bằng:
Đáp án đúng là: B
Hệ số góc của tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ \(x = {x_0}\) là \(k = f'\left( {{x_0}} \right)\).
Tìm GTNN bằng cách sử dụng hằng đẳng thức để đánh giá.
Đáp án cần chọn là: B
Cho hàm số f(x) có đạo hàm \(f'\left( x \right) = {\left( {x + 1} \right)^2}{\left( {x - 1} \right)^3}\left( {2 - x} \right)\), Hàm số y = f(x) đồng biến trên khoảng nào, trong các khoảng dưới đây?
Đáp án đúng là: B
Lập BXD f’(x).
Đáp án cần chọn là: B
Cho hàm số \(f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và có bảng biến thiên như sau:
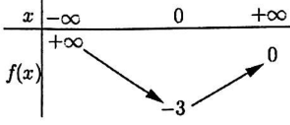
Hàm số \(g\left( x \right) = \dfrac{{f\left( x \right)}}{{{x^3}}}\) có bao nhiêu điểm cực trị trên khoảng \(\left( {0; + \infty } \right)\)?
Đáp án đúng là: D
Tính đạo hàm của hàm $g(x)$ và chứng minh hàm số luôn đồng biến
Đáp án cần chọn là: D
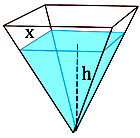
Dựa vào dữ liệu dưới đây, thí sinh lựa chọn một phương án đúng theo yêu cầu của câu dưới đây:
Một cái bể nước có dạng khối chóp tứ giác đều ngược với cạnh đáy bằng $3\sqrt{2}\,\, dm$ và chiều cao bằng $6\,\, dm$ (tham khảo hình vẽ bên). Nước được bơm vào bể với tốc độ không đổi là 2 lít/phút và ban đầu bể không chứa nước (các kết quả bên dưới được làm tròn đến hai chữ số thập phân sau dấu phẩy).
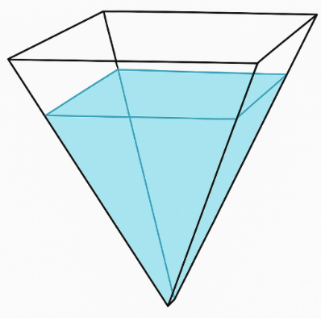
Trả lời cho các câu 48, 49, 50 dưới đây:
Thời gian để bể nước được bơm đầy là
Đáp án đúng là: A
Tính thể tích bể nước $V = \dfrac{1}{3}h.S$ từ đó tính thời gian đầy bể
Đáp án cần chọn là: A
Khi thể tích nước trong bể bằng $\dfrac{1}{3}$ thể tích của bể, tốc độ dâng lên của nước là
Đáp án đúng là: C
Tính thể tích bể nước theo chiều cao h ở thời điểm bất kì.
Lấy đạo hàm 2 vế từ đó tìm tốc độ dâng của nước.
Đáp án cần chọn là: C
Khi mực nước cách miệng bể 0,5 dm, người ta ngừng bơm và bắt đầu xả nước ra với ước lượng tốc độ giảm chiều cao của mực nước trong bể theo thời gian $t$ (phút) được mô hình hóa bởi hàm số $h'(t) = \dfrac{1}{350}t - \dfrac{193}{700}$ (dm/phút). Lượng nước xả ra sau 5 phút là
Đáp án đúng là: C
Tính chiều cao của mực nước khi lượng nước xả sau 5 phút
Lượng nước xả sau 5 phút là hiệu thể tích thời điểm chiều cao 5,5 và thời điểm mà nước xả 5 phút.
Đáp án cần chọn là: C
Phần 2: Văn học - Ngôn Ngữ
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án đúng là: C
Căn cứ vào nghĩa của từ.
Dạng bài tìm từ khác loại
Đáp án cần chọn là: C
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án đúng là: B
Căn cứ vào nghĩa của từ.
Dạng bài tìm từ khác loại
Đáp án cần chọn là: B
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án đúng là: A
Căn cứ vào nghĩa của từ.
Dạng bài tìm từ khác loại
Đáp án cần chọn là: A
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án đúng là: D
Căn cứ vào nghĩa của từ.
Dạng bài tìm từ khác loại
Đáp án cần chọn là: D
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án đúng là: D
Căn cứ vào nghĩa của từ.
Dạng bài tìm từ khác loại
Đáp án cần chọn là: D
Chọn từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây.
_______ là biện pháp tu từ, theo đó, người nói người viết kể ra nhiều sự vật, sự việc, hoạt động, tính chất, trạng thái... trong cùng một câu, một đoạn để tạo nên _________ mạnh, hiệu quả cao trong miêu tả, kể chuyện hoặc biểu lộ tình cảm, cảm xúc.
Đáp án đúng là: B
Căn cứ hiểu biết về nội dung câu văn
Dạng bài điền từ
Đáp án cần chọn là: B
Chọn từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây.
Thơ Nôm Hồ Xuân Hương là tiếng nói quyết liệt đấu tranh cho quyền được hưởng hạnh phúc của người ______, thể hiện nỗi thương cảm với _________ và khẳng định, đề cao vẻ đẹp, khát vọng của họ.
Đáp án đúng là: A
Căn cứ hiểu biết về nội dung câu văn
Dạng bài điền từ
Đáp án cần chọn là: A
Chọn từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây.
Các electron chuyển động nhanh đến mức mọi nỗ lực của con người để “giữ chân” nó đều vô hiệu, ________ việc nhìn vào nó ở một mảnh cực nhỏ của một giây thì có thể. _________ các nhà khoa học có thể có một cái nhìn “mờ” về chúng và mở ra một thứ khoa học hoàn toàn mới.
Đáp án đúng là: D
Căn cứ hiểu biết về nội dung câu văn
Dạng bài điền từ
Đáp án cần chọn là: D
Chọn từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây.
Trong những hình thức giao tiếp khác, nhiều trường hợp, người ta chỉ cần hoặc chỉ có thể sử dụng phương tiện ________ (dùng đèn giao thông, vẫy cờ, ra hiệu vì không tiện nói, mỉm cười....) để giao tiếp mà vẫn đạt hiệu quả.
Đáp án đúng là: D
Căn cứ hiểu biết về nội dung câu văn
Dạng bài điền từ
Đáp án cần chọn là: D
Chọn từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây.
Với một nếp sống phong lưu về vật chất, phong phú về tinh thần, lịch sử ngàn năm văn vật của Thăng Long – Đông Đô – Hà Nội đã hun đúc cho người Hà Nội một nếp sống _________: từng trải mà nhẹ nhàng, kiên định mà duyên dáng, hào hoa mà thanh thoát, sang trọng mà không xa hoa, cởi mở mà không lỗ bịch, nhố nhăng.... từ lời ăn tiếng nói đến phong cách làm ăn, suy nghĩ...
Đáp án đúng là: C
Căn cứ hiểu biết về nội dung câu văn
Dạng bài điền từ
Đáp án cần chọn là: C
Xác định một từ cụm từ SAI về ngữ pháp hoặc ngữ nghĩa logic phong cách:
Bắt đầu vào mùa xuân, những ruộng cải bên kia sông đã nhuộm vàng cả cánh đồng.
Đáp án đúng là: B
Căn cứ vào ngữ pháp, ngữ nghĩa, logic, phong cách
Dạng bài tìm lỗi sai
Đáp án cần chọn là: B
Xác định một từ/cụm từ SAI về ngữ pháp hoặc ngữ nghĩa logic/phong cách.
Về cấu trúc truyện ngắn hiện đại thường có sự chuyển đổi linh hoạt điểm nhìn và sử dụng ngôn ngữ gần gũi với đời thường trong đó việc miêu tả nét riêng của ngôn ngữ nhân vật được đặc biệt chú trọng.
Đáp án đúng là: A
Căn cứ vào nghĩa của từ, ngữ cảnh.
Đáp án cần chọn là: A
Xác định một từ/cụm từ SAI về ngữ pháp hoặc ngữ nghĩa logic/phong cách.
Năm 1941, Factors of Soil Formation (Các yếu tố hình thành đất) của Hans Jenny (1899 – 1992), một hệ thống của thổ nhưỡng học định lượng, đã tổng quát hóa một cách xúc tích và minh họa rất nhiều nguyên lý cơ bản của khoa học đất hiện đại cho tới ngày đó.
Đáp án đúng là: B
Căn cứ vào ngữ pháp, ngữ nghĩa, logic, phong cách
Dạng bài tìm lỗi sai
Đáp án cần chọn là: B
Xác định một từ/cụm từ SAI về ngữ pháp hoặc ngữ nghĩa logic/phong cách.
Trong thời kỳ trứng nước của y học hiện đại, Việt Nam cũng đã tham gia thực hiện những nghiên cứu về lao chứ không chủ động chờ đợi phương thức điều trị từ mẫu quốc.
Đáp án đúng là: C
Căn cứ vào ngữ pháp, ngữ nghĩa, logic, phong cách
Dạng bài tìm lỗi sai
Đáp án cần chọn là: C
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa logic/phong cách.
Ngôn ngữ viết tồn tại trong các văn bản xuất hiện dưới nhiều hình thức vật thể khác nhau: bản viết tay, bản đánh máy, bản in, bản vẽ, bản chữ nổi dành cho người khiếm thị...
Đáp án đúng là: D
Căn cứ vào ngữ pháp, ngữ nghĩa, logic, phong cách
Dạng bài tìm lỗi sai
Đáp án cần chọn là: D
Đọc đoạn trích dưới đây và trả lời các câu hỏi 66 đến 70:
Trong ý nghĩ của công chúng, hoạt động khoa học thường được coi là một việc làm hoàn toàn duy lí chỉ dựa trên logic thuần túy và tước bỏ mọi cảm xúc, và vật lí cũng là một môn khoa học nên hoàn toàn không biết đến thưởng ngoạn cái đẹp. Nó không có quyền đưa ra những đánh giá tốt, xấu, mà chỉ tính đến những sự kiện chính xác, lạnh lùng và khách quan. Tuy nhiên, dù là một nhà khoa học nhưng tôi vẫn nhạy cảm với cái đẹp và sự hài hòa của thiên nhiên như một nhà thơ hay một họa sĩ. Trong công việc, ngoài những suy ngẫm, cân nhắc ở cấp độ lí trí ra, tôi vẫn thường để mình bị dẫn dắt bởi những suy ngẫm mĩ học. Ý nghĩ cho rằng công việc của một nhà khoa học hoàn toàn không có xúc cảm là hết sức sai lầm. Con người luôn có lí trí và tình cảm, và nhà khoa học, cũng như bất kì ai, không thể tách rời những cảm xúc của mình ra khỏi lí trí khi tìm cách đối thoại với tự nhiên. Các nhà bác học vĩ đại nhất cũng đều đưa ra ý kiến rõ ràng về vai trò của cái đẹp đối với khoa học. Chẳng hạn, nhà toán học người Pháp Henri Poincaré đã nói: “Nhà khoa học không nghiên cứu tự nhiên vì mục đích vụ lợi. Anh ta nghiên cứu nó vì tìm thấy ở đó niềm vui sướng; và anh ta tìm thấy niềm vui sướng bởi vì tự nhiên rất đẹp. Nếu tự nhiên không đẹp, nó sẽ không đáng để nghiên cứu, và cuộc đời cũng sẽ không đáng sống.” Tôi hoàn toàn tán thành ý kiến này. Đối với tôi, niềm đam mê nghiên cứu thực tại, không nghi ngờ gì nữa, được thúc đẩy trước tiên bởi sự cảm nhận cái đẹp của thế giới.
(Trịnh Xuân Thuận, Vũ trụ và hoa sen, NXB Tri thức, Hà Nội, 2015)
Trả lời cho các câu 66, 67, 68, 69, 70 dưới đây:
Mục đích chính của tác giả trong đoạn trích này là gì?
Đáp án đúng là: B
Căn cứ vào nội dung toàn đoạn trích.
Đáp án cần chọn là: B
Từ nào dưới đây trái nghĩa với từ “duy lí” (gạch chân, in đậm) trong đoạn trích trên?
Đáp án đúng là: A
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: A
Đoạn trích trên nổi bật với những thao tác lập luận nào dưới đây?
Đáp án đúng là: D
Căn cứ vào nội dung của văn bản.
Đáp án cần chọn là: D
Theo tác giả, mục đích đầu tiên khiến tác giả nghiên cứu khoa học là gì?
Đáp án đúng là: C
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: C
Thông tin nào KHÔNG được suy ra từ bài đọc trên?
Đáp án đúng là: A
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: A
Đọc đoạn trích sau đây và trả lời 5 câu hỏi sau:
Chim ô tác kori (Ardeotis kori) là loài chim bay nặng nhất thế giới với con đực lớn cỡ 11 - 19 kg và có sải cánh 2,75 m. Sách kỷ lục Thế giới Guinness cho biết mẫu vật lớn nhất thuộc loài chim ô tác kori nặng 18,14 kg. Con chim này bị bắn trúng ở Nam Phi và ghi nhận năm 1936. Theo Vườn thú quốc gia Smithsonian, chim cái nhỏ bằng một nửa con đực. Loài chim này sống ở hai khu vực riêng biệt tại Nam Phi và Đông Phi, dành phần lớn thời gian kiếm ăn trên mặt đất. Chế độ ăn của chúng khá đa dạng, bao gồm côn trùng, bò sát và chuột nhỏ tới hạt, quả mọng và rễ cây. Liên minh Bảo tồn Thiên nhiên Quốc tế (IUCN) xếp chim ô tác kori vào nhóm sắp bị đe dọa và mô tả chúng là loài tĩnh lặng, chỉ di chuyển loanh quanh trong vùng. Loài chim bay nặng thứ hai trên thế giới cũng thuộc họ ô tác. Đó là chim ô tác lớn (Otis tarda). Chúng chỉ nhẹ cân hơn chim ô tác kori một chút, với trọng lượng tối đa khoảng 6 - 18 kg. Khác với chim ô tác kori không di cư và hiếm khi bay rất xa, chim ô tác lớn có hành trình di cư khứ hồi hơn 4.000 km giữa nơi sinh sản ở Mông Cổ và nơi sinh sống vào mùa đông ở Trung Quốc. Chim ô tác lớn cũng thể hiện dị hình giới tính và có thể sở hữu chênh lệch kích thước lớn nhất giữa con đực và con cái trong thế giới loài chim. Con đực nặng gấp 4 lần so với con cái. Ngược lại, loài chim nặng nhất thế giới không bay được là phân loài ở Nam Phi của chim đà điểu. Chim đà điểu Nam Phi (Struthio camelus australis) có thể nặng 156 kg. Loài động vật có vú bay được nặng nhất là cáo bay, nặng 0,5 - 1 kg, tùy theo loài cụ thể.
(An Khang, Loài chim nặng nhất thế giới, Báo điện tử Vnexpress, ngày 5/7/2024)
Trả lời cho các câu 71, 72, 73, 74, 75 dưới đây:
Mục đích chính của bài đọc trên là gì?
Đáp án đúng là: B
Căn cứ vào kiến thức về kiểu văn bản. Nội dung thông điệp
Đáp án cần chọn là: B
Bài đọc trên thuộc loại văn bản nào dưới đây?
Đáp án đúng là: C
Căn cứ vào nội dung đoạn trích.
Đáp án cần chọn là: C
Điểm khác biệt lớn nhất giữa chim ô tác kori và chim ô tác lớn là gì?
Đáp án đúng là: C
Căn cứ vào nội dung của đoạn trích.
Đáp án cần chọn là: C
Thông tin nào sau đây KHÔNG THỂ suy ra từ nội dung của đoạn trích?
Đáp án đúng là: C
Căn cứ vào nội dung đoạn trích.
Đáp án cần chọn là: C
Chim ô tác kori có chế độ ăn như thế nào?
Đáp án đúng là: D
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: D
Đọc đoạn trích và trả lời câu hỏi dưới đây.
Những bài viết của giáo sư Võ Tòng Xuân đăng tải trên Tia Sáng được ông rút ruột từ những nghiên cứu, báo cáo và quan sát thực địa của mình. Nếu nhìn xuyên suốt toàn bộ sự nghiệp nghiên cứu của ông, có thể thấy chủ đề lúa gạo, ĐBSCL, chính sách lương thực, an ninh lương thực, nghiên cứu nông nghiệp, sản xuất lúa gạo, mô hình kinh tế nông nghiệp... trở đi trở lại. Dường như mục tiêu của cuộc đời ông đặt vào những chữ tưởng chừng giản dị: làm sao cho sinh kế của người nông dân, đặc biệt người nông dân ĐBSCL bền vững?
(Thanh Nhàn, Giáo sư Võ Tòng Xuân: Cây lúa thơm đã về với đất mẹ, Tạp chí Tia sáng, ngày
Những nghiên cứu của giáo sư Võ Tòng Xuân đều hướng tới mục tiêu lớn nhất là gì?
Đáp án đúng là: C
Căn cứ vào nội dung đoạn trích.
Dạng bài đọc hiểu tác phẩm văn học
Đáp án cần chọn là: C
Đọc đoạn thơ và trả lời câu hỏi dưới đây.
chúng tôi qua cái khắc nghiệt mùa khô
qua mùa mưa mùa mưa dai dẳng
võng mắc cột tràm đêm ướt sũng
xuồng vượt sông dưới pháo sáng nhạt nhoà
đôi lúc ngẩn người. ma
đôi lúc ngẩn người... một ráng đỏ chiều xa
quên đời mình thêm tuổi
chân dép lốp đạp mòn trăm ngọn núi
mà không hề rợp bóng xuống tương lai
(Thanh Thảo, Một người lính nói về thế hệ mình, In trong Khối vuông ru-bích, NXB Tác phẩm mới, Hà Nội, 1985)
Câu thơ “chân dép lốp đạp mòn trăm ngọn núi” nổi bật với biện pháp tu từ nào?
Đáp án đúng là: C
Căn cứ vào nội dung đoạn trích.
Dạng bài đọc hiểu tác phẩm văn học
Đáp án cần chọn là: C
Đọc bài thơ và trả lời câu hỏi dưới đây.
Hoa hồng nở hoa hồng lại rụng,
Hoa tàn, hoa nở cũng vô tình;
Hương hoa bay thấu vào trong ngục,
Kể với tù nhân nỗi bất bình.
(Hồ Chí Minh, Cảnh chiều hôm, Hồ Chí Minh toàn tập, tập 3, (Nam Trân địch), NXB Chính trị)
Hương hoa “bất bình” về điều gì?
Đáp án đúng là: D
Căn cứ vào nội dung đoạn trích.
Dạng bài đọc hiểu tác phẩm văn học
Đáp án cần chọn là: D
Đọc đoạn trích và trả lời câu hỏi dưới đây.
Một tiếng ào dữ dội. Như một đàn cá voi lớn, sóng trào qua ngọn những cây vẹt cao nhất, vụt vào thân đê rào rào. Một vài người giật mình quăng quang gánh, ngã sấp. Họ đứng dậy, mặt tái mét. Một cuộc vật lộn dữ dội diễn ra. Một bên là biển, là gió, trong một cơn giận dữ điên cuồng, hung hăng xông vào, bẻ nát, đập tan, biến thành nước những gì vướng víu. Một bên là hàng ngàn người với hai bàn tay, và những dụng cụ thô sơ, với tinh thần quyết tâm chống giữ. Cái đáng sợ chưa hẳn là biển và gió, mà là tinh thần bị chùn nhụt, ngã lòng trước nguy hiểm. Sóng vào một đợt, hai đợt. Một người, hai người, rồi mười người, ba bốn chục người quẳng đất trên vai, ào chạy.
(Chu Văn, Bão biển, tập 2, NXB Hội Nhà văn, Hà Nội, 2007)
Theo đoạn trích, trở ngại lớn nhất trong cuộc đời đến từ đâu?
Đáp án đúng là: C
Căn cứ vào nội dung đoạn trích.
Dạng bài đọc hiểu tác phẩm văn học
Đáp án cần chọn là: C
Đọc văn bản và trả lời câu hỏi dưới đây.
Hồi yêu nhau. Có lần gọt trái cây cho nàng, anh bị đứt tay. Nàng mặt mày tái mét, ôm cả cánh tay anh hốt hoảng đòi đưa đi ... bác sĩ!
Lấy nhau rồi. Một lần thấy tấm hình cưới sắp bị rớt, anh mang búa đinh ra sửa. Loay hoay sợ đụng bể kiếng, búa đập vào tay. Máu tóe ra. Anh xuýt xoa nhờ nàng lấy giùm bông băng, nàng bực bội: Sao anh vụng thế! Chồng với chả con!
Vết đứt tay ngày xưa giờ bỗng thấm đau, đau thấy 36 ông trời!
(Nguyễn Thị Hậu, Vết đau, in trong 101 truyện 100 chữ, NXB Hội Nhà văn, Thành phố Hồ Chí Minh, 2012)
Trong văn bản trên, người chồng cảm thấy đau nhất khi nào?
Đáp án đúng là: D
Căn cứ vào nội dung đoạn trích.
Dạng bài đọc hiểu tác phẩm văn học
Đáp án cần chọn là: D
Đọc đoạn trích và trả lời câu hỏi dưới đây.
Đầy vườn cỏ mọc, lau thưa,
Song trăng quạnh quẽ, vách mưa rã rời,...
Trước sau nào thấy bóng người,
Hoa đào năm ngoái còn cười gió đông.
Sập sè én liệng lầu không,
Cỏ lan mặt đất, rêu phong dấu giày.
Cuối tường gai góc mọc đầy,
Đi về này những lỗi này năm xưa!
Chung quanh lặng ngắt như tờ,
Nỗi niềm tâm sự bây giờ hỏi ai?
(Nguyễn Du, Truyện Kiều, trong Đào Duy Anh, Từ điển Truyện Kiều, NXB Khoa học xã hội, Hà
Đoạn thơ trên nổi bật với bút pháp nghệ thuật nào?
Đáp án đúng là: B
Căn cứ vào nội dung đoạn trích.
Dạng bài đọc hiểu tác phẩm văn học
Đáp án cần chọn là: B
Đọc đoạn trích và trả lời câu hỏi dưới đây.
Những kết quả nghiên cứu này gợi ý rằng thực hành tôn giáo, tâm linh có ảnh hưởng đa chiều đến sức khỏe tinh thần, không phải luôn mang đến ảnh hưởng tích cực. Do vậy, ứng dụng tôn giáo trong việc điều trị và hỗ trợ tâm lý cần nhiều sự cẩn trọng. Nhiều người gồng mình trước các nỗi đau về tinh thần và bất lực trong cuộc sống muốn tìm đến tôn giáo để tìm kiếm sự an ủi, niềm hy vọng, ý nghĩa cuộc đời nhưng không phải lúc nào họ cũng tìm được sự thanh thản và bình an. Đối với một số người, thực hành tôn giáo càng khiến các triệu chứng tâm thần trầm trọng hơn, họ càng trở nên sợ hãi, tội lỗi, khổ sở và thậm chí còn dùng tôn giáo như một cái cớ để từ chối và gạt bỏ bất cứ thay đổi khác, dù là tích cực trong đời sống.
(Đặng Hoàng Ngân, Ứng dụng Phật giáo trong nâng cao sức khỏe tinh thần: Con dao hai lưỡi?, Tạp chí Tia sáng, ngày 29/08/2024)
Nội dung chính của đoạn trích trên là gì?
Đáp án đúng là: A
Căn cứ vào nội dung đoạn trích.
Dạng bài đọc hiểu tác phẩm văn học
Đáp án cần chọn là: A
Đọc đoạn trích sau và trả lời câu hỏi:
Chị bế con rón rén bước vào chỗ chõng nằm. Thằng bé vẫn sụt sịt. Anh đĩ Chuột giờ mình, hơi nghiêng mặt quay ra. Một làn ánh sáng mờ lướt qua làm cho cái mặt hốc hác và màu da đã xanh lại càng xanh thêm. Mái tóc dài quá xoà xuống tai và cổ, hai con mắt ngơ ngác và lờ đờ, những chiếc răng dài và thưa ở cái mồm hé ra để cho dễ thở khiến anh có cái vẻ dễ sợ của con ma đói. Thấy vợ con, anh cố gượng nhếch miệng cố gượng một cái cười méo xệch và vừa thở phều phào vừa hỏi bằng một thứ tiếng yếu ớt như từ thế giới bên kia đưa lại.
(Nghèo, Tuyển tập Nam Cao, NXB Hội nhà văn, 1993)
Yếu tố miêu tả trong đoạn trích trên có tác dụng gì?
Đáp án đúng là: B
Căn cứ vào nội dung đoạn trích.
Dạng bài đọc hiểu tác phẩm văn học
Đáp án cần chọn là: B
Đọc đoạn trích sau và trả lời câu hỏi:
Sự vô cảm là gì? Theo từ nguyên, nó có nghĩa là “không có cảm xúc”. Đó là một trạng thái lạ lùng và trái tự nhiên, một trạng thái mà trong đó đường ranh giữa sáng và tối, bình minh và hoàng hôn, tội ác và hình phạt, tàn bạo và nhân đạo, tốt và xấu bị mờ đi. Tiến trình của vô cảm và những hậu quả không thể tránh được của nó là gì? Vô cảm có phải là một triết lý sống hay không? Có cái gọi là triết lý vô cảm hay không? Liệu ta có thể xem vô cảm là một đức tính không? Có phải đôi lúc chúng ta cũng cần áp dụng vô cảm để giữ cho mình không bị hóa điên, để sống một cách bình thường, để thưởng thức một bữa ăn và cốc rượu ngon, khi thế giới quanh ta đang trải qua những biến động tang thương?
(Elie Wiesel, Sự nguy hiểm của vô cảm: Những bài học rút ra từ một thế kỷ đầy bạo động)
Thao tác lập luận chính trong đoạn trích trên là gì?
Đáp án đúng là: A
Căn cứ vào nội dung đoạn trích.
Dạng bài đọc hiểu tác phẩm văn học
Đáp án cần chọn là: A
Đọc đoạn trích sau và trả lời câu hỏi:
Non sông đã chết, sống thêm nhục,
Hiền thánh còn đâu, học cũng hoài.
Muốn vượt bể Đông theo cánh gió,
Muôn trùng sóng bạc tiễn ra khơi.
(Phan Bội Châu, Lưu biệt khi xuất dương, Ngữ văn 11, tập 2, NXB Giáo dục Việt Nam)
Đâu là cách hiểu đúng về hình ảnh “muôn trùng sóng bạc” trong khổ thơ trên?
Đáp án đúng là: B
Căn cứ vào nội dung đoạn trích.
Dạng bài đọc hiểu tác phẩm văn học
Đáp án cần chọn là: B
Đọc đoạn trích sau đây và trả lời 5 câu hỏi sau:
Đất nước tôi.
Thon thả giọt đàn bầu
Nghe dịu nỗi đau của mẹ
Ba lần tiễn con đi
Hai lần khóc thầm lặng lẽ
Các anh không về, mình mẹ lặng im.
Đất nước tôi,
Từ thuở còn nằm nôi
Sáng chắn bão giông, chiều ngăn nắng lửa
Lao xao trưa hè một giọng ca dao.
Xin hát về Người, đất nước ơi
Xin hát về Mẹ, Tổ quốc ơi
Suốt đời lam lũ
Thương lũy tre làng bãi dâu bến nước
Yêu trọn tình đời muối mặn gừng cay.
(Tạ Hữu Yên, Đất nước, dẫn theo báo Quân đội nhân dân, ngày 27/07/2017)
Trả lời cho các câu 86, 87, 88, 89, 90 dưới đây:
Tác giả KHÔNG xây dựng hình tượng đất nước qua chất liệu nào?
Đáp án đúng là: B
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: B
Trong đoạn thơ trên, đất nước hiện lên như thế nào?
Đáp án đúng là: A
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: A
Phương thức biểu đạt chính của đoạn thơ trên là gì?
Đáp án đúng là: C
Căn cứ vào nội dung của văn bản.
Đáp án cần chọn là: C
Thái độ bao trùm lên đoạn thơ trên là?
Đáp án đúng là: A
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: A
Câu thơ “Ba lần tiễn con đi, hai lần khóc thầm lặng lẽ” cho thấy phẩm chất gì của người mẹ?
Đáp án đúng là: D
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: D
Đọc đoạn trích sau đây và trả lời 5 câu hỏi sau:
Biết bao bạn trẻ bước vào làng văn với quyết định thành một tiểu thuyết gia mà không tự xét có khả năng về loại đó không. Các bạn ấy hãy đọc đoạn tự thú này của Dale Carnegie: “Hồi ba mươi tuổi tôi quyết chuyên viết tiểu thuyết. Tôi sắp thành một Frank Norris hoặc Jack London hoặc T. Hardy thứ nhì. Tôi hăng hải tới nỗi qua ở Châu Âu hai năm. Tại đó tôi sống dễ dàng với vài Mỹ kim mỗi tháng, vì sau đại chiến thế giới thứ nhứt, ở đây có sự lạm phát giấy bạc. Trong hai năm ấy tôi viết một kiệt tác nhan đề là “Blizzard” (Dông tuyết). Nhan đề ấy hợp quả vì bản thảo được các nhà xuất bản đón tiếp một cách lạnh lùng không khác những cơn đông tuyết thổi trên cánh đồng Dakota. Khi nhà xuất bản nói thẳng vào mặt tôi rằng cuốn ấy là đồ bỏ, rằng tôi không tài, không có khiếu về tiểu thuyết thì tim tôi muốn ngừng đập. Tôi quay gót ra như kẻ mất hồn. Có ai đập mạnh vào đầu tôi cũng không làm cho tôi choáng váng hơn. Tôi đê mê, rụng rời.”
Nhưng rồi Dale Carnegie biết quyết định bỏ ngay loại tiểu thuyết để viết tiểu sử các danh nhân cùng loại sách xử thế cho người lớn. Và ông đã thành công rực rỡ, được khắp thế giới biết tên, kiếm được cả triệu Mỹ kim. Ông đã chẳng buồn rầu vì không được là một T.Hardy thứ nhì mà còn muốn nhảy múa mỗi khi nhớ lại quyết định sáng suốt đó. Walter Raleigh nói: “Tôi không có tài để viết một cuốn sách khả dĩ so sánh được với tác phẩm của Shakespeare, nhưng tôi có thể viết một cuốn theo tài năng riêng của tôi được”. Hễ biết theo tài năng riêng của mình thì sẽ vẻ vang, như nữ sĩ De Sévigné chỉ viết những bức thư cho con gái cũng lưu danh thiên cổ, cứ gì phải làm thơ với soạn tiểu thuyết? Có hàng chục con đường dẫn lên ngọn núi vinh hiển; lựa con đường nào hợp với mình mà theo, dù tới muộn, chẳng hơn là theo vết chân người để bị tụt xuống cả trăm lần rồi rốt cuộc, tới già vẫn còn lẹt bẹt ở dưới chân núi ư? Số người có thiên tư về văn thì rất nhiều mà thành công rất ít chính vì phần đông không đủ kiên nhẫn và không biết chọn đường hợp với khả năng của họ vậy.
(Nguyễn Hiến Lê, Nghề viết văn, NXB Nguyễn Hiến Lê, Sài Gòn, 1969)
Trả lời cho các câu 91, 92, 93, 94, 95 dưới đây:
Thao tác lập luận chính trong đoạn trích trên là gì?
Đáp án đúng là: C
Căn cứ vào nội dung đoạn trích
Nội dung/ Thông điệp
Đáp án cần chọn là: C
Biện pháp tu từ nào được sử dụng trong câu văn “Nhan đề ấy hợp quả vì bản thảo được các nhà xuất bản đón tiếp một cách lạnh lùng không khác những cơn dông tuyết thổi trên cánh đồng Dakota"?
Đáp án đúng là: B
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: B
Đâu là thông tin KHÔNG ĐÚNG về Dale Carnegie?
Đáp án đúng là: A
Căn cứ vào nội dung của văn bản.
Đáp án cần chọn là: A
Theo đoạn trích, ít người đạt được thành công về văn chương vì sao?
Đáp án đúng là: C
Căn cứ vào nội dung văn bản, kỉến thức liên quan đến từ láy.
Đáp án cần chọn là: C
Bài học nào được rút ra từ đoạn trích trên?
Đáp án đúng là: A
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: A
Đọc đoạn trích sau đây và trả lời 5 câu hỏi sau:
10.4.68
Vậy là chiều nay các anh lên đường để lại cho mọi người một nỗi nhớ mênh mông giữa khu rừng vắng vẻ. Các anh đi rồi nhưng tất cả nơi đây còn ghi lại bóng dáng các anh: những con đường đi, những chiếc ghế ngồi chơi xinh đẹp, những câu thơ thắm thiết yêu thương. Nghe anh Tuấn ra lệnh: “Tất cả ba lô lên đường!”. Những chiếc ba lô vụng về may bằng những tấm bao Mỹ đã gọn gàng trên vai, mọi người còn nấn ná đứng lại trước mình bắt tay chào mình một lần cuối. Bỗng dưng một nỗi nhớ thương kỳ lạ đối với miền Bắc trào lên trong mình như mặt sông những ngày mưa lũ và... mình khóc ròng đến nỗi không thể đáp lại lời chào của mọi người. Thôi! Các anh đi đi, hẹn một ngày gặp lại lại trên miền Bắc thân yêu
Suốt một đêm một ngày lo lắng vì ca mổ của San, chiều nay lòng mình vui sướng xiết bao khi thấy San ngồi dậy, nét mặt anh còn in nỗi đau đớn mệt nhọc nhưng nụ cười ngượng nở trên môi. Bàn tay anh khẽ nắm bàn tay mình mến thương tin tưởng, người thương binh trẻ tuổi dũng cảm kia ơi, tôi thương anh bằng một tình thương rộng lớn nhưng rất sâu xa: tình thương của một người thầy thuốc trước bệnh nhân, tình thương của một người chị đối với đứa em đau ốm (thực ra San bằng tuổi mình) và tình thương ấy đặc biệt hơn đối với mọi người vì cộng thêm cả lòng mến phục. Anh có thấy điều đó trong cái nhìn lo âu của tôi không? Có thấy bàn tay tôi dịu dàng đặt nhẹ trên vết thương, trên đôi tay xanh gầy của anh đó không? Chúc San mau bình phục để trở về với đội ngũ chiến đấu, trở về với bà mẹ già đang vò võ ngóng trông con từng giờ, từng phút.
(Đặng Thùy Trâm, Nhật kí Đặng Thùy Trâm, NXB Hội Nhà văn, Hà Nội, 2009)
Trả lời cho các câu 96, 97, 98, 99, 100 dưới đây:
Mạch logic gắn kết các phần trong đoạn trích trên là gì?
Đáp án đúng là: B
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: B
Tính phi hư cấu của đoạn trích trên được thể hiện ở yếu tố nào?
Đáp án đúng là: A
Căn cứ nội dung văn bản
Đáp án cần chọn là: A
Biện pháp tu từ được thể hiện trong câu văn “Bỗng dưng một nỗi nhớ thương kỳ lạ đối với miền Bắc trào lên trong mình như mặt sông những ngày mưa lũ và... mình khóc ròng đến nỗi không thể đáp lại lời chào của mọi người” là gì?
Đáp án đúng là: B
Căn cứ vào nội dung của văn bản.
Đáp án cần chọn là: B
Chi tiết Đặng Thùy Trâm nhẹ nhàng đặt tay lên vết thương của thương binh cho thấy điều gì trong phẩm chất của chị?
Đáp án đúng là: A
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: A
Đâu là nhận xét đúng nhất về chủ thể trần thuật trong đoạn trích trên?
Đáp án đúng là: C
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: C