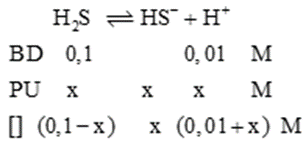Phần 1: Tư duy Toán học
Bánh xe của người đi xe đạp quay được 11 vòng trong 5 giây. Biết rằng đường kính bánh xe đạp là 600mm. Quãng đường mà người đi xe đã đi được trong 30 giây là bao nhiêu mét? (Kết quả làm tròn đến hàng đơn vị).
Đáp án đúng là: 124
- Tính số vòng
- Quãng đường = số vòng.chu vi
Đáp án cần điền là: 124
Huyết áp của mỗi người thay đổi trong ngày. Giả sử huyết áp tâm trương (tức là áp lực máu lên thành động mạch khi tim giãn ra) của một người nào đó ở trạng thái nghỉ ngơi tại thời điểm t được cho bởi công thức: $B(t) = 80 + 7\sin\dfrac{t\pi}{12}$ (mmHg), trong đó t là số giờ tính từ lúc nửa đêm (0 giờ 00 phút) và B(t) tính bằng mmHg (milimét thủy ngân).
Kéo thả đáp án vào các ô trống:
a) Huyết áp tâm trương của người này vào 10 giờ 30 phút sáng là (mmHg)
b) Huyết áp tâm trương của người này vào 12 giờ trưa là (mmHg)
c) Huyết áp của người đó đạt cao nhất tại thời điểm sớm nhất trong ngày là lúc (giờ)
Đáp án đúng là: 82,68; 80; 6
a) Thay t = 10,5
b) Thay t = 12
c) Đánh giá B(t)
Đáp án cần chọn là: 82,68; 80; 6
Cho hàm số $y = \cos x + \sin x$
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
| Đúng | Sai | |
|---|---|---|
| a) Hàm số đã cho tuần hoàn với chu kì $T = \dfrac{\pi}{2}$ | ||
| b) Hàm số đã cho là hàm số chẵn | ||
| c) Số điểm biểu diễn của phương trình $y = \dfrac{\sqrt{2}}{2}$ trên đường tròn lượng giác là 1 |
Đáp án đúng là: S; S; S
Xét từng đáp án
Tìm chu kì của hàm số lượng giác
Đáp án cần chọn là: S; S; S
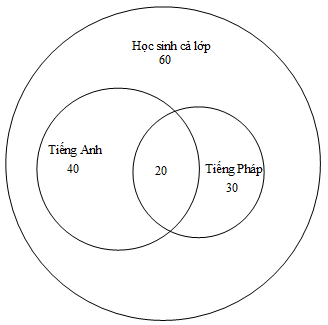
Một lớp học trong một trường đại học có 60 sinh viên, trong đó có 40 sinh viên học tiếng Anh, 30 sinh viên học tiếng Pháp và 20 sinh viên học cả tiếng Anh và tiếng Pháp. Chọn ngẫu nhiên 2 sinh viên của lớp học này. Tính xác suất để 2 sinh viên được chọn không học ngoại ngữ. Biết rằng trường này chỉ dạy hai loại ngoại ngữ là tiếng Anh và tiếng Pháp.
Đáp án đúng là: B
Đáp án cần chọn là: B
Sau khoảng thời gian từ 0 giờ đến 3 giờ thì kim giây đồng hồ sẽ quay được một góc có số đo bằng:
Đáp án đúng là: D
- Tính số đo trong 1 phút.
- Tính số đo trong 3 giờ.
Đáp án cần chọn là: D
Có bao nhiêu số nguyên m để phương trình $\sin 3x = \sqrt{2m - 1} + 1$ có nghiệm?
Đáp án đúng là: D
- Biện luận m
Đáp án cần chọn là: D
Phương trình $\sin 2x = m^{2} - 2m + 2$ có tối đa bao nhiêu nghiệm trên khoảng $\left( {0;2\pi} \right)$?
Đáp án đúng là: B
Tìm điều kiện để phương trình có nghiệm => sinx ≤ 1
Đáp án cần chọn là: B
Cho hàm số $y = f(x) = a\sin\left( {bx + c} \right),\,\,(a,b,c \in {\mathbb{R}})$ có đồ thị như hình vẽ.
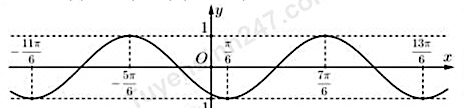
Điền đáp án vào các ô trống sau:
a) Chu kì của hàm số là T = kπ. Giá trị của k là:
b) Giá trị của $|b|$ là
Đáp án đúng là: 2; 1
a) Quan sát đồ thị tìm chu kì.
b) Hàm số $y = k.\sin(ax + b),y = k.\cos(ax + b)$ tuần hoàn với chu kỳ $T = \dfrac{2\pi}{|a|}$.
Đáp án cần điền là: 2; 1
Cho tam giác ABC như hình vẽ.

Phép vị tự tâm A tỉ số $k = \dfrac{3}{2}$ biến tam giác ABC thành tam giác A′B′C′. Khi đó, diện tích tam giác A′B′C′ bằng ________ ô vuông.
Đáp án đúng là: A
Đáp án cần chọn là: A
Gọi $S$ là tập hợp tất cả các giá trị thực của tham số $m$ để giá trị nhỏ nhất của hàm số $y = f(x) = 4x^{2} - 4mx + m^{2} - 2m$ trên đoạn $\lbrack - 2;0\rbrack$ bằng 3 . Tính tổng $T$ các phần tử của $S$.
Đáp án đúng là: D
Đáp án cần chọn là: D
Cho số thực $a$ và hàm số $f(x) = \begin{cases} {2x} & {\text{khi}x \leq 1} \\ {a\left( {x - 2x^{2}} \right)} & {\text{khi}x > 1} \end{cases}$ liên tục trên $\mathbb{R}$. Tính ${\int_{0}^{2}f}(x)\text{dx}$.
Đáp án đúng là: C
Đáp án cần chọn là: C
Biết khai triển $\left( {1 + 2x + 3x^{2}} \right)^{10} = a_{0} + a_{1}x + a_{2}x^{2} + \ldots + a_{20}x^{20}$. Tính tổng $S = a_{0} + 2a_{1} + 4a_{2} + \ldots + 2^{20}a_{20}$.
Đáp án đúng là: B
Đáp án cần chọn là: B
Cho tập hợp A = {1,2,3,4,.,20}. Chọn ngẫu nhiên 3 số trong tập hợp A. Tính xác suất để ba số được chọn không có 2 số tự nhiên liên tiếp.
Đáp án đúng là: A
Số cách chọn ba số đôi một khác nhau từ A: $n(\Omega) = C_{20}^{3}$.
TH1: Ta chọn số có 3 chữ số tự nhiên liên tiếp
TH2: Chọn ba số có đúng hai chữ số liên tiếp
Đáp án cần chọn là: A
Trong 1 cái hộp có 3 bi đỏ, 4 bi vàng, 5 bi xanh cùng chất, cùng kích thước. Một người lấy ngẫu nhiên cùng lúc 4 viên bi. Tính xác suất để số bi đỏ mà người đó lấy được không lớn hơn 2.
Đáp án đúng là: C
Gọi A: “Biến cố trong 4 bi lẫy ngẫu nhiên có 3 bi màu đỏ”.
Tính $1 - P(A)$
Đáp án cần chọn là: C
a) Mật khẩu của chương trình máy tính quy định gồm 3 kí tự, mỗi kí tự là một chữ số. Khi đó có thể tạo được mật khẩu khác nhau
b) Nếu chương trình máy tính quy định mới mật khẩu vẫn gồm 3 kí tự, nhưng kí tự đầu tiên phải là một chữ cái in hoa trong bảng chữ cái tiếng Anh gồm 26 chữ (từ A đến Z) và 2 kí tự sau là các chữ số (từ 0 đến 9). Khi đó quy định mới có thể tạo được nhiều hơn quy định cũ mật khẩu khác nhau
Đáp án đúng là: 1000; 1600
a) Giả sử mật khẩu của máy tính gồm 3 ký tự, mỗi ký tự là một chữ số. Sử dụng quy tắc nhân.
b) Giả sử mật khẩu mới của máy tính gồm 3 ký tự , ký tự đầu là một chữ cái in hoa, 2 ký tự sau là một chữ số.
Chọn ký tự đầu tiên là một chữ cái in hoa trong bảng chữ cái tiếng Anh.
Chọn ký tự thứ hai là các chữ số (từ 0 đến 9)
Chọn ký tự thứ ba là các chữ số (từ 0 đến 9)
Đáp án cần chọn là: 1000; 1600
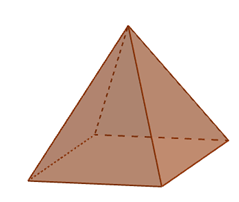
Kim tự tháp Cheops (có dạng hình chóp) là kim tự tháp cao nhất ở Ai Cập. Chiều cao của kim tự tháp này là 144 m, đáy của kim tự tháp là hình vuông có cạnh dài 230 m. Các lối đi và phòng bên trong chiếm 30% thể tích của kim tự tháp. Để xây dựng kim tự tháp, người Ai Cập cổ đại đã vận chuyển các khối đá qua những lối đi vào phòng bên trong. Biết một lần vận chuyển gồm 10 xe, mỗi xe chở 6 tấn đá, và khối lượng riêng của đá bằng 2,5.103 kg/m3. Số lần vận chuyển đá để xây dựng kim tự tháp là:
Đáp án đúng là: 74060
Tính thể tích kim tự tháp để tính thể tích khối đá từ đó tính số lần vận chuyển.
Đáp án cần điền là: 74060
Giá trị của n ∈ N* thỏa mãn đẳng thức $C_{n}^{6} + 3C_{n}^{7} + 3C_{n}^{8} + C_{n}^{9} = 2C_{n + 2}^{8}$ là
Đáp án đúng là: C
Sử dụng máy tính để chọn đáp số đúng:
Đáp án cần chọn là: C
Cho khai triển $\left( {\dfrac{1}{\sqrt{2}} + 3} \right)^{n}.$
Khẳng định nào đúng trong các khẳng định sau?
Đáp án đúng là: A; C
Xét từng mệnh đề.
Đáp án cần chọn là: A; C
Để trang trí cho quán trà sữa sắp mở cửa của mình, bạn Việt quyết định tô màu một mảng tường hình vuông cạnh bằng 1 m. Phần tô màu dự kiến là các hình vuông nhỏ được đánh số lần lượt là 1,2,3…n,…, trong đó cạnh của hình vuông kế tiếp bằng một nửa cạnh hình vuông trước đó như hình vẽ. Giả sử quá trình tô màu của Việt có thể diễn ra nhiều giờ. Hỏi bạn Việt tô màu đến hình vuông thứ mấy thì diện tích của hình vuông được tô bắt đầu nhỏ hơn $\dfrac{1}{1000}\left( m^{2} \right)$?
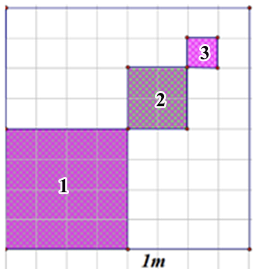
Đáp án đúng là: C
Đáp án cần chọn là: C
Cho cấp số cộng (un) có u1 = 3 và công sai d = 2, và cấp số cộng (vn) có v1 = 2 và công sai d′ = 3. Gọi X, Y là tập hợp chứa 1000 số hạng đầu tiên của mỗi cấp số cộng. Chọn ngẫu nhiên 2 phần tử bất kỳ trong tập hợp X ∪ Y. Xác suất để chọn được 2 phần tử bằng nhau gần với số nào nhất trong các số dưới đây?
Đáp án đúng là: C
Đáp án cần chọn là: C
Cho tứ giác ABCD. Trên các cạnh AB, BC, CD, AD lần lượt lấy 3; 4; 5; 6 điểm phân biệt khác các điểm A, B, C, D. Số tam giác phân biệt có các đỉnh là các điểm vừa lấy là
Đáp án đúng là: D
Đáp án cần chọn là: D
Cho các số dương a, b, c thỏa mãn $a \neq 1,\,\,\log_{3}a + b = 0,\,\,\log_{a}b = \dfrac{1}{c},\,\,\ln\dfrac{b}{c} = c - b$. Tổng $S = a + b + c$ nằm trong khoảng nào cho dưới đây?
Đáp án đúng là: B
Đáp án cần chọn là: B
Kéo số ở các ô vuông thả vào vị trí thích hợp:
Một xe dịch vụ chất lượng cao đi từ Hà Giang xuống Hà Nội chở được nhiều nhất 50 hành khách trên một chuyến đi. Theo tính toán của nhà xe, nếu xe chở được k khách thì giá tiền mà mỗi khách phải trả khi đi tuyến đường này là $\left( {180 - \dfrac{3k}{2}} \right)^{2}$ trăm đồng. Tổng số tiền thu được từ hành khách nhiều nhất là nghìn đồng khi xe chở hành khách.
Đáp án đúng là: 576000; 40
Đáp án cần chọn là: 576000; 40
Trong các hàm số sau, hàm số nào không tồn tại giới hạn khi x→0
Đáp án đúng là: B; C; D
- Sử dụng phương pháp loại trừ.
Đáp án cần chọn là: B; C; D
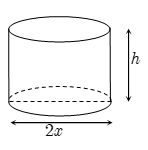
Công ty X muốn thiết kế các hộp chứa sản phẩm dạng hình trụ có nắp với dung tích bằng 330 cm3, bán kính đáy x cm, chiều cao ℎ cm. Khi thiết kế, công ty X luôn đặt mục tiêu sao cho vật liệu làm vỏ hộp là ít nhất, nghĩa là diện tích toàn phần hình trụ là nhỏ nhất.
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau :
Để công ty X tiết kiệm được vật liệu nhất thì bán kính x bằng cm và chiều cao ℎ bằng cm.
(Kết quả làm tròn đến chữ số thập phân thứ ba).
Đáp án đúng là: 3,745; 7,490
Đáp án cần chọn là: 3,745; 7,490
Cho các số thực $a,b,c \in (1; + \infty)$ thỏa mãn $a^{10} \leq b$ và $\log_{a}b + 2\log_{b}c + 5\log_{c}a = 12$. Giá trị nhỏ nhất của biểu thức $P = 2\log_{a}c + 5\log_{c}b + 10\log_{b}a$ bằng
Đáp án đúng là: B
Đáp án cần chọn là: B
Cho dãy số $\left( u_{n} \right)$ được xác định bởi $\left\{ \begin{matrix} {u_{1} = 1,u_{2} = 3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} \\ {u_{n + 2} + u_{n} = 2\left( {u_{n + 1} + 1} \right),\,\,\, n \in {\mathbb{N}}^{*}} \end{matrix} \right.$. Giới hạn $\lim\limits_{n\rightarrow + \infty}\dfrac{u_{n}}{n^{2}}$ bằng ________.
Đáp án đúng là: 1
Đáp án cần điền là: 1
Cho $\lim\limits_{x\rightarrow 3}\dfrac{x - 3}{x^{2} + ax + b - 2} = \dfrac{1}{7}$ với a ,b là các số hữu tỉ. Tính $P = a - 3b$
Đáp án đúng là: B
Đáp án cần chọn là: B
Cho hàm số $f(x) = \dfrac{\sqrt{1 + mx} - \sqrt{1 + mx^{2}}}{5x}$. Tìm giá trị thực của tham số m để hàm số $f(x)$ có giới hạn bằng 1 khi x dần tới 0
Đáp án đúng là: A
Đáp án cần chọn là: A
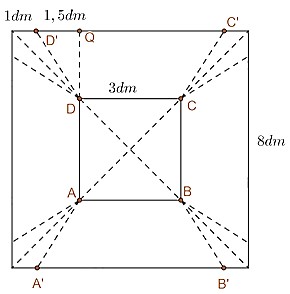
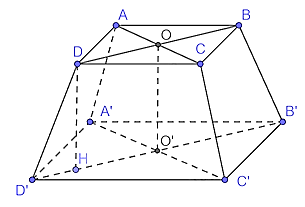
Từ một tấm tôn hình vuông có cạnh 8 dm, bạn Hùng cắt bỏ bốn phần như nhau ở bốn góc, sau đó bác hàn các mép lại để được một chiếc thùng (không nắp) như hình bên dưới
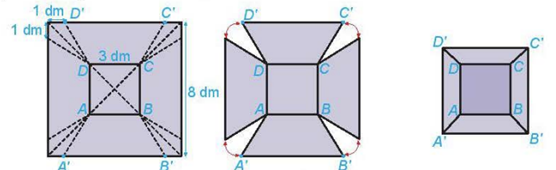
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
| Đúng | Sai | |
|---|---|---|
| a) Chiếc thùng nhận được là hình chóp cụt | ||
| b) Cạnh bên của chiếc thùng là 3 dm | ||
| c) Thùng có thể chứa được nhiều nhất 42 lít nước |
Đáp án đúng là: Đ; S; Đ
b) Cạnh bên của chiếc thùng là độ dài cạnh DD’
Kẻ DQ vuông góc với D’C’
c) Số lít nước mà thùng có thể chứa được nhiều nhất bằng thể tích của hình chóp cụt.
Gọi O và O’ lần lượt là tâm của ABCD và A’B’C’D’
Qua D kẻ DH vuông góc với O’D’
Đáy A’B’C’D’ có cạnh là 6dm
Tính:
O′D′
OD
Đáp án cần chọn là: Đ; S; Đ
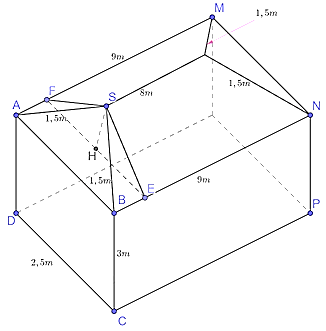
Cho ngôi nhà 4 mái dốc có kích thước như sau
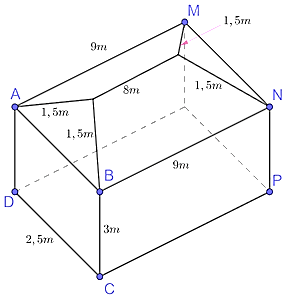
Điền số thích hợp vào ô trống (Làm tròn đến chữ số thập phân thứ hai)
Chiều cao từ đỉnh cao nhất của ngôi nhà đến mặt đất là ___________ m
Đáp án đúng là: 3,66
Chiều cao từ đỉnh cao nhất của ngôi nhà đến mặt đất là khoảng cách từ S đến mặt đất.
Gọi H là hình chiếu của S lên (ABNM).
Khi đó khoảng cách từ S đến mặt đất bằng tổng độ dài SH và độ dài BC.
Qua H kẻ (α) vuông góc với (ABNM), cắt BN, AM lần lượt tại E và F.
Đáp án cần điền là: 3,66
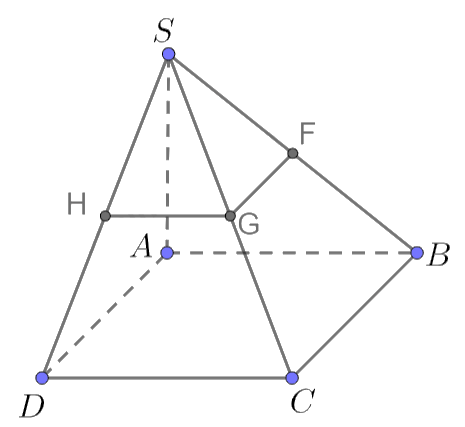
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, $SA\bot(ABCD)$ và $SA = a$. Gọi F, G, H lần lượt là trung điểm của SB, SC, SD. Tính khoảng cách giữa AF và GH.
Đáp án đúng là: B
Phương pháp tính khoảng cách giữa hai đường thẳng
Đáp án cần chọn là: B
Cho lăng trụ đứng tam giác như hình vẽ
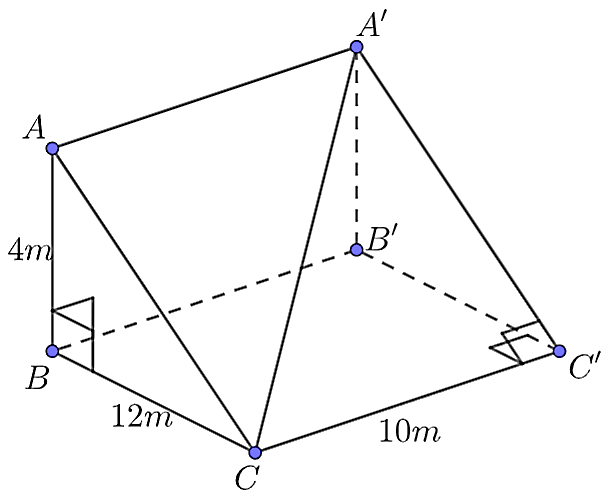
Giá trị tan góc giữa đường thẳng CA′ và (CC′B′B) là
Đáp án đúng là: D
Đáp án cần chọn là: D
Góc nhị diện [P,d,Q]
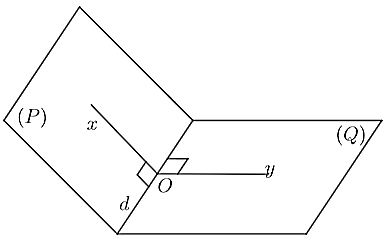
Hình gồm hai nửa mặt phẳng (P) và (Q) có chung bờ d được gọi là một góc nhị diện, kí hiệu [P,d,Q]. Từ một điểm O thuộc d, kẻ các tia Ox, Oy lần lượt thuộc hai nửa mặt phẳng (P) và (Q) và cùng vuông góc với d. Góc xOy được gọi là góc phẳng nhị diện của [P,d,Q]. Số đo của xOy được gọi là số đo của góc [P,d,Q].
Gọi A, B lần lượt là 2 điểm thuộc (P) và (Q) (A,B ∉ d). Khi đó ta coi [A,d,B] như là góc nhị diện [P,d,Q]. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, AB = a, SA ⊥ (ABC), SA = $a\sqrt{3}$.
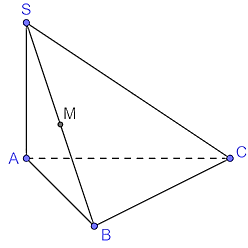
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
| Đúng | Sai | |
|---|---|---|
| a) Góc nhị diện [B,SA,C] là góc $\widehat{BSC}$ | ||
| b) Góc [B,SA,C] có số đo 450 | ||
| c) Gọi M là trung điểm của SB. Giá trị tan của góc [M,BC,A] là $\sqrt{3}$ |
Đáp án đúng là: S; Đ; Đ
Đọc kĩ giả thiết và xét từng mệnh đề.
Đáp án cần chọn là: S; Đ; Đ
Cho tứ diện $\text{ABCD}$. Lấy các điểm $\text{M}$ và $\text{N}$ lần lượt thuộc $\text{AD}$ và $\text{BC}$ sao cho $\overset{\rightarrow}{AM} = 3\overset{\rightarrow}{MD}$, $\overset{\rightarrow}{NB} = - 3\overset{\rightarrow}{NC}$. Biết $\overset{\rightarrow}{AB} = \overset{\rightarrow}{a},\overset{\rightarrow}{CD} = \overset{\rightarrow}{b}$. Biết $\overset{\rightarrow}{MN} = x\overset{\rightarrow}{a} - y\overset{\rightarrow}{b}$.
Khi đó x + y = __________
Đáp án đúng là: 1
Đáp án cần điền là: 1
Viết liền nhau các số tự nhiên từ 1 đến 100. Khi đó chữ số 5 được viết bao nhiêu lần?
Đáp án đúng là: B
Đáp án cần chọn là: B
Hàm Euler của một số nguyên dương N được định nghĩa là số các số nguyên dương nhỏ hơn hoặc bằng N và nguyên tố cùng nhau với N, kì hiệu là ϕ(N). Hai số nguyên dương a và b được gọi là nguyên tố cùng nhau nếu ƯCLN(a,b)=1.
Chọn các khẳng định đúng:
Đáp án đúng là: A; C
Tìm các số nguyên nhỏ hơn hoặc bằng n và nguyên tố cùng nhau với n.
Đáp án cần chọn là: A; C
Cho n là số tự nhiên nhỏ nhất khi chia cho 7, 5, 3, 11 có cùng số dư là 1.
Khi đó n = __________
Đáp án đúng là: 1156
Đưa về (n − 1)
Đáp án cần điền là: 1156
Cho các số thực dương a, b, c thỏa mãn $a^{\log_{3}7} = 27,\,\, b^{\log_{7}11} = 49,\,\, c^{\log_{11}25} = \sqrt{11}\text{.~}$
Mỗi phát biểu sau đây là đúng hay sai?
| Đúng | Sai | |
|---|---|---|
| a) $\sqrt[3]{a^{{({\log_{3}7})}^{2}}} = 14$ | ||
| b) $c^{{({\log_{11}25})}^{2}} = 5$ | ||
| c) $\sqrt[3]{a^{{({\log_{3}7})}^{2}}} + \sqrt{b^{{({\log_{7}11})}^{2}}} + c^{{({\log_{11}25})}^{2}} = 23$ |
Đáp án đúng là: S; Đ; Đ
Đáp án cần chọn là: S; Đ; Đ
Cho $- 5 \leq a \leq 5$ . Giá trị của $\sum\limits_{a = - 5}^{5}\left\lbrack \dfrac{a}{3} \right\rbrack$ là:
Đáp án đúng là: B
Đáp án cần chọn là: B
Phần 2: Tư duy đọc hiểu
Đọc ngữ liệu sau và trả lời các câu hỏi:
DỊCH BỆNH CÂY TRỒNG
[0] Cũng giống như nhiều người trong chúng ta phải đối diện với cúm mùa, các cây trồng bản địa phải đối mặt với các mối đe dọa từ virus. Con người từ lâu đã biết rằng giống như con người, cây trồng có thể không kháng cự nổi các loại virus.
[1] Hiện tại một nghiên cứu do các nhà khoa học trường đại học bang Michigan và trường đại học California, Riverside cho thấy một đe dọa chưa từng biết từ trước đến nay: các virus trên cây trồng phi bản địa đang ảnh hưởng và gây nguy hiểm đến sức khỏe của cây dại sa mạc.
[2] “Trong nhiều năm, lĩnh vực sinh thái học giả định là cây dại đã miễn dịch với các virus xâm lấn phá hủy mùa vụ”, Carolyn Malmstrom, giáo sư sinh học thực vật, sinh học tiến hóa và hành vi tại MSU và đồng dẫn dắt nghiên cứu nhận xét. Kerry Mauck, một phó giáo sư và giữ ghế Alfred M. Boyce về côn trùng học, là người dẫn dắt nhóm nghiên cứu tại UC Riverside và cố vấn cho tác giả thứ nhất Tessa Shates, một sinh viên trong phòng thí nghiệm của mình. “Nhưng chúng tôi phát hiện ra là chúng ta cần phải lo nghĩ nhiều về việc bảo vệ những cây cối bản địa cũng giống như việc chúng ta lo nghĩ về cây nông nghiệp”, Malmstrom nói.
[3] Được xuất bản trên tạp chí Phytobiomes Journal, phát hiện này có những gợi ý đáng chú ý cho những nỗ lực bảo tồn. Nghiên cứu sử dụng kỹ thuật giải trình tự gene tiên tiến và thực nghiệm ngoài hiện trường để chứng tỏ cách các côn trùng, đóng vai trò như những vật truyền lây không chủ ý, chuyên chở các mầm bệnh gây hại từ nơi trồng trọt sang các hệ sinh thái bản địa.
[4] Nghiên cứu này tập trung vào những vùng sa mạc ở Nam California, nơi các loài bí hoang Cucurbita mọc gần với các cánh đồng canh tác được tưới tiêu. Nhóm nghiên cứu đã nhận diện, đánh dấu và thu thập các mẫu từ cây dại một cách cẩn thận. Sau đó, phân tích gene của các loài virus bên trong những mẫu cây dại này, các nhà nghiên cứu đã khám phá ra một sự hiện diện đáng ngạc nhiên của các mầm bệnh của cây trồng như virus gây bệnh còi cọc vàng ở dưa chuột và virus vàng dưa chuột do rệp sinh ra, hay bệnh CABYV.
[5] Trên thực tế, họ cũng tìm thấy tỉ lệ lây nhiễm với CABYV – một mầm bệnh phi bản địa – có thể đạt đến mức cao tới 88% trên quần thể Cucurbita dại, với những tác động hữu hình lên sự tăng trưởng của cây trồng và sức khỏe của rễ, cả về sự tồn tại của cây trồng trong môi trường sa mạc khắc nghiệt. “Các cây dại này là thành phần quan trọng của các hệ sinh thái sa mạc, đem lại thức ăn và nơi trú ngụ của các sinh vật khác”, Malmstrom nói. “Sự suy giảm của chúng do nhiễm virus từ cây trồng có thể dẫn đến những hệ quả chồng chất đối với toàn bộ các cộng đồng sinh thái”.
[6] “Phát hiện của chúng tôi giúp cộng đồng ghi nhận một điều là tác động của chúng ta lên quang cảnh xung quanh chúng ta không bao giờ được nhìn thấy rõ ràng hoặc rõ ràng để thấy được”, Shates nói. “Thật dễ để thấy những thay đổi cảnh quan của một khu rừng bị đốn hạ nhưng khó hơn nhiều để ghi nhận cách các vi sinh vật quá giang có thể làm thay đổi cấu trúc cộng đồng thực vật theo thời gian”.
[7] “Dự án này bắc cầu qua khoảng trống giữa các hệ nông nghiệp và tự nhiên, nhắc nhở chúng ta là tự nhiên và nông nghiệp đều có mối liên hệ chặt chẽ”, Malmstrom nói. “Nó cũng nhấn mạnh vào sự cần thiết có cách tiếp cận tối ưu hơn để quản lý sức khỏe cây trồng và chứng tỏ hiểu biết về động lực học virus đầy phức tạp trong các hệ tự nhiên là điều thiết yếu để phát triển các giải pháp bền vững giúp đem lại lợi ích cho cả nông nghiệp và đa dạng sinh học”.
(Thanh Đức tổng hợp, tiasang.com.vn, ngày 02/04/2024)
Trả lời cho các câu 41, 42, 43, 44, 45, 46, 47, 48, 49, 50 dưới đây:
Hoàn thành câu bằng cách chọn đáp án Đúng hoặc Sai:
Cây trồng bản địa không thể kháng cự các loại virus.
Đúng hay Sai?
Đáp án đúng là: B
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Đáp án cần chọn là: B
Theo đoạn [2], nhà nghiên cứu Carolyn Malmstrom và Kerry Mauck đã nhận định điều gì về sự miễn dịch của cây dại đối với virus?
Đáp án đúng là: C
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Đáp án cần chọn là: C
Chọn từ thích hợp để điền vào chỗ trống trong câu:
Văn bản trên được viết theo phong cách ngôn ngữ _____________.
Đáp án đúng là: D
Tìm từ khóa chính, vận dụng kiến thức về phong cách ngôn ngữ.
Đáp án cần chọn là: D
Điền một cụm từ không quá ba tiếng có trong đoạn [6] vào chỗ trống để hoàn thành câu:
của chúng ta lên quang cảnh xung quanh không bao giờ được nhìn thấy rõ ràng, nhưng những thay đổi cảnh quan của một khu rừng bị đốn hạ có thể dễ dàng được nhận biết.
Đáp án đúng là: Tác động
Tìm từ khóa chính, căn cứ logic câu từ, đối chiếu với ngữ liệu.
Đáp án cần điền là: Tác động
Ý chính của bài viết viết là gì?
Đáp án đúng là: D
Đọc hiểu nội dung toàn bài, suy ra ý chính của bài viết.
Đáp án cần chọn là: D
Loài cây gì được nghiên cứu trong vùng sa mạc Nam California?
Đáp án đúng là: C
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Đáp án cần chọn là: C
Hoàn thành câu bằng cách chọn đáp án Đúng hoặc Sai:
Phát hiện trong nghiên cứu tập trung vào vùng sa mạc Nam California.
Đúng hay Sai?
Đáp án đúng là: A
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Đáp án cần chọn là: A
Hoàn thành câu bằng cách chọn đáp án Đúng hoặc Sai:
Nghiên cứu đã chỉ ra rằng cây dại không bị ảnh hưởng bởi virus.
Đúng hay Sai?
Đáp án đúng là: B
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Đáp án cần chọn là: B
Hoàn thành các câu sau bằng cách kéo thả các cụm từ vào đúng vị trí:
1. Nghiên cứu do nhóm tại trường đại học Michigan và trường đại học California, Riverside thực hiện.
2. Nghiên cứu đã ra các mầm bệnh virus đe dọa đến sức khỏe của cây dại, đặc biệt là các loại virus gây hại như virus còi cọc vàng ở dưa chuột và virus vàng dưa chuột do rệp sinh ra.
3. Bài viết nhấn mạnh vào sự quan trọng của việc bảo vệ cây dại và cảnh báo về tác động tiềm ẩn của con người đối với .
Đáp án đúng là: nhà khoa học; phát hiện; môi trường
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Đáp án cần chọn là: nhà khoa học; phát hiện; môi trường
Phương pháp nào đã được sử dụng trong nghiên cứu để thu thập mẫu cây dại?
Đáp án đúng là: C
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Đáp án cần chọn là: C
Đọc ngữ liệu sau và trả lời các câu hỏi:
BÓNG NGƯỜI TRÊN SƯƠNG MÙ
[0] Ở ngoài, đêm tối như mực. Trong toa hạng nhì, riêng tôi ngồi đối diện với Trạch, một người bạn cũ, tình cờ gặp vì cùng đi một chuyến xe. Mười năm trước, bạn tôi còn là một người cầm lái xe lửa, cũng hàn vi như tôi; bây giờ gặp lại nhau trong toa hạng nhì, hai người cùng ngạc nhiên và cùng mừng cho nhau.
[1] Lúc nói chuyện, tôi thấy bên cạnh bạn có cái hộp khảm rất đẹp liền cầm lấy xem, rồi tình cờ mở hộp ra; bạn tôi như có ý không bằng lòng, nhưng vì nể tôi nên không nói gì. Tôi nhìn vào hộp thấy rất lạ: hộp bịt kính, ở trong có một con bướm rất to, hai cánh đã xơ xác. [...]
Thấy bạn có vẻ khác, tôi đoán có chuyện gì, liền hỏi:
- Con bướm này chắc cũng có sự tích gì đây?
- Vâng, nhưng sự tích buồn... chuyện đã ngoài mười năm: mười năm trước độ anh đi Sài Gòn thì tôi còn là anh cầm lái tầu hỏa. Chính độ ấy tôi chạy con đường này, tình cảnh tôi độ ấy anh đã rõ.
- Cũng như tình cảnh tôi...
- Nhưng có một việc tôi không nói anh hay, là độ ấy tôi có lấy một người vợ, nhưng giấu nhà, giấu mọi người, giấu anh. Chúng tôi sống trong cảnh nghèo khổ mà thật lấy làm sung sướng. Nhưng vì cảnh nghèo, vì nhà tôi không quen chịu được kham khổ nên người một ngày một yếu dần.
[2] Về sau nhà tôi bị bệnh nặng mà tôi thì vẫn phải đi làm, không ai trông nom ở nhà. Một đêm nhà tôi yếu quá ngất người đi mấy lần, mà chính đêm ấy là đêm tôi được ông Chánh cử đi cầm lái chuyến xe riêng chở quan Toàn quyền. Thật là một dịp rất hay cho tôi. Nhưng tôi biết không thể nào đi được, liền vào kêu với ông Chánh, nói là vợ ốm. Ông Chánh đập bàn, đập ghế, gắt:
- Tôi không biết! Một là mười giờ đêm nay anh phải có mặt ở ga, hai là từ giờ này trở đi, anh đừng bước chân đến đây nữa. Thôi anh ra đi.
Lời ông Chánh nói quả quyết, tôi phân vân không biết nghĩ ra sao: lúc về nhà, ngồi ở đầu giường, nhìn đến vợ mới biết rằng không đi được, dầu có mất việc làm cũng không cần.
Nhà tôi thấy tôi có vẻ lo nghĩ, hỏi duyên cớ vì sao, tôi liền đem việc ấy kể cho nhà tôi nghe. Nhà tôi nghe xong, vẻ mặt tươi hẳn lên, bảo tôi rằng:
- Thế cậu đi chứ! Việc gì phải ngần ngừ! Tôi không việc gì đâu, đã thấy đỡ nhiều. Chiều mai về mua cái gì làm quà cho tôi đấy.
[3] Tôi thấy nhà tôi cười, nói vui vẻ, tôi vững tâm, thay quần áo ra ga. Đến ga đúng mười giờ. Nhưng khi cho xe chạy rồi, tôi mới thấy lo, tôi mới biết là tôi liều. Lúc đó, tôi có cái cảm giác lạ lắm: hình như tôi đi thế này, lúc về chắc không nhìn thấy mặt vợ nữa. Tôi cố định trí để cầm máy, nhưng chỉ được một lúc thôi.
Bỗng cả chuyến xe lửa nghiêng về một bên, rồi lắc lư như muốn đổ. Người "ét" của tôi, vội bỏ cái xẻng xúc than, níu lấy tôi nói:
- Ô hay! Hôm nay ông làm sao thế? Chỗ ấy đường cong nguy hiểm thế mà ông không hãm máy. Ông ngủ à?
Tôi không ngủ nhưng người tuy ở đây mà trí còn nghĩ đến người vợ nằm đợi chết một thân, một mình trong gian nhà nhỏ kia. Mắt tôi hoa lên, mồ hôi ra ướt đẫm cả người.
[4] Xe đi vào khe núi, hết lên cao lại xuống thấp như có vẻ nhọc nhằn. Tôi thò đầu ra cửa, nhìn thẳng trước mặt, nhưng đêm ấy sương mù đầy trời, không nhìn rõ gì cả, chỉ một mầu trắng xóa dưới ánh hai cái đèn ở đầu toa. Bỗng tôi thấy... rõ ràng tôi thấy in trên sương mù một cái hình người đàn bà mặc áo rộng đứng dang tay. Tôi dụi mắt tưởng mình trông hoảng, nhưng không, hình người đàn bà vẫn đấy. Tôi gọi người "ét" lại cửa toa, bảo anh ta nhìn rồi hỏi:
- Bác có thấy gì không?
Vừa nói xong hình người vụt biến mất. Bác "ét" thò đầu ra và bảo tôi:
- Chỉ thấy sương mù! Ông lại mê ngủ rồi.
- Không, rõ ràng tôi thấy có hình người đàn bà in trên sương mù nhưng vừa biến mất. [...]
[5] Còn tôi lúc bấy giờ hai tai ù như người mất trí khôn: tôi văng vẳng nghe có tiếng người ở thật xa đưa lại, tiếng một người đàn bà bảo tôi:
- Đỗ lại, đỗ lại!
Tôi lắng tai, tay nắm chặt lấy cái "phanh" như định hãm rồi lại không dám hãm.
Một lát, tôi lại nghe thấy tiếng người đàn bà, rõ hơn lần trước, giục tôi:
- Hãm lại, hãm lại ngay!
Lúc bấy giờ tôi không biết gì nữa, nhắm mắt hãm phanh lại thật mạnh. Các toa rùng một cái, bánh xe kêu rít lên trong đêm thanh vắng. Xe chạy từ từ một quãng rồi đỗ hẳn. Tôi chưa kịp bước xuống, đã thấy người "xếp tanh" cầm đèn chạy lên hỏi:
- Việc gì thế?
Tôi luống cuống không biết trả lời làm sao, vì nói thật ai tin mình. Tôi trả lời một cách mập mờ:
- Chắc có sự gì lạ. Để tôi cầm đèn đi xem đã.
[6] Lúc bấy giờ mấy ông quan hầu quan Toàn quyền cũng vừa đến, rồi thấy lạ, đi theo chúng tôi. Vừa đi được một quãng thì nghe trước mặt có tiếng nước chảy ầm ầm. Tôi định tâm mới nhớ ra rằng đó là cầu N.G.
Mấy đêm ấy mưa lũ, nước chắc chảy xiết, nên mới réo to như vậy. Đến bờ sông, giơ đèn lên soi, mấy người đều kinh hoảng: cái cầu N.G. bị nước nguồn chảy về xoáy gẫy làm đôi.
Một ít nữa, nếu không hãm kịp thì cả một chuyến xe riêng chở quan Toàn quyền đâm nhào xuống sông sâu, chắc không sống sót một ai; tưởng không có cái tai nạn nào ghê gớm hơn, thế mà chính vì tôi nên mới không có cái tai nạn ấy. Tôi đứng ngẩn người, không hiểu ra sao cả. [...]
[7] Tôi chắc rồi sau thế nào cũng được trọng thưởng, nhưng trọng thưởng lúc đó đối với tôi cũng như không, tôi chỉ nghĩ đến nhà tôi ở nhà, không biết ra sao. Tôi đi trở lại và thoáng thấy con gì bám ở cái đèn để đầu toa. Nhìn kỹ thì ra là một con bướm thật to, vướng vào đèn, đương đập cánh để tìm đường thoát. Chính là con bướm trong cái hộp này đây.
Trông thấy con bướm tôi thốt nghĩ ra ngay. Chính phải rồi, chính cái hình người đàn bà lúc nãy là cái bóng con bướm này in lên trên sương mù, đầu con bướm là đầu hình người, mà hai cánh con bướm đập là hai cái tay người vẫy.
Tôi bắt con bướm rồi định thả cho nó bay đi; sau nghĩ con bướm đã giúp mình được việc, nên giữ lại làm kỷ niệm. Tôi nhìn vào đồng hồ trong toa, thấy kim chỉ đúng hai giờ đêm...
[8] Hôm sau tôi vừa về tới cổng nhà thì thằng nhỏ chạy ra báo tin nhà tôi mất, mất vào quãng một giờ đêm hôm qua.
Tôi không hay tin nhảm; tôi chắc đó chỉ là một sự tình cờ, một sự ngẫu nhiên, nhưng tôi vẫn yên trí rằng linh hồn nhà tôi đã nhập vào con bướm này để phù hộ cho tôi tránh được cái tai nạn đêm hôm ấy. Nhưng tránh được cái tai nạn mà làm gì, tôi thoát được thân tôi mà làm gì, giầu sang phú quý bây giờ đối với tôi như không, tôi cũng chỉ như con bướm này, xác đấy mà hồn tận đâu đâu...
Bạn tôi kể xong câu chuyện, đậy cái hộp khảm lại rồi thẫn thờ nói:
- Bây giờ chỉ còn lại cái xác bướm không hồn!
(Trích Bóng người trên sương mù, Nhất Linh, in trong Anh phải sống, NXB Đời nay, 1934)
Trả lời cho các câu 51, 52, 53, 54, 55, 56, 57, 58, 59, 60 dưới đây:
Ngữ cảnh và tâm trạng mà tác giả muốn truyền đạt qua bóng người trên sương mù?
Đáp án đúng là: B
Đọc hiểu nội dung toàn bài, suy ra nội dung chính.
Đáp án cần chọn là: B
Truyện được kể theo ngôi thứ nhất hay thứ ba?
Ngôi kể .
Đáp án đúng là: thứ nhất
Liên hệ với kiến thức về ngôi kể, đối chiếu với đặc điểm của bài đọc.
Đáp án cần điền là: thứ nhất
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Tình huống nhân vật tránh được tai nạn nhưng không tránh được cái chết bi thương của người vợ đã mở ra một hành trình tìm kiếm ý nghĩa và giác ngộ về cuộc sống.
Đúng hay sai?
Đáp án đúng là: A
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Đáp án cần chọn là: A
Từ thông tin của bài đọc, hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí.
"Bóng người trên sương mù" của Nhất Linh là một bức tranh về cuộc sống, nơi tác giả khéo léo làm nổi bật những đầy ý nghĩa. Cái chết của người vợ không chỉ là sự kiện đau lòng, mà còn là để nhân vật nhìn nhận lại giá trị của cuộc sống.
Đáp án đúng là: đa chiều; khía cạnh; cơ hội
Dựa vào logic câu từ và hiểu biết có được qua bài đọc.
Đáp án cần chọn là: đa chiều; khía cạnh; cơ hội
Nội dung của đoạn [5] là:
(chọn nhiều đáp án)
Đáp án đúng là: B; D
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Đáp án cần chọn là: B; D
Điền một từ không quá hai tiếng có trong bài đọc vào chỗ trống.
Đoạn trích mô tả những quan tâm, tò mò và phân vân của nhân vật trước “bóng người”, làm nổi bật sự lo lắng của anh trước cảnh mênh mông.
Đáp án đúng là: sương mù
Đọc hiểu nội dung toàn bài, kết hợp với ngữ cảnh câu văn.
Đáp án cần điền là: sương mù
“Bóng người trên sương mù” có ý nghĩa gì trong ngữ cảnh của đoạn trích?
Đáp án đúng là: C
Đọc hiểu nội dung toàn bài, nắm được ý nghĩa hình tượng mà tác giả muốn gửi gắm.
Đáp án cần chọn là: C
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Ông Chánh trong truyện là một nhân vật gặp đầy khó khăn và thách thức trong cuộc sống.
Đúng hay sai?
Đáp án đúng là: B
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Đáp án cần chọn là: B
Từ thông tin của bài đọc, hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí.
1/ Tâm trạng của nhân vật khi vừa thoát khỏi tai nạn tàu hỏa:
2/ Tâm trạng của nhân vật khi hay tin cái chết của vợ:
3/ Tâm trạng của nhân vật khi gặp lại người bạn cũ:
Đáp án đúng là: kinh ngạc; hối tiếc; vui mừng
Dựa vào logic câu từ và hiểu biết có được qua bài đọc.
Đáp án cần chọn là: kinh ngạc; hối tiếc; vui mừng
Ý nghĩa hình tượng “con bướm” trong đoạn trích trên:
(chọn nhiều đáp án)
Đáp án đúng là: A; C
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Đáp án cần chọn là: A; C
Phần 3: Tư duy khoa học/Giải quyết vấn đề
Bong bóng bay được dùng nhiều trong dịp lễ hội, vui chơi giải trí. Để tạo ra bóng bay, một loại khí nhẹ được bơm vào các quả bóng. Hiện nay người ta thường sử dụng một trong hai loại khí: khí hydrogen hoặc helium. Hydrogen là loại khí nhẹ nhất; khi ở trong không khí và gặp một tia lửa hoặc nguồn nhiệt, hydrogen dễ dàng tác dụng với oxygen tạo ra phản ứng cháy, nổ và sinh ra một nhiệt lượng lớn. Helium là một loại khí trơ, thường không có phản ứng hóa học với các chất khác.
Cho rằng khi bơm vào bóng, khối lượng riêng của khí hydrogen là \({\rho _1} = 0,1\,\,g/l\), của khí helium là \({\rho _2} = 0,2\,\,g/l\).
Trả lời cho các câu 61, 62, 63, 64, 65, 66 dưới đây:
Điền từ thích hợp vào chỗ trống:
Để làm bóng bay có thể bay lên, người ta thường bơm vào bóng bay các loại khí có khối lượng riêng nhỏ hơn khối lượng riêng của .
Đáp án đúng là: không khí
Dựa vào thông tin bài cung cấp
Đáp án cần điền là: không khí
Kéo thả đáp án thích hợp vào chỗ trống:
Hydrogen hơn helium, nên bóng bơm có thể bay nhanh hơn một chút so với bóng bơm .
Đáp án đúng là: nhẹ; hydrogen; helium
Dựa vào thông tin bài cung cấp
Vận dụng lí thuyết về lực nâng
Đáp án cần chọn là: nhẹ; hydrogen; helium
Một khí cầu thám không hình cầu được bơm đầy khí helium đến thể tích \(34\,\,{m^3}\). Khi bơm xong, helium trong khí cầu có nhiệt độ \({27^0}C\), áp suất \(1,{2.10^5}\,\,Pa\). Khí cầu bay lên cao, càng lên cao áp suất khí quyển càng giảm, thể tích khí cầu tăng lên. Biết vỏ khí cầu không bị vỡ khi thể tích khí không vượt quá 27 lần thể tích ban đầu. Khối lượng khí helium cần bơm vào khí cầu gần nhất với
Đáp án đúng là: D
Sử dụng phương trình Clapeyron: pV = nRT
Đáp án cần chọn là: D
Với khí cầu trên, nếu bơm khí trong thời gian 2 phút kể từ khi trong vỏ khí cầu không có khí đến khi đầy, cần dùng máy bơm có thể bơm được trung bình bao nhiêu gam khí mỗi giây?
Đáp án đúng là: B
Phân tích câu hỏi và thông tin bài cung cấp
Đáp án cần chọn là: B
Cứ lên cao 10 m thì thấy áp suất khí quyển giảm đi 1 mmHg, khi đó độ cao lớn nhất khí cầu đạt được là:
Đáp án đúng là: C
Sử dụng phương trình trạng thái khí lí tưởng
Đáp án cần chọn là: C
Hãy chọn các đáp án đúng trong các nhận xét sau:
Đáp án đúng là: A; C
Dựa vào thông tin bài cung cấp
Đáp án cần chọn là: A; C
Nhà máy điện mặt trời làm từ nhiều tấm gương khổng lồ. Những tấm gương lớn tập trung ánh sáng mặt trời để nung chảy muối nitrate, từ đó sản xuất lượng điện năng đủ phục vụ cho cả một thành phố.
Theo Business Insider, nhà máy điện Crescent Dune có nhiều tấm gương phản xạ ánh sáng, mỗi tấm như vậy có diện tích 115 mét vuông, được đặt xung quanh một tháp trung tâm. Tổng cộng có tất cả 10000 tấm, được lắp đặt từ cuối năm 2015, trên khu vực rộng 1,2 triệu mét vuông, thuộc Crescent Dune. Đó là một nhà máy điện năng lượng mặt trời tập trung (Concentrating Solar Power - CSP) ở sa mạc Nevada, Mỹ.
Theo Kevin Smith, một trong những nhà sáng lập dự án, loại tấm này không phải là các tấm quang điện (Photovoltaic - PV) truyền thống thường được đặt trên mái nhà hay các nơi khai thác năng lượng mặt trời khắp thế giới.
“Nhược điểm của quang điện là tính không liên tục”, Smith nói. “Khi Mặt Trời lặn là không thể sử dụng được tiếp”.
Chúng là những tấm gương thực sự, hướng theo đường đi của Mặt Trời trong ngày như hoa hướng dương. Chúng sẽ tập trung phản xạ ánh sáng Mặt Trời chính xác vào đỉnh tháp. Tại đây, năng lượng sẽ được tích trữ vào muối nóng chảy.
Theo Kevin Smith, đây là “công nghệ lưu trữ năng lượng tiên tiến nhất”, hơn hẳn lưu trữ vào nước, vào pin hay vào các chảo parabol chứa đầy dầu. Tháp trung tâm là nơi chứa khoảng 25000 tấn muối nitrate của sodium và potassium (có kèm theo phụ gia) có nhiệt độ \({288^0}C\). Ở nhiệt độ này, muối tồn tại dưới dạng lỏng.
“Chúng tôi sẽ nung nóng muối tới nhiệt độ \({560^0}C\). Muối sau đó sẽ chảy xuống dưới tháp và được giữ ở trong một bể chứa lớn”, Smith cho biết.
Muối nóng chảy giữ nhiệt độ rất tốt, và nhiệt sẽ được chuyển thành điện qua các turbine hơi nước truyền thống. Crescent Dune có công suất 110 MW, hệ thống nảy có thể điện cho nhu cầu của 75000 hộ gia đinh tại Nevada, thời lượng 24 giờ mỗi ngày. Smith cho rằng CSP không chỉ là sự thay thế cho các tấm quang điện truyền thống mà còn là đối thủ cạnh tranh tiềm năng với nhiên liệu thông thường. Nó sẽ thay thế cho nhiên liệu hóa thạch, thậm chí là nhiên liệu hạt nhân. Công ty Solar Reverse của Smith đã phát triển các nhà máy điện CSP rẻ hơn, năng lượng cao hơn và có kế hoạch xây dựng các nhà máy điện tương tự Crescent Dune tại Nam Phi, Chile và Trung Quốc.
Trả lời cho các câu 67, 68, 69, 70, 71, 72 dưới đây:
Tổng diện tích gương của nhà máy điện Crescent Dune là
Đáp án đúng là: B
Dựa vào thông tin từ bài cung cấp
Đáp án cần chọn là: B
Điền số thích hợp vào chỗ trống:
Mỗi gia đình ở Nevada tiêu thụ trong 30 ngày hết trung bình cỡ số điện?
Đáp án đúng là: 1056
Sử dụng công thức tính điện năng: A = P.t
Dựa vào lí thuyết về hiện suất: \(H = \dfrac{{{A_i}}}{A}\)
Đáp án cần điền là: 1056
Nếu mỗi mét vuông kính nhận được ánh sáng mặt trời có công suất trung bình 600 W thì hiệu suất nhà máy điện Crescent Dune là
Đáp án đúng là: C
Xác định công suất cung cấp cho kính dựa trên dữ liệu đề bài
Dựa vào công thức tính hiệu suất
Đáp án cần chọn là: C
Nhà máy điện CSP Ivanpah ở California, được xây dựng trước, không dùng muối nóng chảy mà dùng dầu được đun tới nhiệt độ tối đa là \({400^0}C\). Để vận hành nhà máy điện hơi nước, cần đun nước bay hơi ở áp suất cao tới \({288^0}C\). Cho khối lượng riêng của dầu \({d_1} = 800\,\,kg.{m^{ - 3}}\) và muối lỏng là \({d_2} = 2200\,\,kg.{m^{ - 3}}\); nhiệt dung riêng của dầu \({c_1} = 2400\,\,J.k{g^{ - 1}}.{K^{ - 1}}\) và muối lỏng là \({c_2} = 1100\,\,J.k{g^{ - 1}}.{K^{ - 1}}\). Theo em , khi có cùng một thể tích bình chứa, nhiệt lượng để vận hành nhà máy điện của muối nóng chảy tích trữ được nhiều hơn so với dầu bao nhiêu lần?
Đáp án đúng là: D
Phân tích đề bài
Sử dụng công thức tính nhiệt lượng: \(Q = mc\Delta t\)
Đáp án cần chọn là: D
Kéo thả các đáp án thích hợp vào chỗ trống:
Ngoài những nhược điểm như chi phí lắp đặt ban đầu khá cao, cần cường độ ánh sáng mặt trời mạnh, hoạt động ít hiệu quả khi trời mưa và thời tiết lạnh thì những ưu điểm nổi trội của CSP phải kể đến như sau:
Nhiệt điện Mặt Trời là nguồn năng lượng vô tận, dễ cài đặt, có thể cài đặt cho người dùng là cá nhân, tổ chức hoặc quy mô lớn hơn, không phát ra tiếng ồn. Chi phí bảo trì, bảo dưỡng thấp. Một trong những lợi thế quan trọng nhất về môi trường của năng lượng Mặt Trời là nó không có carbon dioxide hoặc các khí khác trong sản xuất điện, nên nó là nguồn năng lượng sạch. Năng lượng Mặt Trời sẽ thay thế cho . Bạn không thể cấp điện cho cả một thành phố chỉ với quang điện và phong điện, nhưng có thể với CSP nhờ năng lượng lưu trữ của nó. CSP sử dụng ít hơn các nhà máy nhiệt điện hay điện hạt nhân và chỉ chiếm một diện tích nhỏ hơn rất nhiều so với nhà máy nhiệt điện đốt than.
Đáp án đúng là: sạch; phát thải; nhiên liệu hóa thạch; nước
Dựa vào thông tin bài cung cấp
Đáp án cần chọn là: sạch; phát thải; nhiên liệu hóa thạch; nước
Phát biểu sau đây đúng hay sai:
“Theo Kevin Smith, công nghệ CSP có tiềm năng lớn có thể thay thế cho nhiên liệu hóa thạch và nhiên liệu hạt nhân trong tương lai.”
Đáp án đúng là: A
Dựa vào thông tin bài cung cấp
Đáp án cần chọn là: A
Khi hòa tan các chất có liên kết ion hoặc liên kết cộng hóa trị có cực vào trong dung môi phân cực (ví dụ như nước, rượu,…) thì do sự tương tác với các phân tử lưỡng cực của dung môi mà các phân tử chất tan sẽ phân li hoàn toàn hoặc một phần thành các ion mang điện tích trái dấu, tồn tại dưới dạng ion solvat hóa (đối với dung môi ion nước là ion hydrate hóa). Như vậy các chất có khả năng phân li thành các ion được gọi là chất điện li, và quá trình phân li thành ion được gọi là quá trình điện li.
Ví dụ khi hòa tan chất điện li \(MX\) vào nước:
![]()
Thông thường ta không biết chính xác số phân tử nước \(x,y\) trong ion hydrate hóa nên người ta biểu diễn sự phân li theo sơ đồ đơn giản: MX ⇌ Mn+ + Xn- (1) , với ngầm hiểu là \({M^{n + }},{X^{n - }}\) chỉ là các ion hydrate hóa.
Mức độ phân li thành ion của các chất điện li phụ thuộc vào bản chất của các chất điện li và bản chất của dung môi. Ví dụ: \(HCl\) trong nước là chất điện li mạnh, còn \(C{H_3}COOH\) lại là chất điện li yếu. Để đặc trưng định lượng sự phân li của các chất điện li, người ta dựa vào độ điện li α và hằng số điện li \(K\).
Độ điện li α là tỉ số mol \(n\) của chất đã phân li thành ion với tổng số mol \({n_0}\) của chất tan trong dung dịch:
\(\alpha = \dfrac{n}{{{n_0}}}(*)\)
Nếu chia cả hai số hạng của biểu thức (*) cho thể tích \(V\) của dung dịch thì:
\(\alpha = \) Nồng độ chất đã điện li / Tổng nồng độ chất đã điện li
\(\alpha \) sẽ có các giá trị dao động từ 0 đến 1: \(0 \le \alpha \le 1\)
\(\alpha = 0\) đối với chất không điện li;
\(\alpha = 1\) đối với chất điện li hoàn toàn.
Áp dụng định luật tác dụng khối lượng cho cân bằng (1), ta có: \({K^C} = \dfrac{{[{M^{n + }}][{X^{n - }}]}}{{[MX]}}\)
Ở đât \([i]\) chỉ nồng độ của cấu tử \(i\) trong dung dịch ở trạng thái cân bằng.
\({K^C}\) là hằng số điện li nồng độ, phụ thuộc vào bản chất của chất li, vào dung môi, vào nhiệt độ, Trong dung dịch loãng, \({K^C}\) không phụ thuộc vào nồng độ chất điện li.
Trả lời cho các câu 73, 74, 75, 76, 77, 78, 79 dưới đây:
Nhận định nào dưới đây là không chính xác?
Đáp án đúng là: C
Dựa vào đoạn thông tin mô tả về quá trình điện li, chất điện li và kiến thức thực tế.
Đáp án cần chọn là: C
Biểu thức nào dưới đây là đặc trưng định lượng cho sự phân li của ion \({M^{n + }}\) trong nước ở trạng thái cân bằng?
Đáp án đúng là: A
- Dựa vào 2 đoạn thông tin:
Đoạn 1: Độ điện li α là tỉ số mol \(n\) của chất đã phân li thành ion với tổng số mol \({n_0}\) của chất tan trong dung dịch:
\(\alpha = \dfrac{n}{{{n_0}}}(*)\)
Nếu chia cả hai số hạng của biểu thức (*) cho thể tích \(V\) của dung dịch thì:
\(\alpha = \) Nồng độ chất đã điện li / Tổng nồng độ chất đã điện li
Đoạn 2: Áp dụng định luật tác dụng khối lượng cho cân bằng (1), ta có: \({K^C} = \dfrac{{[{M^{n + }}][{X^{n - }}]}}{{[MX]}}\)
Ở đât \([i]\) chỉ nồng độ của cấu tử \(i\) trong dung dịch ở trạng thái cân bằng.
Đáp án cần chọn là: A
Điền từ không quá 1 tiếng để hoàn thành nhận định sau?
Nồng độ chất đã phân li bằng ______ nồng độ chất điện li với độ điện li.
Đáp án đúng là: tích
Dựa vào biểu thức về độ điện li α.
Đáp án cần điền là: tích
Kéo thả cụm từ thích hợp vào chỗ trống?
Trong trường hợp chất \(MX\) phân li cực ít trong nước (\(\alpha < < 1\)), biểu thức liên hệ giữa hằng số phân li, độ điện li và nồng độ của chất điện li ban đầu là: \(\alpha = \sqrt {\dfrac{{{K^C}}}{C}} \). Hoàn thành các nhận định dưới đây
- Độ điện li với hằng số phân li \(K\). Nếu hằng số phân li càng thì chất điện li càng mạnh, phân li càng nhiều.
- Độ điện li với nồng độ. Đối với một chất nhất định (\(K\) không đổi) thì trong dung dịch càng loãng, chất điện li càng nhiều.
Đáp án đúng là: tỉ lệ thuận; lớn ; tỉ lệ nghịch
Theo biểu thức liên hệ giữa hằng số phân li, độ điện li và nồng độ của chất điện li ban đầu là: \(\alpha = \sqrt {\dfrac{{{K^C}}}{C}} \), độ điện li tỉ lệ thuận với hằng số phân li và tỉ lệ nghịch với nồng độ của chất điện li.
Đáp án cần chọn là: tỉ lệ thuận; lớn ; tỉ lệ nghịch
Dựa vào dữ liệu trong các câu trên để giải quyết bài tập sau
Trong dung dịch \(C{H_3}COOH\,\,1,00M\), tỉ lệ acid ion hóa là 0,417%. Thông qua tính toán thấy hằng số phân li của acetic acid trong điều kiện này \(a{.10^{ - 4}}\). Giá trị của \(a\) là ________. (Làm tròn kết quả đến số thập phân thứ hai).
Đáp án đúng là: 17,39
Theo đầu bài tỉ lệ acid ion hóa là 0,417% ⇒ \({\alpha _{C{H_3}COOH}} = 0,00417 < < 1\) nên có thể tính toán hằng số phân li của acetic acid theo biểu thức \(\alpha = \sqrt {\dfrac{{{K^C}}}{C}} \).
Đáp án cần điền là: 17,39
Trong dung dịch acetic acid, có thể có
Đáp án đúng là: A; B; C; D
Acetic acid là một acid yếu nên trong dung dịch phân li theo mũi tên hai chiều.
Đáp án cần chọn là: A; B; C; D
Tính pH của hệ là hỗn hợp của HCl 0,01M và H2S 0,1M, biết Ka1 (H2S) = 10-7,02 (Ka1 là hằng số phân li acid nấc thứ nhất) và bỏ qua nấc phân li thứ hai của acid H2S. (Điền kết quả đến số thập phân thứ hai).
Đáp án đúng là: 1,99
Công thức tính pH là \(pH = - \lg [{H^ + }]\).
Đáp án cần điền là: 1,99
Trong tự nhiên, các quá trình tự diễn biến xảy ra theo xu hướng: làm giảm năng lượng hóa học - enthalpy (\(\Delta H < 0\)) và làm tăng độ mất trật tự của hệ - entropy (\(\Delta S > 0\)). Khi xét đến quá trình hóa học có tự xảy ra hay không phải xét đồng thời cả biến thiên enthalpy và biến thiên entropy, thông qua biến thiên năng lượng Gibbs (\(\Delta G\)) (ở nhiệt độ và áp suất không đổi): \({\Delta _r}G_T^o = {\Delta _r}H_T^o - T.{\Delta _r}S_T^o\).
Trong đó:
\({\Delta _r}H_T^o\,(kJ/mol)\) là biến thiên enthalpy chuẩn của phản ứng ở nhiệt độ T, bằng tổng nhiệt tạo thành chuẩn của các chất sản phẩm trừ đi tổng nhiệt tạo thành của các chất tham gia. Phản ứng tỏa nhiệt thì \({\Delta _r}H^\circ \) có giá trị âm còn phản ứng thu nhiệt thì \({\Delta _r}H^\circ \) có giá trị dương.
\({\Delta _r}S_T^o\,(J/mol.K)\) là biến thiên entropy chuẩn của phản ứng ở nhiệt độ T, bằng tổng entropy chuẩn của các chất sản phẩm trừ đi tổng entropy của các chất tham gia;
\(T\) là nhiệt độ tại đó xảy ra phản ứng (theo thang Kelvin);
\({\Delta _r}G_T^o\) là biến thiên năng lượng tự do Gibbs chuẩn của phản ứng ở nhiệt độ \(T\).
Dựa vào \({\Delta _r}G_T^o\) có thể dự đoán hoặc giải thích được chiều hướng của một phản ứng hóa học ở nhiệt độ \(T\):
\({\Delta _r}G_T^o < 0\) phản ứng sẽ tự xảy ra, giá trị \({\Delta _r}G_T^o\) càng âm, phản ứng càng dễ xảy ra;
\({\Delta _r}G_T^o = 0\) phản ứng đạt trạng thái cân bằng;
\({\Delta _r}G_T^o > 0\) phản ứng không tự xảy ra.
Trả lời cho các câu 80, 81, 82, 83, 84, 85 dưới đây:
Kéo thả cụm từ thích hợp vào chỗ trống
Để một phản ứng không tự xảy ra ở mọi nhiệt độ thì biến thiên enthalpy của phản ứng đó0 và biến thiên entropy của phản ứng đó0.
Đáp án đúng là: lớn hơn; nhỏ hơn
Biến đổi biểu thức \({\Delta _r}G_T^o = {\Delta _r}H_T^o - T.{\Delta _r}S_T^o\) để rút ra giá trị của biến thiên enthalpy và biến thiên entropy của phản ứng so với 0.
Đáp án cần chọn là: lớn hơn; nhỏ hơn
Các nhận định sau là đúng hay sai?
| Đúng | Sai | |
|---|---|---|
| a) Phản ứng tỏa nhiệt luôn có khả năng tự xảy ra.\(\) | ||
| b) Có thể kết luận ngay là phản ứng không tự xảy ra khi \({\Delta _r}G_T^o\) của phản ứng dương tại điều kiện đang xét. | ||
| c) Có thể căn cứ vào hiệu ứng nhiệt để dự đoán khả năng tự phát của phản ứng ở nhiệt độ thường. | ||
| d) Ở ≈ 1000K, khả năng tự phát của phản ứng hóa học chủ yếu chỉ phụ thuộc vào giá trị biến thiên enthalpy. |
Đáp án đúng là: S; Đ; S; S
Biến đổi biểu thức \({\Delta _r}G_T^o = {\Delta _r}H_T^o - T.{\Delta _r}S_T^o\) để rút ra giá trị của biến thiên enthalpy và biến thiên entropy của phản ứng tại các điều kiện ứng với từng nhận định.
Đáp án cần chọn là: S; Đ; S; S
Nhận định nào dưới đây là chính xác?
Phản ứng thu nhiệt mạnh
Đáp án đúng là: D
- Phản ứng thu nhiệt mạnh: \({\Delta _r}H_T^o > 0\) (biến thiên enthalpy dương).
- Điều kiện tự phát: \({\Delta _r}G_T^o < 0\) (biến thiên năng lượng tự do Gibbs âm).
- Công thức Gibbs: \({\Delta _r}G_T^o = {\Delta _r}H_T^o - T.{\Delta _r}S_T^o\). Phản ứng thu nhiệt mạnh là phản ứng có biến thiên enthalpy nhỏ hơn 0 và rất âm.
Đáp án cần chọn là: D
Chọn các đáp án đúng
Một phản ứng có thể tự xảy ra khi
Đáp án đúng là: A; C; D
- Điều kiện tự phát: \({\Delta _r}G_T^o < 0\) (biến thiên năng lượng tự do Gibbs âm).
- Công thức Gibbs: \({\Delta _r}G_T^o = {\Delta _r}H_T^o - T.{\Delta _r}S_T^o\). Phản ứng thu nhiệt mạnh là phản ứng có biến thiên enthalpy nhỏ hơn 0 và rất âm.
Đáp án cần chọn là: A; C; D
Điền từ không quá một tiếng và số nguyên thích hợp vào chỗ trống
Biến thiên enthalpy và entropy của phản ứng \(2S{O_2}\left( g \right) + {O_2}\left( g \right) \to 2S{O_3}\left( g \right)\)ở 25oC lần lượt là \({\Delta _r}{H^o} = - 198{\rm{ }}kJ\)và \({\Delta _r}{S^o} = - 187{\rm{ }}J/K\).
- Khi tăng nhiệt độ, giá trị của \({\Delta _r}{G^o}\) .
- Tại khoảng nhiệt độ lớn hơn K thì phản ứng tự xảy ra.
Đáp án đúng là: tăng; 1059
Công thức Gibbs: \({\Delta _r}G_T^o = {\Delta _r}H_T^o - T.{\Delta _r}S_T^o\). Phản ứng thu nhiệt mạnh là phản ứng có biến thiên enthalpy nhỏ hơn 0 và rất âm.
Đáp án cần điền là: tăng; 1059
Xét phản ứng sau: \(CaC{O_3}\left( s \right) \to CaO\left( s \right) + C{O_2}\left( g \right)\). Giả sử giá trị enthalpy và entropy của phản ứng không thay đổi theo nhiệt độ. Mối liên hệ giữa \({\Delta _r}G^\circ \)và T (K) của phản ứng trên như sau:
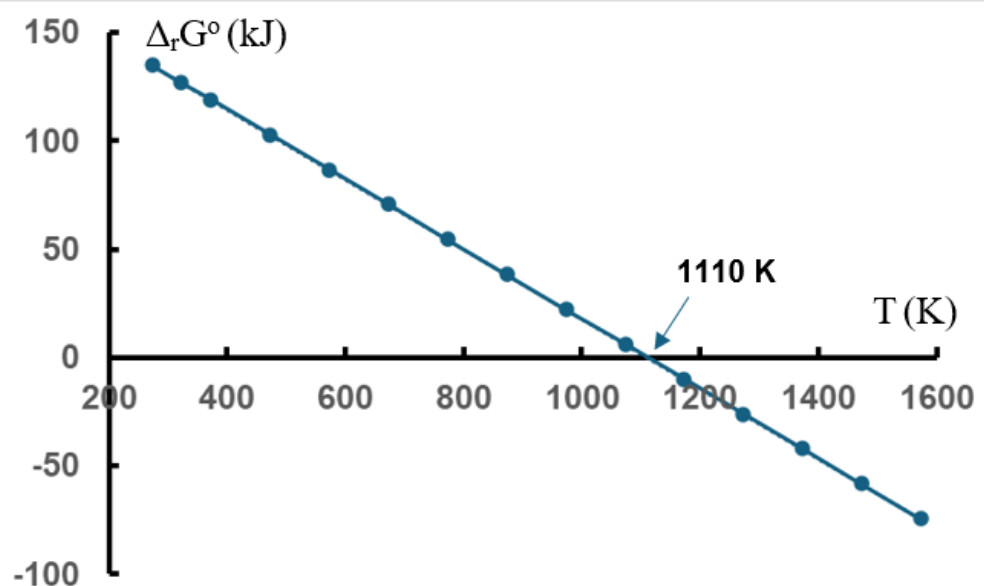
Hãy chọn nhận xét sai
Đáp án đúng là: D
Dựa vào biểu đồ và mối quan hệ giữa các đại lượng trong biểu thức tính biến thiên năng lượng Gibbs.
Đáp án cần chọn là: D
Đọc đoạn thông tin sau và trả lời câu hỏi:
HỆ NHÓM MÁU ABO VÀ Rh Ở NGƯỜI
Hệ nhóm máu ABO lần đầu tiên được xác định bởi nhà miễn dịch học người Áo Karl Landsteiner vào năm 1901. Trong đó, các nhóm máu được phân loại dựa trên các đặc tính di truyền của các tế bào hồng cầu (hồng cầu), cụ thể được xác định bởi sự hiện diện hay vắng mặt của các kháng nguyên A và B trên bề mặt của các tế bào hồng cầu. Do đó, có thể chia thành bốn nhóm máu: nhóm A, nhóm B, nhóm O hoặc nhóm AB như thể hiện trong bảng 1.
Bảng 1. Đặc điểm các nhóm máu thuộc hệ nhóm máu ABO và Rh.
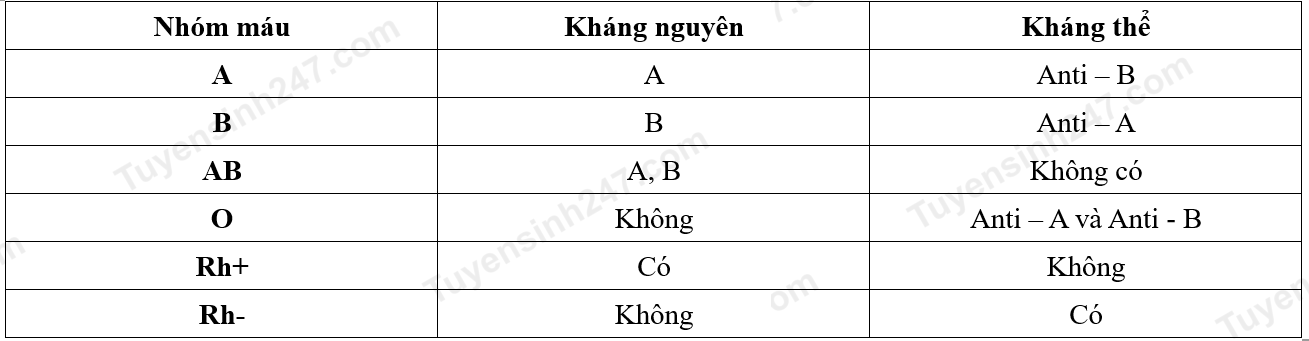
Trong huyết tương của người nhóm A có kháng thể anti-B, huyết tương của người nhóm máu B có kháng thể anti-A, huyết tương của người nhóm O có cả kháng thể anti-A v à anti-B, huyết tương của người nhóm AB không có cả 2 kháng thể này. Khi máu không tương xứng được truyền cho nhau, kháng thể anti-A hoặc anti-B trong huyết tương sẽ trộn với kháng nguyên A hoặc B trên màng hồng cầu, chúng sẽ kết dính với nhau.
Máu cũng có thể được phân loại là Rh dương tính (Rh+) hoặc Rh âm tính (Rh-), dựa trên sự hiện diện hay vắng mặt của một kháng nguyên khác trên các tế bào hồng cầu: người có kháng nguyên D trên màng hồng cầu được gọi là Rh dương tính (Rh+), người không có kháng nguyên D trên màng hồng cầu được gọi là Rh âm tính (Rh-). Khi truyền máu Rh+ cho người Rh- thì những người Rh- sẽ sản xuất kháng thể anti-Rh. Nếu lần sau người Rh- lại nhận máu Rh+ thì kháng thể anti-Rh trong cơ thể người nhận sẽ làm ngưng kết hồng cầu cho Rh+ và sẽ xảy ra phản ứng truyền máu.
Tỷ lệ các nhóm máu ở người được thể hiện trong hình dưới đây:
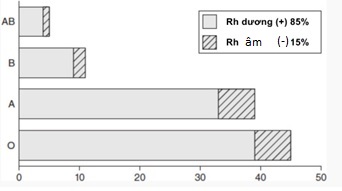
Hình 1. Sự phân bố nhóm máu ở người.
Trả lời cho các câu 86, 87, 88, 89, 90, 91, 92 dưới đây:
Điền đáp án chính xác vào chỗ trống
Để xác định được nhóm máu ở người, người ta dựa vào sự hiện diện hay vắng mặt của các trên bề mặt của các tế bào hồng cầu. Trong huyết tương có các loại chống lại các kháng nguyên. Sự phân loại này có thể chia thành nhóm máu.
Đáp án đúng là: kháng nguyên; kháng thể; bốn
Đọc thông tin trên bài đọc để tìm từ khóa chính xác
Đáp án cần chọn là: kháng nguyên; kháng thể; bốn
Theo em, tên của từng nhóm máu ABO được lấy từ:
Đáp án đúng là: B
Đọc thông tin bài đọc và phân tích bảng 1.
Đáp án cần chọn là: B
Khi nói về đặc điểm của các nhóm máu, những phát biểu nào sau đây là Đúng?
Đáp án đúng là: A; C; D
Phân tích thông tin trong bảng 1 để xác định từng nhóm máu có loại kháng nguyên và kháng thể nào tương ứng.
Đáp án cần chọn là: A; C; D
Kéo thả đáp án chính xác vào chỗ trống
Nhóm máu có kháng nguyên trên bề mặt hồng cầu và không có kháng thể kháng Rh trong huyết thanh.
Nhóm máu không có kháng nguyên trên bề mặt hồng cầu và có kháng thể kháng Rh trong huyết thanh.
Đáp án đúng là: Rh+; Rh-
Đọc thông tin trên bài đọc để tìm từ khóa chính xác về hai loại nhóm máu Rh
Đáp án cần chọn là: Rh+; Rh-
Dựa vào đặc điểm các nhóm máu thuộc hệ nhóm máu ABO và Rh, hãy cho biết máu chứa kháng thể kháng A, kháng Rh và kháng nguyên B là?
Đáp án đúng là: D
Dựa vào bảng phân loại 4 nhóm máu của hệ ABO và đoạn thông tin về nhóm máu Rh
Đáp án cần chọn là: D
Nhóm máu A không được truyền vào những người có nhóm máu nào?
Đáp án đúng là: B; D
Dựa vào bảng phân loại 4 nhóm máu của hệ ABO, không thể truyền máu khi xuất hiện hiện tượng ngưng kết giữa kháng nguyên và kháng thể cùng loại. Ví dụ: kháng nguyên A và kháng thể kháng A (anti A)
Đáp án cần chọn là: B; D
Những nhận định dưới đây là đúng hay sai?
| Đúng | Sai | |
|---|---|---|
| a) Nhóm máu O là nhóm máu chuyên cho. | ||
| b) Nhóm máu chiếm tỉ lệ cao nhất là nhóm máu O | ||
| c) Nhóm máu hiếm nhất là máu AB+ | ||
| d) Khi truyền máu Rh+ cho người Rh- thì những người Rh- thì ngay lần đầu tiên sẽ gây phản ứng ngưng kết |
Đáp án đúng là: Đ; S; S; S
Dựa vào thông tin bài đọc, đặc điểm của từng loại nhóm máu trong bảng 1 và tỷ lệ các loại nhóm máu trong hình 1 để phân tích từng câu
Đáp án cần chọn là: Đ; S; S; S
Đọc đoạn thông tin sau và trả lời câu hỏi:
THUỐC KHÁNG SINH DIỆT VI KHUẨN
Mặc dù nhiều dạng vi khuẩn rất hữu ích cho sức khỏe con người, nhưng chúng cũng có thể gây bệnh và thậm chí tử vong do nhiễm trùng nặng. Thuốc kháng sinh là một nhóm thuốc được sử dụng để chống nhiễm trùng do vi khuẩn, nó ức chế hoạt động sống của vi khuẩn và giết chết tế bào vi khuẩn.
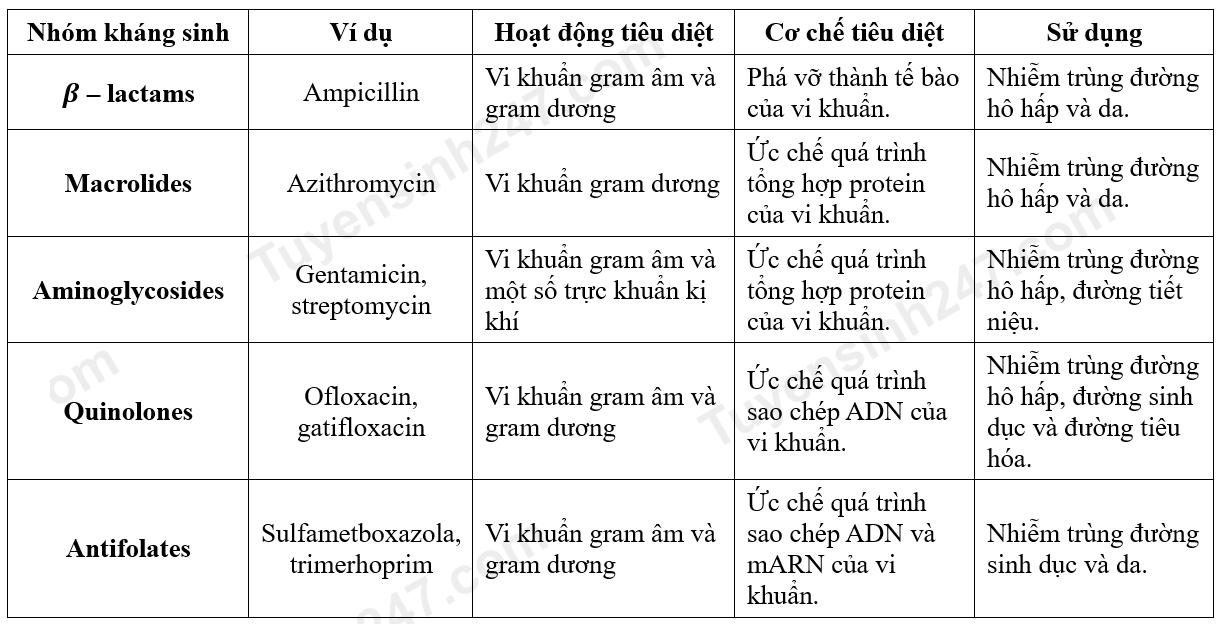
Bảng 1. Đặc điểm, cơ chế hoạt động và chỉ định sử dụng của một số nhóm kháng sinh.
Hiệu quả của một số loại kháng sinh chống lại một loại vi khuẩn được biết là gây nhiễm trùng da thông thường đã được thử nghiệm. Thuốc được đưa vào nuôi cấy vi khuẩn hoặc kết hợp với sulfamethoxazole (tạo thành các hợp chất SMX) và được đưa vào nuôi cấy vi khuẩn.
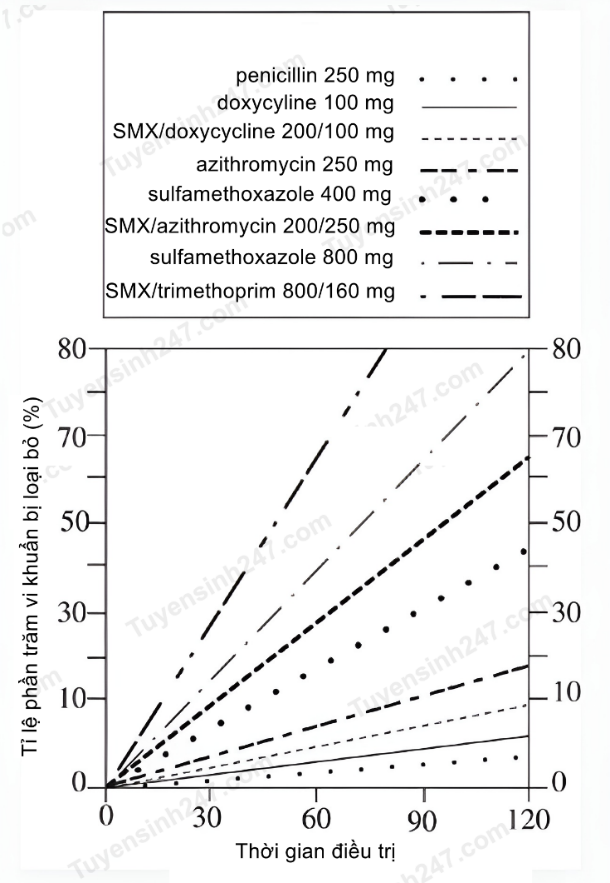
Hình 1. Một số nhóm kháng sinh và khả năng diệt khuẩn của chúng.
Sử dụng thông tin bài đọc để trả lời các câu hỏi sau:
Trả lời cho các câu 93, 94, 95, 96, 97, 98, 99, 100 dưới đây:
Thuốc kháng sinh dưới đây thuộc nhóm kháng sinh nào?
Đáp án đúng là: A
Xác định vị trí của Ampicillin trong bảng tổng hợp các loại thuốc kháng sinh để xác định nhóm kháng sinh tương ứng
Đáp án cần chọn là: A
Để diệt những bệnh nhiễm trùng gây nên bởi vi khuẩn gram dương thì người ta cần dùng những loại thuốc kháng sinh nào dưới đây?
Đáp án đúng là: A; B; D; E
Xác định vị trí có từ khóa “vi khuẩn gram dương” trong bảng tổng hợp các loại thuốc kháng sinh để xác định nhóm kháng sinh tương ứng
Đáp án cần chọn là: A; B; D; E
Đâu là cơ chế hoạt động diệt khuẩn của nhóm kháng sinh Antifolates?
Đáp án đúng là: A
Xác định vị trí có từ khóa “kháng sinh Antifolates” trong bảng tổng hợp các loại thuốc kháng sinh để xác định cơ chế tương ứng
Đáp án cần chọn là: A
Theo em, với một bệnh nhân bị bệnh nhiễm trùng da do vi khuẩn gây ra thì nên dùng loại thuốc kháng sinh nào để đạt được hiệu quả điều trị tốt nhất?
Đáp án đúng là: D
So sánh các đường thể hiện hiệu quả diệt khuẩn của các loại thuốc kháng sinh trong biểu đồ để suy ra
Đáp án cần chọn là: D
Điền đáp án chính xác vào chỗ trống
Khi sử dụng cùng một loại thuốc kháng sinh nhưng khi sử dụng với liều lượng _______ hơn thì hiệu quả điều trị sẽ cao hơn.
Đáp án đúng là: cao/lớn
So sánh các đường thể hiện hiệu quả diệt khuẩn của từng cặp loại thuốc kháng sinh với các liều lượng khác nhau trong biểu đồ để suy ra
Đáp án cần điền là: cao/lớn
Kéo thả đáp án chính xác vào chỗ trống.
Khi kết hợp thuốc kháng sinh với hợp chất SMX thì hiệu quả điều trị bệnh
Đáp án đúng là: giảm đi
So sánh các đường thể hiện hiệu quả diệt khuẩn của từng cặp loại thuốc kháng sinh với các hai cách thức khác nhau: chỉ kháng sinh và khi kết hợp với hợp chất SMX trong biểu đồ để suy ra
Đáp án cần chọn là: giảm đi
Điền đáp án thích hợp vào chỗ trống
Thuốc kháng sinh là nhóm thuốc được sử dụng để chống nhiễm trùng do _________
Đáp án đúng là: vi khuẩn
Đọc kĩ thông tin đoạn đọc để tìm từ khóa.
Đáp án cần điền là: vi khuẩn
Những nhận định sau đây Đúng hay Sai?
| Đúng | Sai | |
|---|---|---|
| a) Nhóm kháng sinh β-lactam ức chế sự hình thành tế bào vi khuẩn mới | ||
| b) Tất cả các loại thuốc kháng sinh khi kết hợp với sulfamethoxazole (tạo thành các hợp chất SMX) đều cho hiệu quả diệt khuẩn tốt hơn | ||
| c) Thời gian sử dụng thuốc tăng gấp đôi thì hiệu quả diệt khuẩn tăng gấp đôi |
Đáp án đúng là: S; Đ; S
a) Xác định vị trí có từ khóa “kháng sinh β-lactam” trong bảng tổng hợp các loại thuốc kháng sinh để xác định cơ chế tương ứng
b) So sánh các đường thể hiện hiệu quả diệt khuẩn của từng cặp loại thuốc kháng sinh với các hai cách thức khác nhau: chỉ kháng sinh và khi kết hợp với hợp chất SMX trong biểu đồ
c) So sánh các đường thể hiện hiệu quả diệt khuẩn của mỗi loại thuốc kháng sinh ở các khoảng thời gian gấp đôi nhau.
Đáp án cần chọn là: S; Đ; S