Đề thi thử đại học môn Toán đề số 49
Thời gian thi : 180 phút - Số câu hỏi : 12 câu - Số lượt thi : 229
Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"
Một số câu hỏi trong đề thi
Câu 1: Cho hàm số y=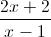 . (a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho (HS tự làm). (b) Gọi I là tâm đối xứng của đồ thị hàm số. Tìm điểm M thuộc đồ thị hàm số sao cho tiếp tuyến tại M của đồ thị hàm số cắt đường tròn tâm I bán kính 3 tại hai điểm A,B thỏa mãn AB=2
. (a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho (HS tự làm). (b) Gọi I là tâm đối xứng của đồ thị hàm số. Tìm điểm M thuộc đồ thị hàm số sao cho tiếp tuyến tại M của đồ thị hàm số cắt đường tròn tâm I bán kính 3 tại hai điểm A,B thỏa mãn AB=2
Câu 2: (cosx+1)cos2x=cos2(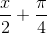 )
)
Câu 3: Giải bất phương trình:
8x+1-38.4x+14.2x+2-27>![\sqrt[3]{2^{x+1}-3}](http://images.tuyensinh247.com/picture/learning/exam/2013/1116/3496_625050_1.gif)
Câu 4: Tính tích phân: 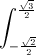
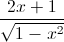 .dx
.dx
Câu 5: Cho hình trụ có chiều cao 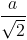 , hai đường tròn đáy là (O;a); (O';a). Điểm A thuộc đường tròn (O;a), điểm B thuộc đường tròn (O';a) sao cho AB=a. Tính thể tích của khối tứ diện OO'AB theo a.
, hai đường tròn đáy là (O;a); (O';a). Điểm A thuộc đường tròn (O;a), điểm B thuộc đường tròn (O';a) sao cho AB=a. Tính thể tích của khối tứ diện OO'AB theo a.
Câu 6: Giải hệ phương trình:
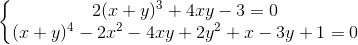
Câu 7: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giácABC có A(1;1), trực tâm H(-1;3), tâm đường tròn ngoại tiếp I(3;-3). Xác định tọa độ các đỉnh B,C biết rằng xB<xC.
Câu 8: Trong không gian với hệ tọa độ Oxyz, cho điểm A(-1;1;3), đường thẳng d1: 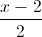 =
=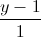 =
=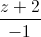 và mặt phẳng (P): x+2y+Z-3=0. Viết phương trình đường thẳng d2 đi qua điểm A biết rằng d2 cắt d1 và tạo với mặt phẳng (P) một góc 30o.
và mặt phẳng (P): x+2y+Z-3=0. Viết phương trình đường thẳng d2 đi qua điểm A biết rằng d2 cắt d1 và tạo với mặt phẳng (P) một góc 30o.
Câu 9: Giải hệ phương trình trên tập số thực: 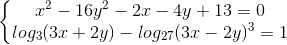
Câu 10: Trong mặt phẳng với hệ tọa độ Oxy, cho elip (E): 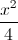 +
+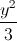 =1. Gọi F1,F2 lần lượt là hai tiêu điểm của (E). Xác định điểm M thuộc đường elip (E) sao cho M có tung độ dương và bán kính đường tròn nội tiếp của tam giác MF1F2 bằng
=1. Gọi F1,F2 lần lượt là hai tiêu điểm của (E). Xác định điểm M thuộc đường elip (E) sao cho M có tung độ dương và bán kính đường tròn nội tiếp của tam giác MF1F2 bằng 
Câu 11: Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (α) đi qua điểm I(1;-2;3) biết (α) vuông góc với mặt phẳng (β): x+2y-z+2010=0 và tạo với mặt phẳng (Oxy) một góc 45o.
Câu 12: Giải hệ phương trình: 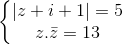 trên tập số phức
trên tập số phức
Bạn có đủ giỏi để vượt qua
| Xếp hạng | Thành viên | Đúng | Làm | Đạt | Phút |
| 1 |
|
4 | 4 | 100% | 32.4 |
| 2 |
|
3 | 5 | 60% | 17.17 |
| 3 |
|
3 | 6 | 50% | 0.92 |
| 4 |
|
3 | 8 | 38% | 1.78 |
| 5 |
|
2 | 5 | 40% | 9.2 |