Đề thi thử ĐH môn Toán lần I năm 2012-Trường THPT chuyên KHTN

Thời gian thi : 180 phút - Số câu hỏi : 9 câu - Số lượt thi : 311

Click vào đề thi   Tải đề

Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"

Một số câu hỏi trong đề thi

Câu 1: Cho hàm số y = 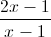\frac{2x-1}{x-1} ( C ) 1.Khảo sát sự biến thiên và vẽ đồ thị hàm số ( C ) 2.Tìm giá trị của m để đồ thị hàm số ( C ) tiếp xúc với đường thẳng y = mx + 5

Câu 2: Giải phương trình sau: cos(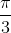\frac{\pi }{3} + 3x) + cos(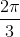\frac{2\pi }{3} - 4x) + cosx = 1

Câu 3: Tìm giá trị lớn nhất và nhỏ nhất của hàm số :    y = (3sinx + 4cosx)4(3sinx + 4cosx + 1)5

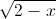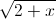Câu 4: Tìm m để phương trình sau có nghiệm thực: 9 + 2\sqrt{4-x^{2}} = m(\sqrt{2-x} + \sqrt{2+x} )

Câu 5: Tìm hệ số lớn nhất trong khai triển thành đa thức của (2x + 1)n biết tổng các hệ số của nó là 59049.

Câu 6: Cho chóp tam giác đều S.ABC biết cạnh bên bằng a, góc tạo bởi mặt bên và đáy bằng 450. Tính thể tích khối chóp.

Câu 7: Trong không gian với hệ tọa độ Oxyz, cho hình vuông ABCD có đỉnh A(1; 2; 1) và đường chéo BD có phương trình: 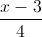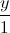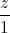\frac{x-3}{4} = - \frac{y}{1}  = \frac{z}{1}.Tìm tọa độ các đỉnh còn lại của hình vuông.

Câu 8: Trong hệ tọa độ Oxy, cho đường tròn ( C ): x2 + y2 – 2x + 2y -23 = 0. Viết phương trình đường thẳng qua A(7 ;3) cắt ( C ) tại B, C sao cho AB – 3AC = 

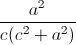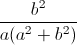Câu 9: Với a,b,c là các số thực dương thỏa mãn ab + bc + ca = 3abc. Tìm giá trị nhỏ nhất của P = \frac{a^{2}}{c(c^{2}+a^{2})} + \frac{b^{2}}{a(a^{2}+b^{2})} + \frac{c^{2}}{b(b^{2}+c^{2})}

Bạn có đủ giỏi để vượt qua

lovelyfox Pink
Xếp hạng Thành viên Đúng Làm Đạt Phút
1 Pink 8 9 89% 9.43
2 Khoảng Cách 4 4 100% 21.23
3 nguyen van hien 4 9 44% 9.42
4 Học mãi 2 9 22% 57

Cùng tham gia trao đổi với bạn bè!

Lớp 12