Đề thi thử ĐH môn Toán lần VI năm 2011-Trường THPT chuyên ĐHSPHN

Đề thi thử ĐH môn Toán lần VI năm 2011-Trường THPT chuyên ĐHSPHN

Thời gian thi : 180 phút - Số câu hỏi : 8 câu - Số lượt thi : 298

Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"

Một số câu hỏi trong đề thi

Câu 1: Cho hàm số y = x³ – 3mx² + ( m – 1)x + 2 1.Tìm m để hàm số đạt cực tiểu tại x = 2. Khảo sát sự biến thiên và vẽ đồ thị ( C ) của hàm số ứng với giá trị của m tìm được. 2.Biện luận theo k số nghiệm của phương trình x² – 2x – 2 = 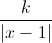$\frac{k}{|x-1|}$

Câu 2: Giải phương trình: 6sinx – 2 cos³x = 5sin2x.cosx

Câu 3: Giải hệ phương trình: $\left\{\begin{matrix}\sqrt{x-y}=9-|x+2y|\\x(x=4y-2)+y(4y+2)=41\end{matrix}\right.$

Câu 4: Tính tích phân I = 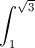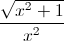$\int_{1}^{\sqrt{3}}$ $\frac{\sqrt{x^{2}+1}}{x^{2}}$ dx

Câu 5: Cho tam giác cân BMC có góc BMC = 120⁰ và đường cao MH = a√2. Trên đường thẳng vuông góc với mặt phẳng (MBC) tại M lấy hai điểm A và D về hai phía của điểm M, sao cho ABC là tam giác đều và DBC là tam giác vuông cân tại D. Tính thể tích khối cầu ngoại tiếp tứ diện ABCD.

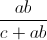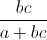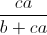Câu 6: Cho các số dương a, b, c thay đổi luôn thỏa mãn a + b + c = 1. Chứng minh rằng: $\frac{ab}{c+ab}$ + $\frac{bc}{a+bc}$ + $\frac{ca}{b+ca}$ ≥ $\frac{3}{4}$

Câu 7: Trong mặt phẳng Oxy, cho hình chữ nhật ABCD có hai giao điểm của hai đường chéo là M( $\frac{1}{2}$ ; 0), phương trình đường thẳng AB là x – 2y + 2 =0 và AB = 2AD. Tìm tọa độ các đỉnh A, B, C, D biết rằng đỉnh A có hoành độ dương.

Câu 8: Trong không gian Oxyz, cho mặt phẳng (α ): 3x + 2y – z + 4 = 0 và điểm M(2;2;0). Xác định tọa độ điểm N sao cho MN vuông góc với (α ) đồng thời N cách đều gốc tọa độ O và mặt phẳng (α ).

Bạn có đủ giỏi để vượt qua

Khoảng Cách

Xếp hạng

Thành viên

Đúng

Làm

Đạt

Phút

1	Khoảng Cách	4	5	80%	77.4
2	nunanunong	0	0	0%	4.9

Cùng tham gia trao đổi với bạn bè!

Lớp 12