Đề thi vào lớp 10 môn Toán chuyên ĐH Sư phạm TP.HCM năm 2013

Đề thi vào lớp 10 môn Toán chuyên ĐH Sư phạm TP.HCM năm 2013

Thời gian thi : 120 phút - Số câu hỏi : 13 câu - Số lượt thi : 710

Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"

Một số câu hỏi trong đề thi

Cho phương trình: x² – 2(m-3)x-2(m-1)=0 (m là tham số)

Câu 1: Chứng minh rằng phương trình luôn có 2 nghiệm phân biệt với mọi m.

Câu 2: Gọi x₁, x₂ là 2 nghiệm của phương trình .Hãy tìm các giá trị của m thỏa mãn: 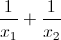$\frac{1}{x_{1}}+\frac{1}{x_{2}}$ = x₁+x₂

Cho hàm số : y = 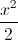$\frac{x^{2}}{2}$ (P) và hàm số: y= x - $\frac{1}{2}$ (D)

Câu 3: Vẽ (P) và (D) trên cùng một mặt phẳng tọa độ Oxy.

Câu 4:

Giải

Câu 5: Rút gọn biểu thức; M = 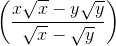$\left ( \frac{x\sqrt{x}-y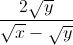\sqrt{y}}{\sqrt{x}-\sqrt{y}} \right )$ :(x-y) - $\frac{2\sqrt{y}}{\sqrt{x}-\sqrt{y}}$ với x>0; y>0, x 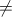$\neq$ y

Câu 6: Người ta làm một vườn hoa gồm 2 hình tròn tâm A và B tiếp xúc ngoài với nhau. Biết AB = 5cm và diện tích vườn hoa là 13,48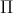 $\Pi$ m ². Tính bán kính của mỗi hình tròn.

Câu 7: Giải hệ phương trình: 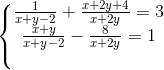$\left\{\begin{matrix} \frac{1}{x+y-2}+\frac{x+2y+4}{x+2y}=3\\ \frac{x+y}{x+y-2}-\frac{8}{x+2y} = 1 \\ \\ \end{matrix}\right.$

Cho tam giác ABC vuông tại A (AB<AC), có đường cao AH và O là trung điểm BC. Đường tròn tâm I đường kính AH cắt AB, AC lần lượt tại M và N.

Câu 8: Chứng minh rằng : AM.AB=AN.ACBMNC nội tiếp.

Câu 9: Chứng minh rằng: Tứ giác BMNC nội tiếp.

Câu 10: Gọi D là giao điểm của OA và MN. Chứng minh rằng: Tư giác ODIH nội tiếp.

Câu 11: Chứng minh 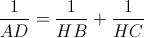$\frac{1}{AD}=\frac{1}{HB}+\frac{1}{HC}$

Câu 12: Gọi P là giao điểm của MN và BC. Đường thẳng AP cắt đường tròn đường kính AH tại K( khác A). Tính 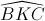$\widehat{BKC}$ .

Câu 13:

Bạn có đủ giỏi để vượt qua

Lê Ngọc Anh

Xếp hạng

Thành viên

Đúng

Làm

Đạt

Phút

1	Lê Ngọc Anh	9	11	82%	41.67
2	Vũ Lạc Hoan	8	11	73%	19.33
3	NGUYEN THANH DAT	3	11	27%	2.3
4	Thái Thị Thanh Nga	9	11	82%	40.02
5	Linh Linh'ss	3	11	27%	1.37
6	nguyen khanh hung	1	1	100%	0.75
7	Danh Tuấn	4	10	40%	1.13
8	Vũ Việt Hoài	0	0	0%	1.2
9	Baokute Nhontho	1	11	9%	0.32

Cùng tham gia trao đổi với bạn bè!

Lớp 9