Đề thi vào lớp 10 môn Tóan chuyên thành phố Hồ Chí Minh năm 2011
Thời gian thi : 120 phút - Số câu hỏi : 10 câu - Số lượt thi : 777
Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"
Một số câu hỏi trong đề thi
Câu 1: Giải phương trình sau: (x2 – 4x)2 – 4(x – 2)2 + 19 = 0
Câu 2: Giải hệ phương trình: 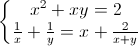
Trong hệ trục tọa độ Oxy, cho parabol (P): y =  x2 và đường thẳng (d): mx – y + 1 = 0 (m là tham số)
x2 và đường thẳng (d): mx – y + 1 = 0 (m là tham số)
Câu 3: Chứng tỏ (d) luôn cắt (P) tại hai điểm phân biệt A và B.
Câu 4: Định m để tam giác AOB có diện tích bằng  .
.
Câu 5: Tìm đa thức dư khi chia x6 cho x2 – x – 1
Câu 6: Giả sử x1, x2 là hai nghiệm của phương trình x2 – x – 1 = 0 . Tính giá trị của biểu thức : A = (x12011 – x12012 + x12008 + x12009 + x16 – 5 + x2)(x22011 – x22012 + x22008 + x26 – 5 + x1)
Câu 7: Tìm các số nguyên x, y thỏa : 5x2 + y2 – 2xy + 2x – 6y + 1 < 0
Câu 8: Cho tam giác ABC cân tại A nội tiếp đường tròn (O). Từ điểm D trên cung nhỏ AB của đường tròn (O), ta kẻ đường thẳng vuông góc với AD, đường thẳng này cắt cạnh BC tại M. Đường trung trực của DM cắt các cạnh AB, AC lần lượt tại E và F. Chứng minh AEMF là hình bình hành.
Câu 9: Cho tam giác ABC có hai đường phân giác trong BD và CE . M là một điểm bất kì trên đoạn DE. Gọi H, K, L lần lượt là hình chiếu của M trên các cạnh BC, CA, A. Chứng minh MH = MK + ML.
Câu 10: Cho a, b, c là ba số dương thỏa mãn điều kiện ab + bc + ca = 1. Tìm giá trị nhỏ nhất của biểu thức : P = 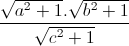 +
+ 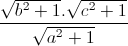 +
+ 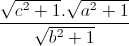
Bạn có đủ giỏi để vượt qua
| Xếp hạng | Thành viên | Đúng | Làm | Đạt | Phút |
| 1 |
|
4 | 10 | 40% | 7.02 |
| 2 |
|
2 | 4 | 50% | 15.98 |
| 3 |
|
1 | 10 | 10% | 0.75 |
| 4 |
|
2 | 10 | 20% | 11.87 |
| 5 |
|
2 | 10 | 20% | 2.13 |
| 6 |
|
0 | 0 | 0% | 0.78 |
| 7 |
|
4 | 10 | 40% | 4.68 |
| 8 |
|
1 | 10 | 10% | 1.07 |
| 9 |
|
0 | 0 | 0% | 0.42 |
| 10 |
|
0 | 0 | 0% | 1.65 |
| 11 |
|
2 | 7 | 29% | 0.37 |
| 12 |
|
3 | 10 | 30% | 0.17 |
| 13 |
|
2 | 10 | 20% | 5.23 |
| 14 |
|
1 | 10 | 10% | 0.28 |