Cho tứ diện đều \(ABCD\) có tất cả các cạnh đều bằng \(2a\). Khoảng cách từ đỉnh \(A\) đến mặt phẳng \(\left( {BCD} \right)\) bằng

Câu 548106: Cho tứ diện đều \(ABCD\) có tất cả các cạnh đều bằng \(2a\). Khoảng cách từ đỉnh \(A\) đến mặt phẳng \(\left( {BCD} \right)\) bằng

A. \(\dfrac{{2\sqrt 6 a}}{3}\).

B. \(\dfrac{{a\sqrt 6 }}{3}\).

C. \(\dfrac{{4\sqrt 6 a}}{3}\).

D. \(\dfrac{{a\sqrt {33} }}{3}\).

Câu hỏi : 548106

Phương pháp giải:

Sử dụng tính chất của tứ diện đều \(ABCD\), có \(O\) là tâm đáy thì \(AO \bot \left( {BCD} \right)\,\, \Rightarrow d\left( {A;\,\,\left( {BCD} \right)} \right) = AO\).

Đáp án : A
(0) bình luận (0) lời giải
Giải chi tiết:
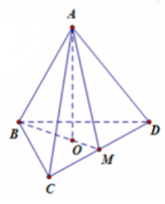
Gọi \(O\) là tâm của \(\Delta BCD,\,\,M\) là trung điểm \(CD\).
Vì tứ diện \(ABCD\) đều nên \(AO \bot \left( {BCD} \right)\,\, \Rightarrow d\left( {A;\,\,\left( {BCD} \right)} \right) = AO\).
\(BM = \,\dfrac{{2a\sqrt 3 }}{2} = a\sqrt 3 ;\,\,BO = \,\dfrac{2}{3}BM = \,\,\dfrac{{2a\sqrt 3 }}{3}\);
\(AO = \,\sqrt {A{B^2} - B{O^2}} = \,\sqrt {4{a^2} - \dfrac{{12{a^2}}}{9}} = \,\dfrac{{2a\sqrt 6 }}{3}\)

Lời giải sai Bình thường Khá hay Rất Hay
- Mẹo : Viết lời giải với bộ công thức đầy đủ tại đây

Xem bình luận

2K7 tham gia ngay group để nhận thông tin thi cử, tài liệu miễn phí, trao đổi học tập nhé!

>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.