Đề thi Cao đẳng môn Toán khối A, B, D năm 2009
Thời gian thi : 180 phút - Số câu hỏi : 12 câu - Số lượt thi : 546
Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"
Một số câu hỏi trong đề thi
Câu 1: Cho hàm số y = x3 – (2m – 1)x2 + (2 – m)x + 2 (1), với m là tham số thực. 1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1) khi m = 2. 2. Tìm các giá trị của m để hàm số (1) có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số (1) có hoành độ dương
Câu 2: Giải phương trình (1 + 2 sin x)2 cos x = 1 + sin x + cos x.
Câu 3: Giải bất phương trình: 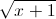 + 2
+ 2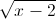 ≤
≤ 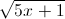 (x ∈ R)
(x ∈ R)
Câu 4: Tính tích phân: I = 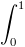 (e-2x + x)ex dx
(e-2x + x)ex dx
Câu 5: Cho hình chóp tứ giác đều S.ABCD có AB = a, SA = a√2 . Gọi M , N và P lần lượt là trung điểm của các cạnh SA, SB và CD. Chứng minh rằng đường thẳng MN vuông góc với đường thẳng SP. Tính theo a thể tích của khối tứ diện AMNP
Câu 6: Cho a và b là hai số thực thỏa mãn 0 < a < b < 1. Chứng minh rằng a2 ln b – b2 ln a > ln a – ln b
Câu 7: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có C (−1; − 2), đường trung tuyến kẻ từ A và đường cao kẻ từ B lần lượt có phương trình là 5x + y − 9 = 0 và x + 3 y − 5 = 0. Tìm tọa độ các đỉnh A và B.
Câu 8: Trong không gian với hệ tọa độ Oxyz, cho các mặt phẳng (P1) : x + 2y + 3z + 4 = 0 và (P2) : 3x + 2 y − z + 1 = 0. Viết phương trình mặt phẳng (P) đi qua điểm A(1; 1; 1), vuông góc với hai mặt phẳng (P1) và (P2)
Câu 9: Cho số phức z thỏa mãn (1 + i)2 (2 – i)z = 8 + i + (1 + 2i)z. Tìm phần thực và phần ảo của z.
Câu 10: Trong mặt phẳng với hệ tọa độ Oxy, cho các đường thẳng ∆1: x - 2y - 3 = 0 và ∆2: x + y + 1 = 0. Tìm tọa độ điểm M thuộc đường thẳng ∆1 sao cho khoảng cách từ điểm M đến đường thẳng ∆2 bằng 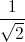 .
.
Câu 11: Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(1; 1; 0), B(0; 2; 1) và trọng tâm G(0; 2; −1). Viết phương trình đường thẳng Δ đi qua điểm C và vuông góc với mặt phẳng ( ABC ).
Câu 12: Giải phương trình sau trên tập hợp các số phức: 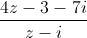 = z - 2i
= z - 2i
Bạn có đủ giỏi để vượt qua
| Xếp hạng | Thành viên | Đúng | Làm | Đạt | Phút |
| 1 |
|
7 | 8 | 88% | 54.75 |
| 2 |
|
7 | 8 | 88% | 34.42 |
| 3 |
|
6 | 7 | 86% | 180.97 |
| 4 |
|
6 | 9 | 67% | 49.3 |
| 5 |
|
4 | 6 | 67% | 77.45 |
| 6 |
|
1 | 1 | 100% | 7.23 |
| 7 |
|
0 | 1 | 0% | 29.83 |
| 8 |
|
0 | 0 | 0% | 8.6 |
| 9 |
|
2 | 8 | 25% | 1.32 |
| 10 |
|
0 | 0 | 0% | 0.05 |
| 11 |
|
2 | 5 | 40% | 1.32 |
| 12 |
|
0 | 0 | 0% | 0.53 |
| 13 |
|
2 | 8 | 25% | 0.22 |
| 14 |
|
1 | 9 | 11% | 0.4 |