Đề thi thử đại học môn toán đề số 19
Thời gian thi : 180 phút - Số câu hỏi : 8 câu - Số lượt thi : 222
Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"
Một số câu hỏi trong đề thi
Câu 1: Cho hàm số y =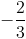 
x3 + (m – 1) + (3m – 2)x - 
có đồ thị (Cm) với m là tham số thực. 1. Khảo sát sự biến thiên và vẽ đồ thị (Cm) của hàm số m = 2. 2. Tìm m để trên (Cm) có hai điểm phân biệt M1(x1;y1), M(x2;y2) thỏa mãn x1;x2 >0 và tiếp tuyến của (Cm) tại mỗi điểm đó vuông góc với đường thẳng d: x – 3y + 1 = 0
Câu 2: Giải bất phương trình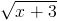 
+ x2 + x ≤ 2 +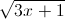 
Câu 3: Cho hình lăng trụ ABC.A'B'C' có đấy là tam giác vuông cân, AB = AC = a. Hình chiếu của B xuống (A'B'C') trùng với trung điểm của B'C'. Gọi M là trung điểm của A'C'. Tính thể tích khối lăng trụ ABC.A'B'C' và góc giữa hai đường thẳng BC' và MB' biết rằng AA' = a.
Câu 4: Cho các số thực dương a, b, c. Tìm giá trị lớn nhất của biểu thức P =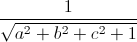 
- 
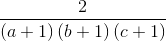
Câu 5: Trong mặt phẳng với hệ trục Oxy, cho đường tròn (C): (x – 1)2 + (y + 2)2 = 4. Tìm các điểm A, B, C nằm trên đường tròn (C) biết rằng điểm B có hoành độ dương AB = BC và M(0; -1) là trung điểm cạnh BC
Câu 6: Trong không gian với hệ tọa độ Oxyz, cho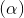 
: 3x + 2y - z + 4 = 0, I(2; 2; 0). Tìm tọa độ điểm M biết rằng MI ⊥ 
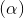, đồng thời M cách đều gốc tọa độ và mặt phẳng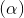 
Câu 7: Trong kỳ thi tuyển sinh đại học, trường A có 5 học sinh gồm 3 nam và 2 nữ cùng đậu vào khoa X của một trường đại học. Số sinh viên đậu vào khoa X được chia ngẫu nhiên thành 4 lớp. Tính xác suất để có một lớp có đúng 2 nam và 1 nữ của trường A
Câu 8: Trong mặt phẳng với hệ trục Oxy, cho đường thẳng ∆: x - y = 0 và đường tròn (C): x2 + y2 + 2x – 6y + 6 = 0. Từ một điểm M bất kỳ trên ∆ kẻ hai tiếp tuyến MA, MB đến đường tròn (C) (A và B là hai tiếp điểm). Tìm M để đường thẳng AB đi qua điểm E(0; -1).
