Đề thi thử đại học môn Toán đề số 26
Thời gian thi : 180 phút - Số câu hỏi : 12 câu - Số lượt thi : 167
Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"
Một số câu hỏi trong đề thi
Câu 1: Cho hàm số y = x3 – 3x2 + 2 (a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho (HS tự làm) . (b) Viết phương trình tiếp tuyến d của (C) biết rằng d cắt các trục Ox,Oy lần lượt tại các điểm phân biệt A,b sao cho OB = 9OA
Câu 2: Giải phương trình: (1 + sin2x)cosx + (1 + cos2x)sinx = 1 + sin2x.
Câu 3: Giải hệ phương trình: 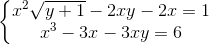 (x,y∈ R)
(x,y∈ R)
Câu 4: Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số y=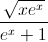 , trục hoành và đường thẳng x=1 xung quanh trục hoành.
, trục hoành và đường thẳng x=1 xung quanh trục hoành.
Câu 5: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, tam giác SCD vuông tại S, góc 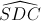 = 30o , hình chiếu của S xuống (ABCD) nằm trên cạnh CD. Gọi M là trung điểm của SA. Tính thể tích khối chóp MABD và góc giữa hai đường thẳng AC và DM.
= 30o , hình chiếu của S xuống (ABCD) nằm trên cạnh CD. Gọi M là trung điểm của SA. Tính thể tích khối chóp MABD và góc giữa hai đường thẳng AC và DM.
Câu 6: Cho các số thực dương a,b,c thỏa mãn điều kiện |a-b|+|b-c|+|c-a|+3.![\sqrt[3]{abc}](http://images.tuyensinh247.com/picture/learning/exam/2013/1108/1097_734_1.gif) = 1. Chứng minh rằng: a
= 1. Chứng minh rằng: a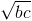 + b
+ b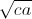 + c
+ c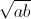 ≤
≤  .
.
Câu 7: Trong mặt phẳng với hệ trục Oxy, cho hình thoi ABCD có A(5;5), đưởng thẳng đi qua trung điểm BC và CD có phương trình ∆: x + y + 14 = 0, điểm E(0;4) nằm trên đường thẳng đi qua D và vuông góc với AB. Tìm tọa độ các đỉnh còn lại của hình thoi đã cho.
Câu 8: Trong không gian với hệ tọa độ Oxyz, cho điểm I(1;1;1) và đường thẳng d: 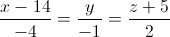 . Viết phương trình mặt cầu (S) tâm I và cắt đường thẳng d tại điểm A và B sao cho AB=16
. Viết phương trình mặt cầu (S) tâm I và cắt đường thẳng d tại điểm A và B sao cho AB=16
Câu 9: Trong mặt phẳng tọa độ, giả sử điểm A biểu diễn nghiệm z1 của phương trình z2-2z+5=0 và điểm B biểu diễn số phức z2=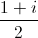 z1. Tính diện tích tam giác OAB (O là gốc tọa độ).
z1. Tính diện tích tam giác OAB (O là gốc tọa độ).
Câu 10: Trong mặt phẳng với hệ trục Oxy, cho tam giác ABC vuông tại A. Điểm M (2;6) nằm trên đường thẳng AB, điểm I(7;3) là trung điểm của BC. Gọi N là điểm đối xứng với trung điểm của AB qua I. Biết rằng N nằm trên đường thẳng ∆: x+y-7=0 Viết phương trình cạnh AB.
Câu 11: Trong không gian với hệ tọa độ Oxyz, cho: (P): x - 2y + 2z + 1 = 0 cắt mặt cầu (S): (x - 2)2 + (y + 3)2 + (z + 3)2 = 5 theo giao tuyến là đường tròn (C). Viết phương trình mặt cầu (S’) có tâm thuộc (α): x + y + z + 3 = 0 và chứa đường tròn (C) nói trên
Câu 12: Giải hệ phương trình 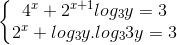 (x,y∈R)
(x,y∈R)
Bạn có đủ giỏi để vượt qua
| Xếp hạng | Thành viên | Đúng | Làm | Đạt | Phút |
| 1 |
|
7 | 7 | 100% | 26.3 |
| 2 |
|
7 | 7 | 100% | 97.28 |
| 3 |
|
1 | 1 | 100% | 15.53 |
| 4 |
|
0 | 0 | 0% | 1.7 |
| 5 |
|
2 | 9 | 22% | 0.38 |