Đề thi thử đại học môn Toán đề số 9
Thời gian thi : 180 phút - Số câu hỏi : 11 câu - Số lượt thi : 184
Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"
Một số câu hỏi trong đề thi
Câu 1: Cho hàm số y = 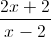 a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. (HS tự làm). (b) Tìm m để đường thẳng d: y = mx+1 cắt (C) tại hai điểm phân biệt sao cho tiếp tuyến của (C) tại hai điểm đó song song với nhau.
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. (HS tự làm). (b) Tìm m để đường thẳng d: y = mx+1 cắt (C) tại hai điểm phân biệt sao cho tiếp tuyến của (C) tại hai điểm đó song song với nhau.
Câu 2: Giải phương trình 2tanx + sin(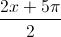 ) =
) = ![]() .
.
Câu 3: Giải hệ phương trình ![\left\{\begin{matrix}x^{2}+\sqrt{x+2}=y^{2}+\sqrt{3-y}\\x^{3}+\sqrt[3]{x+2y}=y^{3}+\sqrt[3]{y}\end{matrix}\right.](http://images.tuyensinh247.com/picture/learning/exam/2013/1111/1761_769_1.gif) (x,y
(x,y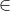
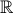 )
)
Câu 4: Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số y = 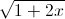 .e3x và các trục tọa độ xung quanh trục hoành.
.e3x và các trục tọa độ xung quanh trục hoành.
Câu 5: Cho các số thực dương x, y, z thỏa mãn điều kiện x + y + z = 3. Chứng minh rằng 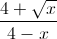 +
+ 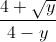 +
+ 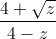 ≥ 5
≥ 5
Câu 6: Trong mặt phẳng với hệ trục Oxy, cho tam giác ABC có M(2;3) là trung điểm AB, H (1;5), K(5;9) lần lượt là chân đường cao kẻ từ C và B. Tìm tọa độ 3 đỉnh A,B,C biết đỉnh B có hoành độ dương.
Câu 7: Trong không gian với hệ tọa độ Oxyz, cho (P) : 2x + y -z =0, d: 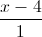 =
= 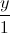 =
= 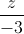 , ∆:
, ∆: 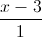 =
= 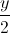 =
= 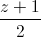 . Tìm tọa độ điểm M nằm trên (P), điểm N trên đường thẳng d sao cho M và N đối xứng với nhau qua đường thẳng ∆.
. Tìm tọa độ điểm M nằm trên (P), điểm N trên đường thẳng d sao cho M và N đối xứng với nhau qua đường thẳng ∆.
Câu 8: An và Bình thi đấu với nhau một trận bóng bàn, người nào thắng trước 3 séc thì thắng trận. Xác suất An thắng mỗi séc là 0,4 (không có hòa). Tính xác suất An thắng trận.
Câu 9: Trong mặt phẳng với hệ trục Oxy, cho hình vuông ABCD có BD: x + 2y = 0, đỉnh A thuộc đường thẳng d: x - y - 2 =0, đường thẳng CD đi qua điểm M(6;-8). Tìm tọa độ tâm I của hình vuông.
Câu 10: Trong không gian với hệ tọa độ Oxyz, cho (P) ; 2x + y -z =0, d: 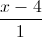 =
= 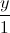 =
= 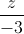 và M (1;-1;1). Viết phương trình đường thẳng ∆ đi qua M, vuông góc với đường thẳng d và tạo với (P) một góc bằng 300 .
và M (1;-1;1). Viết phương trình đường thẳng ∆ đi qua M, vuông góc với đường thẳng d và tạo với (P) một góc bằng 300 .
Câu 11: Tìm số phức z thỏa mãn |1 - 2z| = |i - 2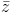 | và
| và 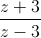 có một acgumen bằng
có một acgumen bằng 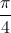
Bạn có đủ giỏi để vượt qua
| Xếp hạng | Thành viên | Đúng | Làm | Đạt | Phút |
| 1 |
|
6 | 6 | 100% | 129.02 |
| 2 |
|
4 | 6 | 67% | 40.88 |