Đề thi thử đại học môn Toán lần III năm 2012 - trường THPT chuyên ĐHSP Hà Nội

Thời gian thi : 180 phút - Số câu hỏi : 8 câu - Số lượt thi : 291

Click vào đề thi   Tải đề

Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"

Một số câu hỏi trong đề thi

Câu 1: Cho hàm số y=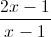\frac{2x-1}{x-1}. 1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (học sinh tự giải) 2. Gọi I là giao điểm hai đường tiệm cận của (C). Với giá trị nào của m, đường thẳng y=-x+m cắt (C) tại hai điểm phân biệt A,B và tam giác IAB đều.

Câu 2: a. Cho các số dương a,b,c,m,n,p thỏa mãn a+m=b+n=c+p=k Chứng minh rằng: an+bp+cm<k2 b. Tìm các giá trị của tham số a để phương trình sau có đúng 2 nghiệm phân biệt: log3x2+a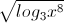\sqrt{log_{3}x^{^{8}}}+a+1=0

Câu 3: Tính tích phân: 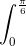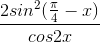\int_{0}^{\frac{\pi }{6}}\frac{2sin^{2}(\frac{\pi }{4}-x)}{cos2x}dx

Câu 4: Tứ diện ABCD có cạnh AB=6, cạnh CD=8 và các cạnh còn lại bằng 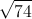\sqrt{74}. Hãy tính diện tích mặt cầu ngoại tiếp tứ diện ABCD

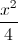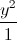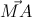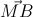
Câu 5: Cho điểm M(0;2) và hypebol (H): \frac{x^{2}}{4}-\frac{y^{2}}{1}=1.Lấp phương trình đường thẳng (d) đi qua điểm M cắt (H) tại hai điểm phân biệt A,B sao cho \vec{MA}=\frac{5}{3}\vec{MB}

Câu 6: Trong không gian Oxyz cho mặt cầu (S): x2+y2+z2+6x-2y-2z-14=0.viết phương trình mặt phẳng (P) chứa trục Oz cắt mặt cầu theo một đường tròn có bán kính r=4

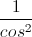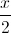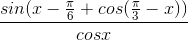
Câu 7: \frac{1}{cos^{2}} - (cosx+sinx.tan\frac{x}{2})= \frac{sin(x-\frac{\pi }{6}+cos(\frac{\pi }{3}-x))}{cosx}

Câu 8: Giải hệ bất phương trình: 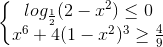\left\{\begin{matrix} log_{\frac{1}{2}}(2-x^{2})\leq 0\\x^{6}+4(1-x^{2})^{3}\geq \frac{4}{9} \end{matrix}\right.

Bạn có đủ giỏi để vượt qua

nguyennhuthoa nguyennhuthoa
Xếp hạng Thành viên Đúng Làm Đạt Phút
1 nguyennhuthoa 3 3 100% 124.23
2 nunanunong 2 2 100% 34.85
3 phamtan 2 3 67% 23.35
4 jaybui 1 1 100% 37.32
5 Bích Ngọc 0 0 0% 0.93
6 phamduytan 1 4 25% 12.18
7 Nhi Yến 0 1 0% 14.9
8 Quang Lâm 2 8 25% 5.07
9 Nguyễn Thành Tâm 2 8 25% 0.12
10 lavender nguyen 1 8 13% 5.92

Cùng tham gia trao đổi với bạn bè!

Lớp 12