Đề thi vào lớp 10 môn Toán TPHCM năm 2013

Thời gian thi : 120 phút - Số câu hỏi : 14 câu - Số lượt thi : 703

Click vào đề thi  

Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"

Một số câu hỏi trong đề thi

Giải các phương trình và hệ phương trình sau:

Câu 1: 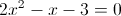2x^{2}-x-3=0

Câu 2: 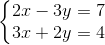\left\{\begin{matrix} 2x-3y=7\\ 3x+2y=4 \end{matrix}\right.

Câu 3: 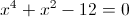x^{4}+x^{2}-12=0

Câu 4: 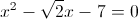x^{2}-\sqrt{2}x-7=0

Cho ham số y = 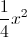\frac{1}{4}x^{2} và đường thẳng (D): y=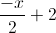 \frac{-x}{2}+2

Câu 5: Vẽ đồ thị (P) và đường thẳng (D).

Câu 6: Tìm tọa độ các giao điểm của (P) và (D).

Cho đường tròn (O) có tâm O và điểm M nằm ngoài đường tròn (O). Đường thẳng MO cắt (O) tại E và F (ME<MF). Vẽ cát tuyến MAB và tiếp tuyến MC của (O) (C là tiếp điểm , A nằm giữa hai điểm M và B, A và C nằm khác phía với đường thẳng MO)

Câu 7: Chứng minh rằng : MA.MB=ME.MF

Câu 8: Gọi H là hình chiếu vuông góc của điểm C lên đường thằng MO.Chứng minh tứ giác AHOB nội tiếp.

Câu 9: Trên nửa mặt phẳng bờ OM có chứa điểm A, vẽ nửa đường tròn đường kính  MF; nửa đường tròn này cắt tiếp tuyến tại E của (O) ở K.Gọi S là giao điểm của hai đường thẳng CO và KF.Chứng minh rằng đường thẳng MS vuông góc với đường thẳng KC.

Câu 10: Gọi P và Q lần lượt là tâm đường tròn ngoại tiếp tam giác EFS và ABS và T là trung điểm của KS. Chúng minh ba điểm P,Q,T thẳng hàng.

Thu gọn biểu thức sau:

Câu 11: A = 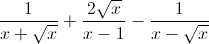\frac{1}{x+\sqrt{x}}+\frac{2\sqrt{x}}{x-1}-\frac{1}{x-\sqrt{x}}  với x>0; x 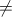\neq 1

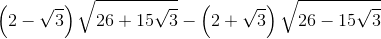
Câu 12: B= \left ( 2-\sqrt{3} \right )\sqrt{26+15\sqrt{3}}-\left ( 2+\sqrt{3} \right )\sqrt{26-15\sqrt{3}}  

Cho phương trình: 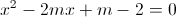x^{2}-2mx+m-2=0 ( x là ẩn số)

Câu 13: Chứng minh rằng  phương trình luôn có hai nghiệm phân biệt với mọi m.

Câu 14: Gọix1, x2 là các nghiệm  của phương trình . Tìm m để biểu thức M = 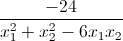\frac{-24}{x_{1}^{2}+x_{2}^{2}-6x_{1}x_{2}} đạt giá trị nhỏ nhất.

Bạn có đủ giỏi để vượt qua

daigiahuong99 abcdefghik
Xếp hạng Thành viên Đúng Làm Đạt Phút
1 abcdefghik 9 14 64% 4.28
2 Nguyệt Hà 6 14 43% 9.27
3 Mèo Ác 5 14 36% 16.4
4 Tấn Khoa 13 14 93% 31.98
5 Thảo Vân 5 14 36% 6.28
6 Nguyễn Bùi Nhật Quyên 8 14 57% 45.03
7 Hưng Phạm 10 14 71% 31.6
8 Tuấn Nguyễn 4 14 29% 7.67
9 Phạm Tứ Đạt 7 12 58% 46.58
10 Miu'ss Nhõ'ss 6 14 43% 4.38
11 Triệu Vy 1 2 50% 4.82
12 Danh Tuấn 12 14 86% 26.77
13 Minh Lê 7 13 54% 31.78
14 Nguyễn Huỳnh Hoàng Duy 6 13 46% 5.62
15 Cao Văn Minh 12 12 100% 17.13
16 huynh tan phat 5 14 36% 3.72
17 Linh Linh'ss 5 14 36% 5.55
18 Cao Ha Minh 11 13 85% 5.23

Cùng tham gia trao đổi với bạn bè!

Lớp 9