Đề thi Cao đẳng môn Toán khối A, A1,B, D năm 2012
Thời gian thi : 180 phút - Số câu hỏi : 12 câu - Số lượt thi : 686
Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"
Một số câu hỏi trong đề thi
Câu 1: Cho hàm số y = 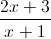 (1).a)Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1),b)Viết phương trình tiếp tuyến d của đồ thị hàm số (1), biết rằng d vuông góc với đường thẳng y = x + 2.
(1).a)Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1),b)Viết phương trình tiếp tuyến d của đồ thị hàm số (1), biết rằng d vuông góc với đường thẳng y = x + 2.
Câu 2: Giải phương trình 2cos2x + sinx = sin3x.
Câu 3: Giải bất phương trình log2(2x).log3(3x) > 1.
Câu 4: Tính tích phân I = 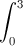
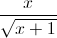 dx.
dx.
Câu 5: Cho khối chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = a√2, SA = SB = SC. Góc giữa đường thẳng SA và mặt phẳng (ABC) bằng 600. Tính thể tích khối chóp S.ABC và bán kính mặt cầu ngoại tiếp hình chóp S.ABC theo a.
Câu 6: Giải phương trình 4x3 + x – (x + 1)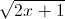 = 0 (x ∈ R).
= 0 (x ∈ R).
Câu 7: Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C ): x2 + y2 – 2x – 4y + 1 = 0 và đường thẳng d: 4x – 3y + m = 0. Tìm m để d cắt (C) tại hai điểm A, B sao cho 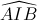 = 1200, với I là tâm của (C).
= 1200, với I là tâm của (C).
Câu 8: Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng : d1 : 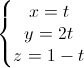 (t ∈ R) , d2:
(t ∈ R) , d2: 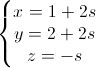 (s ∈ R).
(s ∈ R).
Chứng minh d1 và d2 cắt nhau. Viết phương trình mặt phẳng chứa hai đường thẳng d1, d2.
Câu 9: Cho số phức z thỏa mãn (1 – 2i)z - 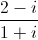 = (3 – i)z. Tìm tọa độ điểm biểu diễn của z trong mặt phẳng tọa độ Oxy.
= (3 – i)z. Tìm tọa độ điểm biểu diễn của z trong mặt phẳng tọa độ Oxy.
Câu 10: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC. Các đường thẳng BC, BB’, B’C’ lần lượt có phương trình là y – 2 = 0, x – y + 2 = 0, x – 3y + 2 = 0; với B’, C’ tương ứng là chân các đường cao kẻ từ B, C của tam giác ABC. Viết phương trình các đường thẳng AB, AC.
Câu 11: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: 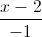 =
= 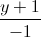 =
= 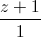 và mặt phẳng (P) : 2x + y – 2z = 0. Đường thẳng ∆ nằm trong (P) vuông góc với d tại giao điểm của d và (P). Viết phương trình đường thẳng ∆ .
và mặt phẳng (P) : 2x + y – 2z = 0. Đường thẳng ∆ nằm trong (P) vuông góc với d tại giao điểm của d và (P). Viết phương trình đường thẳng ∆ .
Câu 12: Gọi z1, z2 là hai nghiệm phức của phương trình z2 – 2z + 1 + 2i = 0 . Tính |z1| + |z2|.
Bạn có đủ giỏi để vượt qua
| Xếp hạng | Thành viên | Đúng | Làm | Đạt | Phút |
| 1 |
|
9 | 9 | 100% | 42.38 |
| 2 |
|
9 | 9 | 100% | 52.67 |
| 3 |
|
8 | 9 | 89% | 4.68 |
| 4 |
|
8 | 9 | 89% | 7.7 |
| 5 |
|
7 | 9 | 78% | 78.27 |
| 6 |
|
5 | 5 | 100% | 0.47 |
| 7 |
|
6 | 9 | 67% | 42.97 |
| 8 |
|
5 | 6 | 83% | 178.63 |
| 9 |
|
4 | 5 | 80% | 91.13 |
| 10 |
|
4 | 5 | 80% | 29.92 |
| 11 |
|
4 | 7 | 57% | 29.57 |
| 12 |
|
3 | 4 | 75% | 48.68 |
| 13 |
|
3 | 4 | 75% | 40.77 |
| 14 |
|
2 | 2 | 100% | 6.17 |
| 15 |
|
2 | 2 | 100% | 9.98 |
| 16 |
|
4 | 8 | 50% | 0.22 |
| 17 |
|
3 | 6 | 50% | 7.17 |
| 18 |
|
4 | 9 | 44% | 77.78 |
| 19 |
|
4 | 9 | 44% | 6.02 |
| 20 |
|
2 | 4 | 50% | 15.02 |
| 21 |
|
1 | 1 | 100% | 20.9 |
| 22 |
|
1 | 1 | 100% | 12.33 |
| 23 |
|
2 | 4 | 50% | 6.95 |
| 24 |
|
1 | 2 | 50% | 7.33 |
| 25 |
|
0 | 0 | 0% | 0.88 |
| 26 |
|
3 | 9 | 33% | 1.03 |
| 27 |
|
1 | 3 | 33% | 5.48 |
| 28 |
|
1 | 4 | 25% | 8.35 |
| 29 |
|
2 | 9 | 22% | 2.78 |
| 30 |
|
1 | 8 | 13% | 1.98 |