Đề thi thử đại học môn Toán đề số 51
Thời gian thi : 180 phút - Số câu hỏi : 12 câu - Số lượt thi : 244
Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"
Một số câu hỏi trong đề thi
Câu 1: Cho hàm số: y=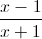 (a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (HS tự làm). (b) Tìm a,b để đường thẳng (d): y=ax+b cắt (C) tại hai điểm phân biệt đối xứng nhau qua đường thẳng (∆): x-2y+3=0.
(a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (HS tự làm). (b) Tìm a,b để đường thẳng (d): y=ax+b cắt (C) tại hai điểm phân biệt đối xứng nhau qua đường thẳng (∆): x-2y+3=0.
Câu 2: Giải phương trình:
(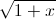 -1)(
-1)(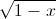 +1)=2x
+1)=2x
Câu 3: Giải hệ phương trình:
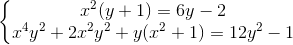
Câu 4: Tính tích phân: 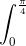
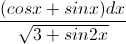
Câu 5: Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình thoi cạnh a , góc giữa mặp phẳng (A’BD) và mặt phẳng đáy bằng 60o. Tính Vhộp và tính theo a khoảng cách giữa đường thẳng CD’ và mặt phẳng (A’BD)
Câu 6: Cho x,y,z là 3 số dương thỏa mãn: xy+yz+zx=3 Chứng minh: 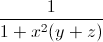 +
+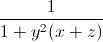 +
+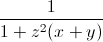 ≤
≤ 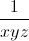 Dấu "=" xảy ra khi:
Dấu "=" xảy ra khi:
Câu 7: Trong không gian Oxyz cho đường thẳng d có phương trình: 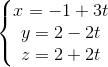 và cho điểm A(1;2;-1); B(7;-2;3) Tìm điểm I thuộc đường thẳng d sao cho: IA+IB nhỏ nhất
và cho điểm A(1;2;-1); B(7;-2;3) Tìm điểm I thuộc đường thẳng d sao cho: IA+IB nhỏ nhất
Câu 8: Trong mặt phẳng với hệ tọa độ Oxy cho A(-1;1), B(3;3) và đường thẳng d: 3x-4y+8=0. Lập phương trình đường tròn qua A, B và tiếp xúc với d.
Câu 9: Tính tổng S= 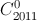 -
-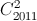 +
+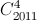 -...-
-...-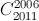 +
+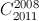 -
-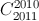
Câu 10: Trong mặt phẳng Oxy lập phương trình chính tắc Hypebol (H) đi qua A(6;3) và có góc giữa 2 tiệm cận của nó bằng 60o.
Câu 11: Trong không gian với hệ tọa độ Oxyz cho A(2;0;0), M(1;1;1). Giả sử (P) là mặt phẳng thay đổi nhưng luôn qua đường thẳng đường thằng AM và cắt các trục Oy,Oz lần lượt tại B(0;b;0), C(0;0;c) với b,c>0 Chứng minh: b+c=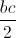 và tìm b,c để S∆ABC nhỏ nhất
và tìm b,c để S∆ABC nhỏ nhất
Câu 12: Tính giá trị của biểu thức:
A=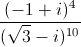 +
+ 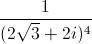 ; i2=-1
; i2=-1
Bạn có đủ giỏi để vượt qua
| Xếp hạng | Thành viên | Đúng | Làm | Đạt | Phút |
| 1 |
|
5 | 5 | 100% | 153.63 |
| 2 |
|
3 | 3 | 100% | 10.93 |
| 3 |
|
4 | 9 | 44% | 0.25 |
| 4 |
|
0 | 0 | 0% | 0.1 |
| 5 |
|
0 | 9 | 0% | 2.35 |