Cho (O) đường kính AB; trên tia đối của tia AB lấy điểm C, vẽ đường thẳng d vuông góc với AB tại C; lấy điểm M bất kỳ trên đường tròn, tia BM cắt d tại D, tia DA cắt (O) tại điểm thứ hai E.
a) Chứng minh tứ giác ACDM là tứ giác nội tiếp.
b) Chứng minh: BM.BD = BA.BC
c) Chứng minh MA là phân giác \(\angle CME\)
d) Giả sử CA = 4 cm; AB = 9 cm. Tìm vị trí của điểm M trên (O) để khoảng cách giữa hai điểm D và E nhỏ nhất.
Câu 539534: Cho (O) đường kính AB; trên tia đối của tia AB lấy điểm C, vẽ đường thẳng d vuông góc với AB tại C; lấy điểm M bất kỳ trên đường tròn, tia BM cắt d tại D, tia DA cắt (O) tại điểm thứ hai E.
a) Chứng minh tứ giác ACDM là tứ giác nội tiếp.
b) Chứng minh: BM.BD = BA.BC
c) Chứng minh MA là phân giác \(\angle CME\)
d) Giả sử CA = 4 cm; AB = 9 cm. Tìm vị trí của điểm M trên (O) để khoảng cách giữa hai điểm D và E nhỏ nhất.
-
Giải chi tiết:
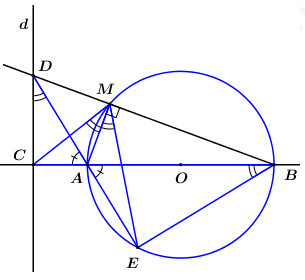
a) Chứng minh tứ giác ACDM là tứ giác nội tiếp. (1 điểm)
Xét \(\left( O \right)\): \(\angle AMB = {90^0}\) (góc nội tiếp chắn nửa đường tròn).
\( \Rightarrow \angle AMD = {90^0}\) (kề bù \(\angle AMB = {90^0}\))
Mà \(\angle ACD = {90^0}\,\,\left( {d \bot CB} \right)\)
\( \Rightarrow \angle AMD + \angle ACD = {180^0}\)
Xét tứ giác \(ACDM\): \(\angle AMD + \angle ACD = {180^0}\)
Mà \(\angle AMD,\,\,\angle ACD\) là 2 góc đối nhau
\( \Rightarrow \) Tứ giác \(ACDM\) là tứ giác nội tiếp (dhnb tgnt).
b) Chứng minh: BM.BD = BA.BC (1 điểm)
Xét \(\Delta BMA\) và \(\Delta BCD\)
\(\begin{array}{l}\angle CBD\,\,chung\\\angle BMA = \angle BCD = {90^0}\\ \Rightarrow \Delta BMA \sim \Delta BCD\,\,\left( {g.g} \right)\end{array}\)
\( \Rightarrow \dfrac{{BM}}{{BC}} = \dfrac{{BA}}{{BD}}\) (định nghĩa 2 tam giác đồng dạng)
\( \Rightarrow BM.BD = BA.BC\,\,\,\left( {dpcm} \right)\)
c) Chứng minh MA là phân giác \(\angle CME\) (1 điểm)
Xét \(\left( O \right)\): \(\angle AEB = {90^0}\) (góc nội tiếp chắn nửa đường tròn).
\( \Rightarrow \Delta AEB\) vuông tại \(E\)
\( \Rightarrow \angle ABE + \angle BAE = {90^0}\).
Mà \(\angle CDA + \angle CAD = {90^0}\) (do \(\Delta ACD\) vuông tại \(C\)).
\(\angle CAD = \angle BAE\) (2 góc đối đỉnh).
\( \Rightarrow \angle ABE = \angle CDA\,\,\left( 1 \right)\)
Xét \(\left( O \right)\): \(\angle ABE = \angle AME\) (2 góc nội tiếp cùng chắn cung \(AE\)) (2)
Xét đường tròn ngoại tiếp tứ giác \(ACDM\): \(\angle CDA = \angle CMA\) (2 góc nội tiếp cùng chắn cung \(AC\)) (3)
Từ (1), (2), (3) \( \Rightarrow \angle CMA = \angle EMA \Rightarrow MA\) là tua phân giác của \(\angle CME\) (đpcm).
d) Giả sử CA = 4 cm; AB = 9 cm. Tìm vị trí của điểm M trên (O) để khoảng cách giữa hai điểm D và E nhỏ nhất. (0.5 điểm)
\(DE = DA + AE\mathop \ge \limits^{Co - si} 2\sqrt {DA.AE} \)
Ta chứng minh được \(DA.AE = AC.AB = 4.9 = 36\).
\(\begin{array}{l} \Rightarrow DE \ge 2\sqrt {36} \Leftrightarrow DE \ge 12\\ \Rightarrow D{E_{\min }} = 12 \Leftrightarrow \left\{ \begin{array}{l}DA = AE\\DE = 12\end{array} \right. \Rightarrow DA = AE = 6\,\,cm\end{array}\)
\(DC = \sqrt {D{A^2} - A{C^2}} = \sqrt {{6^2} - {4^2}} = \sqrt {20} \).
\(\Delta CDB\) vuông tại \(C \Rightarrow \tan \angle CBD = \dfrac{{CD}}{{CB}} = \dfrac{{\sqrt {20} }}{{13}}\).
Vậy \(DE\) nhỏ nhất \( = 12 \Leftrightarrow M \in \left( O \right)\) sao cho \(\tan \angle CBD = \dfrac{{\sqrt {20} }}{{13}}\).
Lời giải sai Bình thường Khá hay Rất Hay
Tham Gia Group 2K9 Ôn Thi Vào Lớp 10 Miễn Phí
>> Học trực tuyến lớp 9 và luyện vào lớp 10 tại Tuyensinh247.com, cam kết giúp học sinh lớp 9 học tốt, hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
