Đề thi thử đại học môn Toán khối D lần 1 năm 2014 -Trường THPT Nguyễn Quang Diệu - Đồng Tháp

Thời gian thi : 180 phút - Số câu hỏi : 12 câu - Số lượt thi : 1091

Click vào đề thi  

Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"

Một số câu hỏi trong đề thi

Câu 1: Cho hàm số y=−x4 −2mx2 +m2 +m   (1) , với m là tham số thực.

a) Khảo sát sự biến thiên và vẽ đồ thị hàm số  (1) khi m=−2. 

b) Tìm tất cả các giá trị của m để đồ thị hàm số (1) cắt trục hoành tại bốn điểm phân biệt. 

Câu 2: Giải phương trình:  2sin x+cos3x+sin2x=1+sin4x. 

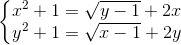
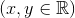
Câu 3: Giải hệ phương trình: \left\{\begin{matrix} x^{2}+1=\sqrt{y-1}+2x & \\ y^{2}+1=\sqrt{x-1}+2y& \end{matrix}\right. (x,y\in \mathbb{R})

Câu 4: Tính tích phân: I=\int_{-\frac{1}{2}}^{3}\frac{xdx}{\sqrt[3]{2x+2}}

Câu 5: Cho hình chóp S.ABCD có đáy hình chữ nhật, AB=a; AC=2a, SA vuông góc với mặt phẳng (ABCD), SC tạo với mặt phẳng (SAB) một góc 300. Gọi M là một điểm trên cạnh AB sao cho BM=3MA. Tính theo a thể tích của khối hình chóp S.DCM và khoảng cách từ A đến mặt phẳng (SCM).

 

Câu 6: Cho các số thực x,y thỏa mãn 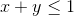x+y\leq 1. Tìm giá trị nhỏ nhất của biểu thức: 

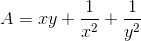
A=xy+\frac{1}{x^{2}}+\frac{1}{y^{2}}

Câu 7: Trong mặt phẳng với hệ trục tọa độ (Oxy), cho hình vuông ABCD có A (2;-4), đỉnh C thuộc đường thẳng d :3x + y + 2 = 0. Đường thẳng DM : x − y−2 = 0 , với M là trung điểm của AB. Xác định tọa độ các đỉnh B,C,D biết rằng đỉnh C có hoành độ âm.

 

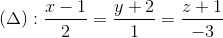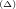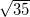Câu 8: Trong không gian với hệ tọa độ Oxyz , cho điểm A(2;-5;-6) và đường thẳng (\Delta ):\frac{x-1}{2}=\frac{y+2}{1}=\frac{z+1}{-3}.Tìm tọa độ hình chiếu vuông góc của A trên (\Delta ). Viết phương trình đường thẳng đi qua A và cắt (∆) tại B sao cho AB =\sqrt{35}. 

Câu 9: Từ các chữ số 0, 1, 2, 3, 4, 5 có thể lập được bao nhiêu số tự nhiên gồm bốn chữ số khác nhau, trong đó phải có chữ số 2 và 4 ?

Câu 10: Trong mặt phẳng với hệ trục tọa độ (Oxy), cho hình chữ nhật ABCD có diện tích bằng 48, đỉnh D(−3;2). Đường phân giác của góc 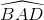\widehat{BAD} có phương trình ∆: x+y−7 = 0 . Tìm tọa độ đỉnh B biết   đỉnh A có hoành độ dương.

Câu 11: Trong không gian với hệ tọa độ Oxyz , cho điểm A(4;3;2) và đường thẳng 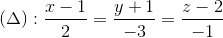  (\Delta ):\frac{x-1}{2}=\frac{y+1}{-3}=\frac{z-2}{-1}. Tính khoảng cách từ A đến (\Delta ). Viết phương trình đường thẳng đi qua A , cắt và  vuông góc với (∆).

Câu 12: Tìm giá trị lớn nhất và nhỏ nhất của hàm số:                                               

f(x)= x+ 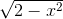\sqrt{2-x^{2}}

Bạn có đủ giỏi để vượt qua

cao.khanhvinh Cao Khánh Vinh
Xếp hạng Thành viên Đúng Làm Đạt Phút
1 Cao Khánh Vinh 9 9 100% 0.83
2 Phan Hương Mèo 7 7 100% 71.07
3 Nhã Uyên Trịnh Nguyễn 7 7 100% 100
4 phamthiTuyen 7 9 78% 18.68
5 Phi Phi 7 9 78% 30.35
6 Thao Uyen Nghiem Nguyen 4 4 100% 122.48
7 Pukan Mon 5 9 56% 0.4
8 Nu meo 3 3 100% 3.2
9 Tít Tử Tế 3 3 100% 8.12
10 Nguyễn Văn  3 3 100% 27.12
11 Phương Quỳnh 3 3 100% 59.95
12 Tran Ngoc Qui Apples 3 3 100% 66.62
13 Nguyễn Thanh Hương 3 4 75% 82.47
14 trần thương thương 2 2 100% 180.28
15 Nguyen Le Duy Bao 2 4 50% 72.85
16 phuonglinh 3 7 43% 0.9
17 laikimoanh 1 2 50% 87.87
18 vo kim thien 1 2 50% 0.37
19 Takkehoa QH 0 0 0% 2.22
20 Bông Hoa 2 6 33% 4.57
21 Phan Tom 0 0 0% 0.15
22 Nguyễn Tất Tường 0 0 0% 0.5
23 dang thi xuan nhan 0 0 0% 0.95
24 Nguyên Ngố 3 9 33% 2.9
25 duc 0 0 0% 0.35
26 thanglq 0 0 0% 0.07
27 lam hoang viet 0 0 0% 0.65
28 Huỳnh Anh 7 12 58% 16.4
29 Tuyet Yeu Thuong 0 0 0% 35.88
30 nguyễn văn dũng 0 0 0% 0.25
31 jenny 0 0 0% 0.27
32 trinh gia huy 0 0 0% 0.25
33 Mềnhrấtlàvui Nólạidàingoằn Nghèođếnnhưvầy 0 0 0% 0.3
34 Hồng Quắt 4 11 36% 2.68
35 nuyen thi cam duyen 0 0 0% 0.2
36 Chinh Pham 0 0 0% 0.17
37 Tớ Là Nhân Mã 0 0 0% 0.2
38 Tạ Thùy Dương 4 12 33% 2.08
39 ngtrungthanh 0 0 0% 0.1
40 Trần Gia Bảo 0 0 0% 44.57
41 Xuân Hinh 0 0 0% 0.2
42 Trần Tuấn Anh 0 0 0% 0.17
43 nguyen thi thuy 0 0 0% 0.15
44 NGUYỄN DOÃN LÂM 0 0 0% 3.52
45 Phương Tuấn 0 0 0% 0.23
46 Sẽcóngười Cầnanh 0 0 0% 0.23
47 Nhã Nguyễn 0 0 0% 73.25
48 Thỏ Ngọc 0 0 0% 0.63
49 Bùi Hiếu 0 0 0% 0.05
50 Tran Huu Vy 1 3 33% 17.18
51 Đt Huỳnh 0 0 0% 0.12
52 Linh Nhỏ 0 0 0% 0.37
53 ngen thi van anh 0 0 0% 0.07
54 Đồng Văn Hưng 0 0 0% 0.15
55 nguyễn chang 0 0 0% 21.17
56 Mai Thanh Dat 0 0 0% 0.47
57 Mưa Hạ 0 0 0% 0.05
58 Dinh Duc 0 0 0% 0.42
59 I̵̡̢̛̻̜̙̫͇̮͚̠̜̞̥̜̥̘̣̳̖͎̮͈̦̱̅̈͗́̃̂̋̿̔̄͌̈́͗̒̔̒̀͛̊͐̈́͊̕͝Ģ̶̟͖̺̘͖̝̩ͅi̶̬̤̤͓͎̯̣̭̠͜ó̷̺̮̠͖͓̫͓̗͜ ̷̜̩̥̟̟͜V̴̤̺̳͚ͅô̶̡̢͈̯̭͎͍̜̗̫͍̭͚̻ Ţ̴̡̻̳̝͎̯̬͈̠͓͇̹̖͓͇̭͔ị̶̢̢̧̧̞̙͕̠̮̥̣̺̀n̴̨̪̥̺̠͔̤̞̼͕̹̞͙̪̩̬h̵̡̙͕̼̹̜͚̫͇͇̝̞̥̦ì̸̡̖̟̙͕͚͕͍͚̟̗̪͕̗̮̞̏̿̏̚ 0 0 0% 0.12
60 Nhi Yến 0 1 0% 0.2
61 truong ngoc hien 2 9 22% 1.97
62 Nguyễn Tuệ Linh 0 3 0% 3.05
63 vhbk 1 9 11% 1.77
64 Nguyễn thị huyền trang 1 9 11% 10.03
65 Lieu Bui 1 9 11% 0.9
66 Lananh Hoang 1 9 11% 12.23

Cùng tham gia trao đổi với bạn bè!

Lớp 12