Đề thi Cao đẳng môn Toán khối A, A1, B, D năm 2013
Thời gian thi : 180 phút - Số câu hỏi : 12 câu - Số lượt thi : 538
Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"
Một số câu hỏi trong đề thi
Câu 1: Cho hàm số y = 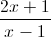 . a)Khảo sát sự biến thiên và vẽ đồ thị (C ) của hàm số đã cho. b)Gọi M là điểm thuộc (C) có tung độ bằng 5. Tiếp tuyến của (C ) tại M cắt các trục tọa độ Ox và Oy lần lượt tại A và B. Tính diện tích tam giác OAB.
. a)Khảo sát sự biến thiên và vẽ đồ thị (C ) của hàm số đã cho. b)Gọi M là điểm thuộc (C) có tung độ bằng 5. Tiếp tuyến của (C ) tại M cắt các trục tọa độ Ox và Oy lần lượt tại A và B. Tính diện tích tam giác OAB.
Câu 2: Giải phương trình cos(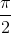 - x) + sin2x = 0.
- x) + sin2x = 0.
Câu 3: Giải hệ phương trình 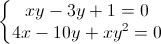 (x, y ∈R).
(x, y ∈R).
Câu 4: Tính tích phân I = 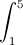
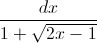 .
.
Câu 5: Cho lăng trụ đều ABC.A’B’C’ có AB = a và đường thẳng A’B tạo với đáy một góc bằng 600. Gọi M và N lần lượt là trung điểm của các cạnh AC và B’C’. Tính theo a thể tích của khối lăng trụ ABC.A’B’C’ và độ dài đoạn MN.
Câu 6: Tìm m để bất phương trình (x – 2 – m)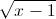 ≤ m – 4 có nghiệm.
≤ m – 4 có nghiệm.
Câu 7: Trong mặt phẳng với hệ tọa độ Oxy, cho các đường thẳng d: x + y – 3 = 0, ∆ : x – y + 2 = 0 và điểm M(-1; 3). Viết phương trình đường tròn đi qua M, có tâm thuộc d, cắt ∆ tại hai điểm A và B sao cho AB = 3√2.
Câu 8: Trong không gian với hệ tọa độ Oxyz, cho điểm A(4; -1;3) và đường thẳng d: 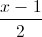 =
= 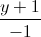 =
= 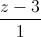 . Tìm tọa độ điểm đối xứng của A qua d.
. Tìm tọa độ điểm đối xứng của A qua d.
Câu 9: Cho số phức z thỏa mãn điều kiện (3 + 2i)z + (2 – i)2 = 4 + i. Tìm phần thực và phần ảo của số phức w = (1 + z)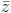 .
.
Câu 10: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC vuông tại A(-3;2) và có trọng tâm là G( ;
;  ). Đường cao kẻ từ đỉnh A của tam giác ABC đi qua điểm P(-2;0). Tìm tọa độ các điểm B và C.
). Đường cao kẻ từ đỉnh A của tam giác ABC đi qua điểm P(-2;0). Tìm tọa độ các điểm B và C.
Câu 11: Trong không gian với hệ tọa độ Oxyz, cho điểm A(-1; 3;2) và mặt phẳng (P) : 2x – 5y + 4z – 36 = 0. Gọi I là hình chiếu vuông góc của A trên mặt phẳng (P). Viết phương trình mặt cầu tâm I và đi qua điểm A.
Câu 12: Giải phương trình z2 + (2 – 3i)z – 1 – 3i = 0 trên tập hợp C các số phức.
Bạn có đủ giỏi để vượt qua
| Xếp hạng | Thành viên | Đúng | Làm | Đạt | Phút |
| 1 |
|
8 | 8 | 100% | 29.68 |
| 2 |
|
8 | 9 | 89% | 74.43 |
| 3 |
|
7 | 8 | 88% | 91.45 |
| 4 |
|
7 | 9 | 78% | 103.95 |
| 5 |
|
6 | 6 | 100% | 34.23 |
| 6 |
|
7 | 9 | 78% | 4.13 |
| 7 |
|
6 | 6 | 100% | 84.67 |
| 8 |
|
5 | 6 | 83% | 23.5 |
| 9 |
|
5 | 9 | 56% | 95.12 |
| 10 |
|
3 | 3 | 100% | 18.68 |
| 11 |
|
5 | 9 | 56% | 36.15 |
| 12 |
|
3 | 4 | 75% | 27.13 |
| 13 |
|
2 | 2 | 100% | 49.6 |
| 14 |
|
2 | 2 | 100% | 26.55 |
| 15 |
|
3 | 6 | 50% | 1.23 |
| 16 |
|
1 | 1 | 100% | 5.28 |
| 17 |
|
7 | 12 | 58% | 7.97 |
| 18 |
|
3 | 9 | 33% | 0.78 |
| 19 |
|
3 | 9 | 33% | 0.65 |
| 20 |
|
3 | 9 | 33% | 5.87 |
| 21 |
|
5 | 6 | 83% | 19.3 |
| 22 |
|
3 | 9 | 33% | 0.37 |
| 23 |
|
0 | 0 | 0% | 0.53 |
| 24 |
|
0 | 0 | 0% | 0.47 |
| 25 |
|
9 | 12 | 75% | 16.98 |
| 26 |
|
2 | 8 | 25% | 4.05 |
| 27 |
|
1 | 6 | 17% | 0.9 |
| 28 |
|
2 | 9 | 22% | 0.35 |
| 29 |
|
2 | 9 | 22% | 0.52 |