Anh Minh vừa mới xây một cái hồ trữ nước cạnh nhà có hình dạng hộp chữ nhật kích thước
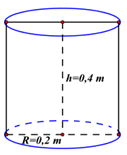
Anh Minh vừa mới xây một cái hồ trữ nước cạnh nhà có hình dạng hộp chữ nhật kích thước \(2m \times 2m \times 1m.\) Hiện hồ chưa có nước nên anh Minh phải ra sông lấy nước. Mỗi lần ra sông anh gánh được 1 đôi nước gồm 2 thùng hình trụ bằng nhau có bán kính đáy \(0,2\,\,m,\) chiều cao \(0,4\,m.\)
Trả lời cho các câu 1, 2 dưới đây:
Tính lượng nước \(\left( {{m^3}} \right)\) anh Minh đổ vào hồ sau mỗi lần gánh (ghi kết quả làm tròn đến 2 chữ số thập phân). Biết trong quá trình gánh nước về thì lượng nước bị hao hụt khoảng \(10\% \) và công thức tính thể tích hình trụ là \(V = \pi {R^2}h.\)
Đáp án đúng là: B
Tính thể tích \({V_1}\) của 2 thùng nước mỗi lần anh Minh gánh được.
Thể tích thực tế anh Minh gánh được là: \(V = 90\% {V_1}.\)
Đáp án cần chọn là: B
Hỏi anh Minh phải gánh ít nhất bao nhiêu lần để đầy hồ? Bỏ qua thể tính thành hồ.
Đáp án đúng là: A
Tính thể tích \({V_0} = abc\) của hồ nước.
Số lần ít nhất anh Minh cần gánh nước là: \(n = \left[ {\frac{{{V_0}}}{V}} \right].\)
Đáp án cần chọn là: A
Quảng cáo
PH/HS 2K10 THAM GIA NHÓM ĐỂ CẬP NHẬT ĐIỂM THI, ĐIỂM CHUẨN MIỄN PHÍ!
>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
