Đánh giá năng lực Hà Nội
Đánh giá năng lực Hà Nội
Tìm số tự nhiên \(a\) biết rằng khi cộng cả tử và mẫu của phân số \(\dfrac{37}{53}\) cho \(a\)
Tìm số tự nhiên \(a\) biết rằng khi cộng cả tử và mẫu của phân số \(\dfrac{37}{53}\) cho \(a\) ta được phân số mới bằng \(\dfrac34\)
Đáp án đúng là: A
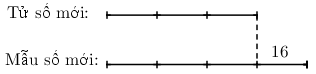
Khi cộng cả tử và mẫu của phân số với cùng một số tự nhiên thì hiệu của tử số và mẫu số không đổi, nên ta lập được sơ đồ hiệu tỉ giữa tử số và mẫu số mới. Từ đó tìm được tử số mới. Lấy tử số (mẫu số) mới trừ đi tử số (mẫu số) cũ ta được số tự nhiên \(a\) cần tìm.
Hiệu giữa tử số và mẫu số của phân số \(\dfrac{37}{53}\) là:
\(53-37=16\)
Khi cộng cả tử và mẫu của phân số với cùng một số tự nhiên thì hiệu của tử số và mẫu số không đổi và bằng \(16\)
Ta có sơ đồ:
Hiệu số phần bằng nhau là:
\(4-3=1\) (phần)
Tử số mới là:
\(16\times 3=48\)
Số phải tìm là:
\(48-37=11\)
Đáp số: \(a=11\)
Tham Gia Group Dành Cho 2K14 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến các môn Toán, Tiếng Việt, Tiếng Anh lớp 5 trên Tuyensinh247.com cam kết giúp con lớp 5 học tốt, hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
