Cho hai mạch dao động kín lí tưởng L1C1 và L2C2 đang có dao động điện điều hòa. Gọi d1,d2

Câu hỏi số 308675:

Vận dụng cao

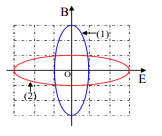
Cho hai mạch dao động kín lí tưởng L₁C₁ và L₂C₂ đang có dao động điện điều hòa. Gọi d₁,d₂ là khoảng cách hai bản tụ khi đó C₁ = m/d₁ và C₂ = m/d₂ (m là hằng số). Hai cuộn dây trong hai mạch giống nhau, gọi E là cường độ điện trường trong khoảng giữa hai bản tụ, B là cảm ứng từ trong cuộn dây. Xét đường biểu diễn mối quan hệ E và B trong mạch LC có dạng như hình. (đường 1 mạch L₁C₁, đường 2 mạch L₂C₂). Tỉ số d₂/d₁ gần bằng giá trị nào sau đây

A. 27

B. 81

C. 1/27

D. 1/8

Đáp án đúng là: D

Quảng cáo

Xem lời giải

Câu hỏi:308675

Phương pháp giải

Cường độ điện trường E = U/d

Từ trường trong lòng ống dây B = kI

Năng lượng diện trường cực đại bằng năng lượng từ trường cực đại nên CU₀² = LI₀²

Giải chi tiết

Do \(CU_{0}^{2}=LI_{0}^{2}\Rightarrow \frac{{{U}_{0}}}{{{I}_{0}}}=\sqrt{\frac{L}{C}}=\sqrt{\frac{Ld}{m}}\)

+ Trường hợp mach L₁C₁ thì B_max = 3E_maxnên

\(kI_{0}^{{}}=3\frac{{{U}_{0}}}{{{d}_{1}}}\Rightarrow \frac{{{U}_{0}}}{{{I}_{0}}}=\frac{k{{d}_{1}}}{3}\Rightarrow \sqrt{\frac{{{L}_{1}}{{d}_{1}}}{m}}=\frac{k{{d}_{1}}}{3}\Rightarrow \frac{{{L}_{1}}{{d}_{1}}}{m}=\frac{{{k}^{2}}d_{1}^{2}}{9}\Rightarrow {{d}_{1}}=\frac{9{{L}_{1}}}{m{{k}^{2}}}\)

+ Trường hợp mạch L₂C₂ thì E_max = 3B_maxnên:

\(3kI_{0}^{{}}=\frac{{{U}_{0}}}{{{d}_{2}}}\Rightarrow \frac{{{U}_{0}}}{{{I}_{0}}}=3k{{d}_{2}}\Rightarrow \sqrt{\frac{{{L}_{2}}{{d}_{2}}}{m}}=3k{{d}_{2}}\Rightarrow \frac{{{L}_{2}}{{d}_{2}}}{m}=9{{k}^{2}}d_{2}^{2}\Rightarrow {{d}_{2}}=\frac{{{L}_{2}}}{9m{{k}^{2}}}\)

+ Mà B_1max = 3B_2max nên kI_1max = 3kI_2max \(\Rightarrow \frac{{{L}_{1}}}{{{L}_{2}}}=\frac{I_{2\max }^{2}}{I_{1\max }^{2}}=\frac{1}{9}\)

Vậy \(\frac{{{d}_{2}}}{{{d}_{1}}}=\frac{1}{81}.\frac{{{L}_{2}}}{{{L}_{1}}}=\frac{1}{9}\)

Đáp án cần chọn là: D

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.