Trong mặt phẳng tọa độ \(Oxy\), cho \(A\left( {1;2} \right);\,\,B\left( {4;4} \right)\). Tìm điểm \(M\)

Câu hỏi số 354028:

Vận dụng

Trong mặt phẳng tọa độ \(Oxy\), cho \(A\left( {1;2} \right);\,\,B\left( {4;4} \right)\). Tìm điểm \(M\) thuộc \(Ox\) sao cho \(MA + MB\) nhỏ nhất?

A. \(M\left( {1;0} \right)\)

B. \(M\left( {4;0} \right)\)

C. \(M\left( {2;0} \right)\)

D. \(\left( {\frac{5}{2};0} \right)\)

Đáp án đúng là: C

Quảng cáo

Xem lời giải

Câu hỏi:354028

Phương pháp giải

Bài toán: Trong mặt phẳng cho hai điểm phân biệt \(A,\,B\) và không nằm trên đường thẳng \(\Delta \) cho trước. Tìm điểm \(M \in \Delta \) sao cho \(MA + MB\) nhỏ nhất.

+ TH1: A và B nằm khác phía đối với \(\Delta \). Khi đó ta có \(MA + MB \ge AB\), dấu bằng xảy ra khi \(M,\,\,A,\,\,B\) thẳng hàng, tức \(M = AB \cap \Delta \)

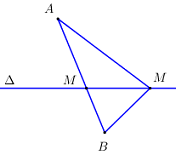
+ TH2: A và B nằm cùng phía đối với \(\Delta \). Ta gọi \(A'\) là ảnh của \(A\) qua Đ\(_\Delta \). Khi đó \(\forall M \in \Delta :\,\,MA + MB = MA' + MB\).

Mà \(MA' + MB\) bé nhất khi \(M,\,\,A',\,\,B\) thẳng hàng hay \(M = A'B \cap \Delta \).

Giải chi tiết

+ Dễ thấy \(A,B\) nằm cùng phía so với trục \(Ox\).

+ Gọi \(A' = \) Đ\(_{Ox}\left( A \right) \Rightarrow A'\left( {1; - 2} \right)\); khi đó ta có \(MA = MA'\).

\( \Rightarrow MA + MB = MA' + MB \ge A'B\).

Dấu "=" xảy ra \( \Leftrightarrow M,\,\,A',\,\,B\) thẳng hàng hay \(M = A'B \cap Ox\).

+ Phương trình \(A'B:\,\,\frac{{x - 1}}{{4 - 1}} = \frac{{y + 2}}{{4 + 2}} \Leftrightarrow 2\left( {x - 1} \right) = y + 2 \Leftrightarrow 2x - y - 4 = 0\).

+ Tọa độ của \(M\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}2x - y - 4 = 0\\y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 0\end{array} \right. \Rightarrow M\left( {2;0} \right)\).

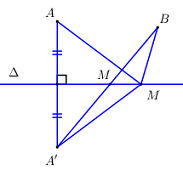
Đáp án cần chọn là: C

Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.