a) Một tấm thủy tinh có hai mặt song song và cách nhau 20cm, chiết suất n = 1,5 được đặt trong
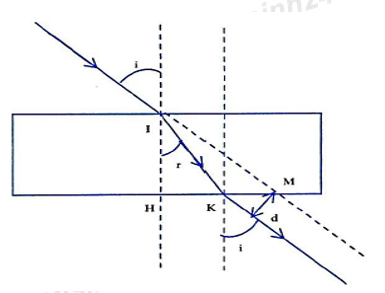
a) Một tấm thủy tinh có hai mặt song song và cách nhau 20cm, chiết suất n = 1,5 được đặt trong không khí. Chiếu tới tấm đó một tia sáng SI có góc tới 450. Tính khoảng cách d giữa giá của tia tới và tia ló.
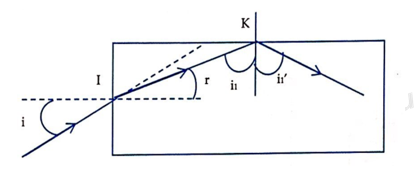
b) Một sợi cáp quang hình trụ có lõi và vỏ được làm bằng các chất trong suốt. Biết mọi tia sáng đi xiên góc vào tiết diện thẳng của một đầu dây đều bị phản xạ toàn phần ở thành và chỉ ló ra ở đầu dây còn lại. Tìm điều kiện về chiết suất tỉ đối của lõi so với vỏ sợi cáp quang này.
Đáp án đúng là: B
Quảng cáo
a) Vẽ hình
Áp dụng công thức định luật khúc xạ ánh sáng:
\(\frac{{\sin i}}{{\sin r}} = \frac{{{n_2}}}{{{n_1}}}\)
và các công thức lượng giác trong tam giác
b) Vẽ hình
Áp dụng công thức định luật khúc xạ ánh sáng: \(\frac{{\sin i}}{{\sin r}} = \frac{{{n_2}}}{{{n_1}}}\)
Công thức tính góc giới hạn phản xạ toàn phần:
\(\sin {i_{gh}} = \frac{{{n_2}}}{{{n_1}}}\)
Áp dụng các công thức lượng giác trong tam giác.
Tóm tắt:
a) Bản mặt song song có e = 20 cm; n = 1,5; góc tới i = 450; Tính d giữa tia tới và tia ló?
b) Sợi cáp quang: Tìm điều kiện về chiết suất tỉ đối của lõi so với vỏ sợi cáp quang này để mọi tia tới đều bị phản xạ tại mặt phân cách giữa lõi và vỏ, để tia sáng ló ra đầu kia.
Bài làm:
a) Ta có hình vẽ:
Áp dụng công thức khúc xạ tại I:
\(\frac{{\sin i}}{{\sin r}} = \frac{{{n_2}}}{{{n_1}}} \Leftrightarrow \frac{{\sin 45}}{{\sin r}} = \frac{{{n_2}}}{{{n_1}}} = \frac{{1,5}}{1} \Rightarrow r = 28,{126^0}\)
Ta có:
\(KM = HM - HK = IH\left( {\tan i - \tan r} \right)\)
\(\begin{array}{l}
KM = 20.\left( {\tan {{45}^0} - \tan 28,{{126}^0}} \right) = 9,31\left( {cm} \right)\\
d = KM.\sin \left( {{{90}^0} - {{45}^0}} \right) = 6,58\left( {cm} \right)
\end{array}\)
b) Ta có hình vẽ:
Xét khúc xạ tại I:
\(\sin i = n.\sin r{\rm{ }}\left( 1 \right)\)
Xét phản xạ toàn phần tại K:
\(\sin {i_1} \ge \frac{1}{n}\,\,\,\left( 2 \right)\)
Theo hình:
\({i_1} + r = {90^0}\,\,\,\left( 3 \right)\)
Từ (3) \( \Rightarrow \sin {i_1} = \cos r = \sqrt {1 - {{\sin }^2}r} \,\,\,\,\left( 4 \right)\)
Kết hợp (1); (2); (4) ta có:
\(\sqrt {1 - \frac{{{{\sin }^2}i}}{{{n^2}}}} \ge \frac{1}{n} \Rightarrow {n^2} \ge 1 + {\sin ^2}i \Rightarrow n \ge \sqrt {1 + {{\sin }^2}i} \)
Thỏa mãn với mọi giá trị của góc tới i vậy
\(n \ge \sqrt 2 = 1,4142\)
Đáp án cần chọn là: B
Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
