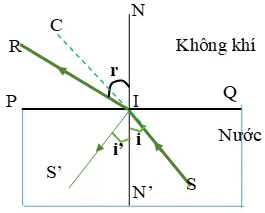
Chiếu một chùm tia sáng hẹp song song, đơn sắc từ môi trường trong suốt có chiết suất \(n\) ra
Chiếu một chùm tia sáng hẹp song song, đơn sắc từ môi trường trong suốt có chiết suất \(n\) ra không khí, dưới góc tới \({30^0}\) thì tia khúc xạ lệch so với phương tia tới một góc \({15^0}\).
Vẽ đường truyền của tia sáng. Tính chiết suất \(n\) của môi trường.
Để không có tia khúc xạ ra không khí thì góc tới phải tăng thêm ít nhất bao nhiêu độ?
Đáp án đúng là: A
Quảng cáo
+ Biểu thức của định luật khúc xạ ánh sáng: \({n_1}.\sin i = {n_2}.\sin \,r\)
+ Điều kiện xảy ra hiện tượng phản xạ toàn phần: \(\left\{ {\begin{array}{*{20}{l}}
{{n_1} > {n_2}}\\
{i \ge {i_{gh}};\,\,\,\sin {i_{gh}} = \frac{{{n_2}}}{{{n_1}}}}
\end{array}} \right.\)
+ Đường truyền của tia sáng:
Vì góc khúc xạ lệch so với góc tới \({15^0}\) nên ta có góc khúc xạ bằng:
\(r = i + {15^0} = 30 + 15 = {45^0}\)
Áp dụng định luật khúc xạ ánh sáng ta có:
\(\frac{{\sin i}}{{\sin r}} = \frac{{{n_2}}}{{{n_1}}} \Leftrightarrow \frac{{\sin {{30}^0}}}{{\sin {{45}^0}}} = \frac{1}{n} \Rightarrow n = \frac{{\sin {{45}^0}}}{{\sin {{30}^0}}} = \sqrt 2 {\rm{ }}\)
+ Vì ánh sáng đi từ môi trường chiết quang hơn sang môi trường kém chiết quang hơn nên có thể xảy ra hiện tượng phản xạ toàn phần khi: \(i \ge {i_{gh}}\)
Góc tới giới hạn được xác định bởi:
\(\sin {i_{gh}} = \frac{{{n_2}}}{{{n_1}}} = \frac{1}{{\sqrt 2 }} \Rightarrow {i_{gh}} = {45^0}\)
Vậy góc tới \(i \ge {i_{gh}} \Leftrightarrow i \ge {45^0}\) thì không còn tia khúc xạ.
Vậy góc tới nhỏ nhất là \({45^0}\) để không còn tia khúc xạ.
Khi đó, ta cần tăng góc tới thêm:
\(\Delta i = {45^0}-{30^0} = {15^0}\)
Đáp án cần chọn là: A
Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
