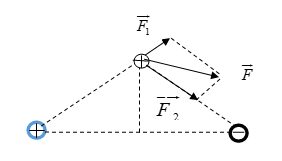
Hai điện tích điểm \({q_1} = {10^{ - 8}}C\) và \({q_2} = - {3.10^{ - 8}}C\) đặt trong không khí tại hai
Hai điện tích điểm \({q_1} = {10^{ - 8}}C\) và \({q_2} = - {3.10^{ - 8}}C\) đặt trong không khí tại hai điểm A và B cách nhau 8 cm. Đặt điện tích điểm \(q = {10^{ - 8}}C\) tại điểm M trên đường trung trực của đoạn thẳng AB và cách AB một khoảng 3 cm. Lấy \(k = {9.10^9}N{m^2}/{C^2}\) . Lực điện tổng hợp do \({q_1}\) và \({q_2}\) tác dụng lên q có độ lớn là
Đáp án đúng là: B
Quảng cáo
Áp dụng công thức Cu lông tính lực điện \(F = k.\frac{{|{q_1}.{q_2}|}}{{{r^2}}}\)
Vẽ hình. Sau đó ta tổng hợp vec to lực F tác dụng lên hạt điện tích điểm q theo quy tắc hình bình hành và tính lực tổng hợp.
Tóm tắt:
\({q_1} = {10^{ - 8}}C;{q_2} = - {3.10^{ - 8}}C;d = 8cm;k = {9.10^9}N{m^2}/{C^2}\)
Đặt \(q = {10^{ - 8}}C\) tại điểm M trên đường trung trực của đoạn thẳng AB và cách AB một khoảng 3cm.
F = ?
Giải:
Ta có hình vẽ:
Ta có :
\(\left\{ \begin{array}{l}
{F_1} = k.\frac{{\left| {{q_1}.q} \right|}}{{{r^2}}} = {9.10^9}.\frac{{\left| {{{10}^{ - 8}}{{.10}^{ - 8}}} \right|}}{{0,{{05}^2}}} = 3,{6.10^{ - 4}}N\\
{F_2} = k.\frac{{\left| {{q_2}.q} \right|}}{{{r^2}}} = {9.10^9}.\frac{{\left| { - {{3.10}^{ - 8}}{{.10}^{ - 8}}} \right|}}{{0,{{05}^2}}} = 10,{8.10^{ - 4}}N
\end{array} \right.\)
Góc tạo bởi hai vecto lực là
\(\alpha = {180^0} - 2.\left( {\arctan \frac{4}{3}} \right) = {73^0}44'\)
Độ lớn của lực tổng hợp là:
\(F = \sqrt {F_1^2 + F_2^2 + 2.{F_1}.{F_2}.\cos \alpha } = 12,{3.10^{ - 4}}N = 1,{23.10^{ - 3}}N\)
Đáp án cần chọn là: B
Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
