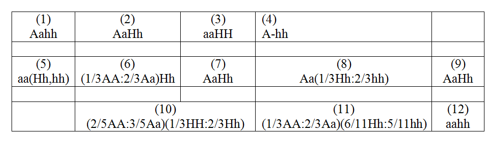
Cho sơ đồ phả hệ sau: Biết rằng hai cặp gen qui định hai tính trạng nói trên không cùng nằm

Câu hỏi số 416189:

Vận dụng cao

Cho sơ đồ phả hệ sau:

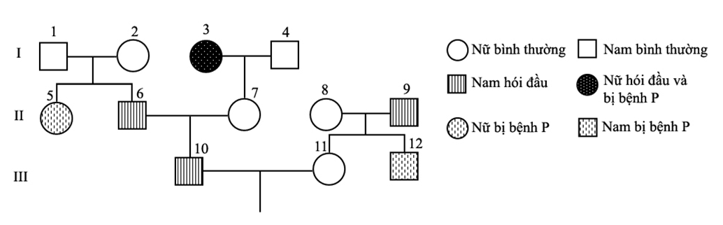
Biết rằng hai cặp gen qui định hai tính trạng nói trên không cùng nằm trong một nhóm gen liên kết: bệnh hói đầu do alen trội H nằm trên NST thường qui định, kiểu gen dị hợp Hh biểu hiện hói đầu ở người nam và không hói đầu ở người nữ và quần thể này ở trạng thái cân bằng và có tỉ lệ người bị hói đầu là 20%.

I. Có tối đa 5 người có kiểu gen đồng hợp về tính trạng hói đầu.

II. Xác định được chính xác kiểu gen của 7 người về cả hai tính trạng trên.

III. Khả năng người số 10 mang ít nhất 1 alen lặn là 13/15.

IV. Xác suất để đứa con đầu lòng của cặp vợ chồng số 10 và 11 là con gái, không hói đầu và không mang alen gây bệnh P là 2/11.

Theo lí thuyết, có bao nhiêu phát biểu đúng trong các phát biểu trên?

A. 1

B. 3

C. 4

D. 2

Đáp án đúng là: A

Quảng cáo

Xem lời giải

Câu hỏi:416189

Giải chi tiết

- Bệnh hói đầu:

+ Ở nam: HH + Hh: hói; hh: không hói.

+ Ở nữ: HH: hói; Hh + hh: không hói.

+ p2HH + 2pqHh + q2hh = 1.

$\left\{ {\begin{array}{*{20}{l}}{{p^2} + pq = 0,2}\\{p + q = 1}\end{array}} \right.$ → p = 0,2; q = 0,8.

+ CBDT: 0,04HH + 0,32Hh + 0,64hh = 1.

- Bố (1) và mẹ (2) không mắc bệnh P để con gái (5) mắc bệnh P → bệnh P do gen lặn nằm trên NST thường quy định.

(I) sai: Có tối đa 8 người có kiểu gen đồng hợp về tính trạng hói đầu: 1,3, 4, 5, 8,10,11,12.

Chú ý: Người số 2 bắt buộc phải Hh thì mới sinh được người con thứ (6) Hh.

(II) Sai: Chỉ có 6 người biết chính xác kiểu gen về cả 2 bệnh: 1,2,3,7, 9,12.

(III) Đúng: Người số 10 mang ít nhất 1 alen lặn = 1 – AAHH = $1 - \dfrac{2}{5} \times \dfrac{1}{3} = \dfrac{{13}}{{15}}$

(IV) sai: (10): $\left( {\dfrac{2}{5}AA:\dfrac{3}{5}Aa} \right)\left( {\dfrac{1}{3}HH:\dfrac{2}{3}Hh} \right) \times \left( {\dfrac{1}{3}AA:\dfrac{2}{3}Aa} \right)\left( {\dfrac{6}{{11}}Hh:\dfrac{5}{{11}}hh} \right)$

Giao tử: $\left( {\dfrac{7}{{10}}A:\dfrac{3}{{10}}a} \right)\left( {\dfrac{2}{3}H:\dfrac{1}{3}h} \right) \times \left( {\dfrac{2}{3}A:\dfrac{1}{3}a} \right)\left( {\dfrac{3}{{11}}H:\dfrac{8}{{11}}h} \right)$

→ con gái: $\dfrac{1}{2}AA\left( {Hh + hh} \right) = \dfrac{1}{2} \times \dfrac{7}{{10}} \times \dfrac{2}{3} \times \left( {1 - \dfrac{2}{3} \times \dfrac{3}{{11}}} \right) = \dfrac{{21}}{{110}}$

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.