Dùng mạch điện như hình bên để tạo ra dao động điện từ. Ban đầu đóng khóa K vào chốt a,

Câu hỏi số 500436:

Vận dụng

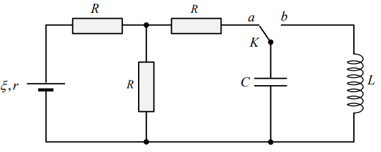
Dùng mạch điện như hình bên để tạo ra dao động điện từ. Ban đầu đóng khóa K vào chốt a, khi dòng điện chạy qua nguồn điện ổn định thì chuyển khóa K sang chốt b. Biết \(\xi = 5\,\,V;\,\,r = 1\,\,\Omega;\,\,R = 2\,\,\Omega ;\,\,L = \frac{9}{{10\pi }}\,\,mH\) và \(C = \frac{1}{\pi }\,\,\mu F\). Lấy \(e = 1,{6.10^{ - 19}}\,\,C\). Trong khoảng thời gian \(10\,\,\mu s\) kể từ thời điểm đóng K vào chốt b, có bao nhiêu êlectron đã chuyển đến bản tụ điện nối với khóa K?

A. \(4,{48.10^{12}}\,\,electron\).

B. \(4,{97.10^{12}}\,\,electron\).

C. \(1,{99.10^{12}}\,\,electron\).

D. \(1,{79.10^{12}}\,\,electron\).

Đáp án đúng là: C

Quảng cáo

Xem lời giải

Câu hỏi:500436

Phương pháp giải

Công thức định luật ôm: \(I = \frac{E}{{R + r}}\)

Điện tích tụ điện tích điện là: \(Q = CU\)

Khi khoá K ở b, mạch LC dao động với chu kì \(T = 2\pi \sqrt {LC} \)

Biểu diễn thời gian theo chu kì từ đó tính được điện tích đã chuyển đi: \(\Delta Q\).

Giải chi tiết

+ Khi khoá K ở a, cường độ dòng điện trong mạch là:

\(I = \frac{E}{{2R + r}} = \frac{5}{{2.2 + 1}} = 1\left( A \right)\)

Hiệu điện thế: \({U_{CI}} = {U_R} = I.R = 1.2 = 2\left( V \right)\)

Điện tích mà tụ điện tích được là:

\({Q_1} = C.{U_{CI}} = \frac{1}{\pi }{.10^{ - 6}}.2 = \frac{2}{\pi }{.10^{ - 6}}\left( C \right)\)

+ Khi khoá K ở vị trí b, mạch LC dao động với chu kì:

\(T = 2\pi \sqrt {LC} = 2\pi \sqrt {\frac{9}{{10\pi }}{{.10}^{ - 3}}.\frac{1}{\pi }{{.10}^{ - 6}}} = {6.10^{ - 5}}\left( s \right)\)

Mà \(\Delta t = 10\mu s = \frac{T}{6}\)

+ Tại thời điểm đóng K sang b thì điện tích trên tụ cực đại và bằng \({Q_1}\)

+ Sau \(\frac{T}{6}\) thì \({q_2} = \frac{{{Q_0}}}{{\sqrt 2 }} = \frac{{{Q_1}}}{{\sqrt 2 }}\) , lượng điện tích đã chuyển đi là:

\(\Delta Q = \frac{{{Q_0}}}{2} = \frac{1}{\pi }{.10^{ - 6}}\left( C \right) \approx 3,{18.10^{ - 7}}\left( C \right)\)

+ Số electron đã chuyển là:

\(n = \frac{{\Delta Q}}{{\left| e \right|}} = \frac{{3,{{18.10}^{ - 7}}}}{{1,{{6.10}^{ - 19}}}} = 1,{989.10^{12}} \approx 1,{99.10^{12}}\,\,\left( {electron} \right)\)

Đáp án cần chọn là: C

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.