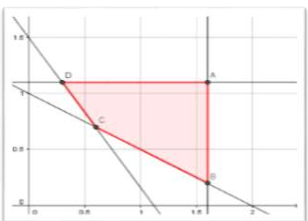
Một gia đình cần 900g chất prôtein và 400g chất lipit trong thức ăn mỗi ngày. Biết rằng thịt
Một gia đình cần 900g chất prôtein và 400g chất lipit trong thức ăn mỗi ngày. Biết rằng thịt bò chứa 80% prôtein và 20% lipit. Thịt lợn chứa 60% prôtein và 40% lipit. Biết rằng gia đình này chỉ mua nhiều nhất là 1600g thịt bò và 1100g thịt lợn, giá tiền 1kg thịt bò là 45 nghìn đồng, 1kg thịt lợn là 35 nghìn đồng. Hỏi gia đình đó phải mua bao nhiêu kg thịt mỗi loại để chi phí ít nhất?
Đáp án đúng là: B
Quảng cáo
Giả sử gia đình đó mua \(x(kg)\)thịt bò và \(y(kg)\) thịt lợn \((x,y \ge 0)\). Khi đó chi phí mua \(x(kg)\)thịt bò và \(y(kg)\)thịt lợn là \(T = 45x + 35y\) (nghìn đồng)
Theo giả thuyết, \(x\)và \(y\) thỏa mãn điều kiện \(x \le 1,6\); \(y \le 1,1\)
Khi đó lượng protein có được là \(80\% x + 60\% y\) là lượng lipit có được là \(20\% x + 40\% y\).
Vì gia đình đó cần ít nhất \(0,9kg\) chất protein và \(0,4kg\)chất lipit trong thức ăn mỗi ngày nên điều kiện tương ứng là \(80\% x + 60\% y \ge 0,9\)và \(20\% x + 40\% y \ge 0,4\)hay \(4x + 3y \ge 4,5\) và \(x + 2y \ge 2\)
Vậy x,y thỏa mãn hệ bất phương trình \(\left\langle \begin{array}{l}0 \le x \le 1,6\\0 \le y \le 1,1\\4x + 3y \ge 4,5\\x + 2y \ge 2\end{array} \right.\) (*)
Khi đó bài toán trở thành:
Trong các nghiệm của hệ bất phương trình (*), tìm nghiệm (\(x = {x_{0,}}y = {y_0}\)) sao cho \(T = 45x + 35y\) nhỏ nhất
Trong mặt phẳng tọa độ, ta sẽ biểu diễn phần mặt phẳng chứa điểm \(M(x,y)\) thỏa mãn (*)
Miền nghiệm của hệ (*) là miền bên trong của tứ giác lồi \(ABCD\) và cả biên (như hình vẽ)
T đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác \(ABCD\)
Ta có:
\(A(1,6;1,1),B(1,6;0,2)C(0,6;0,7),D(0,3;1)\)
Kiểm tra được \(x = 0,6;y = 0,7\) thì \(T = 51,5\) (nghìn đồng) là nhỏ nhất.
Vậy gia đình đó mua \(0,6kg\) thịt bò và \(0,7kg\) thịt lợn thì chi phí là ít nhất. Cụ thể là phải chi phí 51,5 nghìn đồng
Đáp án cần chọn là: B
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
