Một cây cầu treo có trọng lượng phân bố đều dọc theo chiều dài của nó. Cây cầu có trụ

Câu hỏi số 582923:

Vận dụng cao

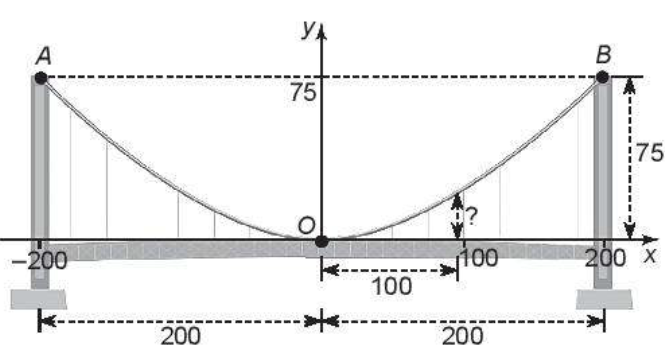
Một cây cầu treo có trọng lượng phân bố đều dọc theo chiều dài của nó. Cây cầu có trụ tháp đôi cao 75m so với mặt của cây cầu và cách nhau 400m. Các dây cáp có hình dạng parabol và được treo trên các đỉnh tháp. Các dây cáp chạm mặt cầu ở tâm của cây cầu. Tìm chiều cao của dây cáp tại điểm cách tâm của cây cầu 100m (giả sử mặt của cây cầu là mặt phẳng).

A. 18,75m

B. 18,25m

C. 18m

D. 25m

Đáp án đúng là: A

Quảng cáo

Xem lời giải

Câu hỏi:582923

Phương pháp giải

Xác định 2 điểm thuộc đồ thị hàm số bậc hai, từ đó suy ra phương trình parabol.

Thay x = 100 tìm y.

Giải chi tiết

Theo giả thiết, cây cầu có trụ tháp đôi cao 75m so với mặt của cây cầu và cách nhau 400m nên ta có tọa độ các điểm A(-200;75) và B(200;75) thuộc parabol.

Khi đó ta có: \(75 = a{.200^2} \Rightarrow a = \dfrac{3}{{1600}}\).

Do đó, phương trình parabol là \(y = \dfrac{3}{{1600}}{x^2}\).

Với \(x = 100 \Rightarrow y = \dfrac{3}{{1600}}{.100^2} = 18,75\).

Vậy chiều cao của dây cáp tại điểm cách tâm của cây cầu 100m là 18,75m.

Đáp án cần chọn là: A

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10