Một cơ sở sản xuất dự định sản xuất ra hai loại sản phẩm A và B. Các sản phẩm này
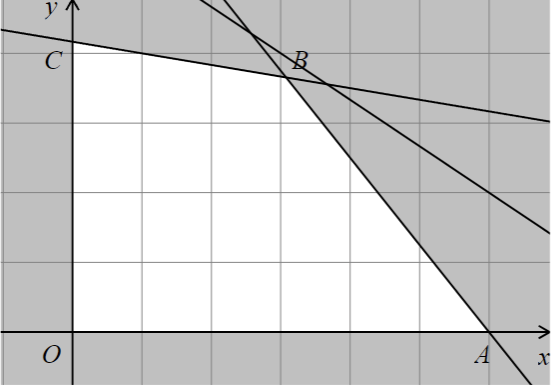
Một cơ sở sản xuất dự định sản xuất ra hai loại sản phẩm A và B. Các sản phẩm này được chế tạo ra từ ba loại nguyên liệu I, II và III. Số lượng đơn vị dự trữ của từng loại nguyên liệu và số lượng đơn vị từng loại nguyên liệu cần để sản xuất ra một đơn vị sản phẩm mỗi loại được cho tương ứng trong bảng sau:
Mỗi đơn vị sản phẩm A lãi 300000 đồng, mỗi đơn vị sản phẩm B lãi 200000 đồng. Hãy cho biết với kế hoạch sản xuất như thế nào thì số tiền lãi thu được hàng tuần là lớn nhất.
Đáp án đúng là: C
Quảng cáo
Gọi x, y lần lượt là số sản phẩm A và B mà đơn vị này sản xuất hàng tuàn \(\left( {x,y \ge 0} \right)\).
Lợi nhuận thu được hàng tuần là: \(f\left( {x;y} \right) = 300000x + 200000y\) (đồng)
Ta có hệ bất phương trình sau: \(\left\{ \begin{array}{l}2x + 3y \le 18\\5x + 4y \le 30\\x + 6y \le 25\\x,y \ge 0\end{array} \right.\,\,\left( * \right)\)
Bài toán trở thành tìm GTLN của hàm số f(x;y) trên miền nghiệm của hệ bất phương trình (*).
Miền nghiệm của hệ bất phương trình (*) là miền tứ giác OABC (kể cả biên).
Hàm số f(x;y) sẽ đạt GTLN khi (x;y) là tọa độ của một trong các đỉnh O(0;0), A(6;0), \(B\left( {\dfrac{{11}}{3};\dfrac{{32}}{9}} \right)\), \(D\left( {0;\dfrac{{25}}{6}} \right)\).
Ta có: \(f\left( {0;0} \right) = 0,\,\,f\left( {6;0} \right) = 180000,\) \(f\left( {\dfrac{{11}}{3};\dfrac{{32}}{9}} \right) = \dfrac{{16300000}}{9}\), \(f\left( {0;\dfrac{{25}}{6}} \right) = \dfrac{{2500000}}{3}\).
Suy ra f(x;y) lớn nhất khi \(\left( {x;y} \right) = \left( {\dfrac{{11}}{3};\dfrac{{32}}{9}} \right)\), tức là xưởng sản xuất 33 sản phẩm loại A và 32 sản phẩm loại B trong vòng 9 tuần để thu lợi nhuận cao nhất.
Đáp án cần chọn là: C
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
