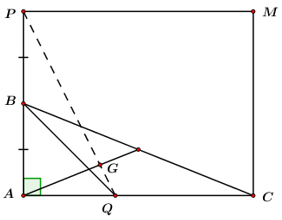
Cho \(\Delta ABC\) vuông tại \(A\) có độ dài các cạnh \(AB = 2\,cm,\,\,AC = 5cm.\) Gọi \(P\) là điểm

Câu hỏi số 434413:

Vận dụng

Cho \(\Delta ABC\) vuông tại \(A\) có độ dài các cạnh \(AB = 2\,cm,\,\,AC = 5cm.\) Gọi \(P\) là điểm đối xứng với \(A\) qua \(B;\) điểm \(Q\) trên cạnh \(AC\) sao cho \(AQ = \dfrac{2}{5}AC.\)

a) Chứng minh rằng \(5\overrightarrow {PQ} + 10\overrightarrow {AB} - 2\overrightarrow {AC} = \overrightarrow 0 .\)

b) Tính độ dài các vecto \(\overrightarrow u = \overrightarrow {AB} - \dfrac{2}{5}\overrightarrow {AC} \) và \(\overrightarrow v = \overrightarrow {AB} + 2\overrightarrow {AC} - \overrightarrow {BC} .\)

c) Chứng minh rằng đường thẳng \(PQ\) đi qua trọng tâm \(G\) của tam giác \(ABC.\)

Quảng cáo

Xem lời giải

Câu hỏi:434413

Phương pháp giải

a) Từ giả thiết, sửu dụng quy tắc chèn điểm để biến đổi các vetco để chứng minh đẳng thức.

b) Biến đổi các vecto \(\overrightarrow u ,\,\,\overrightarrow v \) rồi tính độ dài các vetco.

c) Biểu diễn \(\overrightarrow {GP} ,\,\,\overrightarrow {QP} \) theo \(\overrightarrow {AB} ,\,\,\overrightarrow {AC} .\)

Ba điểm \(G,\,\,P,\,\,Q\) thẳng hàng \( \Leftrightarrow \overrightarrow {GP} = k\overrightarrow {QP} \,\,\left( {k \ne 0} \right).\)

Giải chi tiết

a) Chứng minh rằng \(5\overrightarrow {PQ} + 10\overrightarrow {AB} - 2\overrightarrow {AC} = \overrightarrow 0 .\)

Ta có:

\(\begin{array}{l}\,\,\,\,\,5\overrightarrow {PQ} + 10\overrightarrow {AB} - 2\overrightarrow {AC} \\ = 5\overrightarrow {PA} + 5\overrightarrow {AQ} + 10\overrightarrow {AB} - 2\overrightarrow {AC} \\ = 5\overrightarrow {AQ} - 5\overrightarrow {AP} + 10\overrightarrow {AB} - 2\overrightarrow {AC} \\ = 5.\dfrac{2}{5}\overrightarrow {AC} - 5.2\overrightarrow {AB} + 10\overrightarrow {AB} - 2\overrightarrow {AC} \\ = \overrightarrow 0 \,\,\,\left( {dpcm} \right).\end{array}\)

b) Tính độ dài các vecto \(\overrightarrow u = \overrightarrow {AB} - \dfrac{2}{5}\overrightarrow {AC} \) và \(\overrightarrow v = \overrightarrow {AB} + 2\overrightarrow {AC} - \overrightarrow {BC} .\)

Ta có: \(\overrightarrow u = \overrightarrow {AB} - \dfrac{2}{5}\overrightarrow {AC} = \overrightarrow {AB} - \overrightarrow {AQ} = \overrightarrow {QB} \)

\( \Rightarrow \left| {\overrightarrow u } \right| = \left| {\overrightarrow {QB} } \right| = QB\)

Áp dụng định lý Pitago cho \(\Delta ABQ\) vuông tại \(A\) ta có:

\(\begin{array}{l}B{Q^2} = A{B^2} + A{Q^2} = A{B^2} + {\left( {\dfrac{2}{5}AC} \right)^2}\\\,\,\,\,\,\,\,\,\,\,\,\, = {2^2} + {\left( {\dfrac{2}{5}.5} \right)^2} = 8\\ \Rightarrow BQ = \sqrt 8 = 2\sqrt 2 \\ \Rightarrow \left| {\overrightarrow u } \right| = 2\sqrt 2 .\end{array}\)

\(\begin{array}{l}\overrightarrow v = \overrightarrow {AB} + 2\overrightarrow {AC} - \overrightarrow {BC} \\\,\,\,\,\, = \overrightarrow {AB} + 2\overrightarrow {AC} - \left( {\overrightarrow {BA} + \overrightarrow {AC} } \right)\\\,\,\,\,\, = \overrightarrow {AB} + 2\overrightarrow {AC} + \overrightarrow {AB} - \overrightarrow {AC} \\\,\,\,\,\, = 2\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AP} + \overrightarrow {AC} \\\,\,\,\,\, = \overrightarrow {AM} \\ \Rightarrow \left| {\overrightarrow v } \right| = AM.\end{array}\)

Với \(M\) là điểm thỏa mãn \(APMC\) là hình chữ nhật.

\( \Rightarrow AM = PC\) (tính chất hình chữ nhật).

Áp dụng định lý Pitago cho \(\Delta APC\) vuông tại \(A\) ta có:

\(\begin{array}{l}A{P^2} = A{P^2} + A{C^2} = {\left( {2AB} \right)^2} + A{C^2}\\\,\,\,\,\,\,\,\,\,\,\,\, = {\left( {2.2} \right)^2} + {5^2} = 41\\ \Rightarrow AP = \sqrt {41} \\ \Rightarrow \left| {\overrightarrow v } \right| = \sqrt {41} .\end{array}\)

c) Chứng minh rằng đường thẳng \(PQ\) đi qua trọng tâm \(G\) của tam giác \(ABC.\)

Vì \(G\) là trọng tâm \(\Delta ABC\) nên ta có: \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)

\(\begin{array}{l}\,\,\,\,\,\,\,\overrightarrow {GA} + \overrightarrow {GA} + \overrightarrow {AB} + \overrightarrow {GA} + \overrightarrow {AC} = \overrightarrow 0 \\ \Leftrightarrow 3\overrightarrow {GA} + \overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {GA} = - \dfrac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\end{array}\)

\(\begin{array}{l} \Rightarrow \overrightarrow {GP} = \overrightarrow {GA} + \overrightarrow {AP} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = - \dfrac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) + 2\overrightarrow {AB} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{5}{3}\overrightarrow {AB} - \dfrac{1}{3}\overrightarrow {AC} .\end{array}\)

\(\overrightarrow {QP} = \overrightarrow {QA} + \overrightarrow {AP} = - \dfrac{2}{5}\overrightarrow {AC} + 2\overrightarrow {AB} \)

\( \Rightarrow \overrightarrow {GP} = \dfrac{5}{6}\overrightarrow {QP} \)

\( \Rightarrow G,\,\,P,\,\,Q\) thẳng hàng hay \(PQ\) đi qua trọng tâm \(G\) của \(\Delta ABC.\) (đpcm)

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10