Một con lắc lò xo gồm vật m có khối lượng 300 g mắc vào lò xo độ cứng k = 50 N/m có thể dao
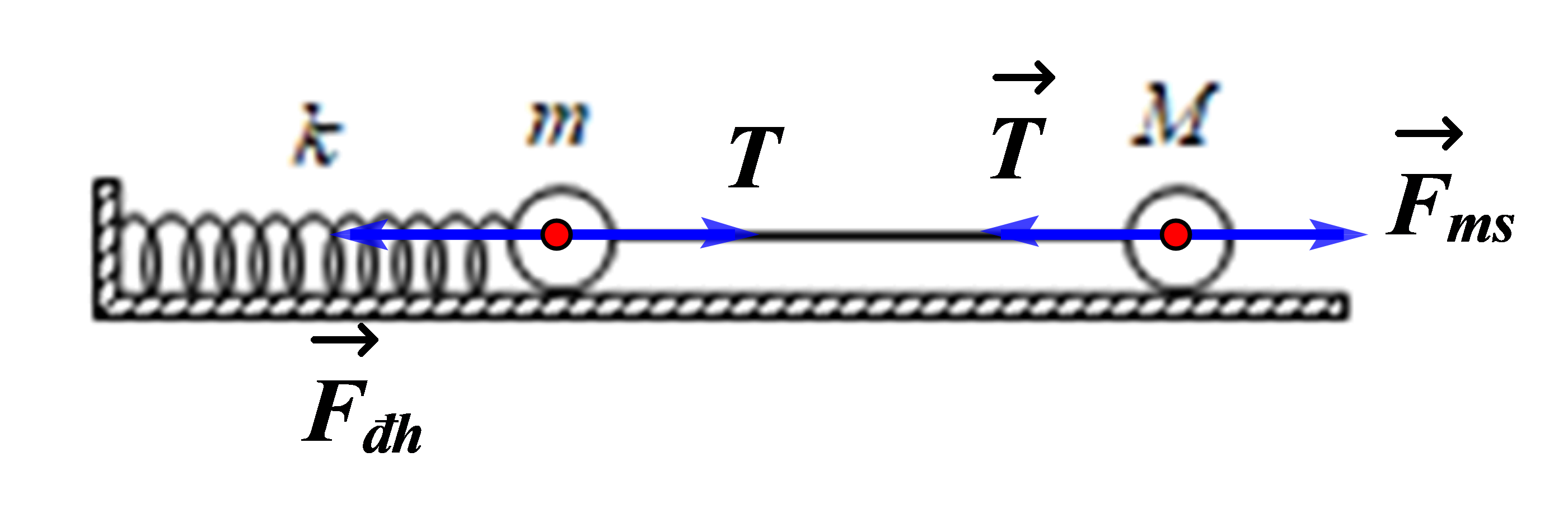
Một con lắc lò xo gồm vật m có khối lượng 300 g mắc vào lò xo độ cứng k = 50 N/m có thể dao động không ma sát trên mặt phẳng nằm ngang. Vật M khối lượng 200g được nối với vật m bằng một sợi dây nhẹ, dài và không dãn như hình vẽ. Hệ số ma sát trượt giữa M và sàn là \({\mu _t} = 0,5\). Lúc đầu vật m được giữ ở vị trí lò xo dãn 8cm (trong giới hạn đàn hồi), sợi dây căng. Thả nhẹ vật m để hệ chuyển động. Lấy \(g = 10\,\,m/{s^2}\). Độ nén cực đại của lò xo trong quá trình dao động là
Đáp án đúng là: B
Quảng cáo
Độ lớn lực ma sát là: \({F_{ms}} = \mu Mg\)
Viết phương trình định luật II Niuton cho hai vật từ đó tính được vị trí dây trùng.
Áp dụng bảo toàn năng lượng cho hệ vật và bảo toàn cơ năng cho vật m.
Độ lớn lực ma sát là:
\({F_{ms}} = \mu Mg = 0,5.0,2.10 = 1\,\,\left( N \right)\)
Tác dụng vào vật m có:
\(\overrightarrow T + \overrightarrow {{F_{dh}}} = m\overrightarrow {{a_m}} \)
Tác dụng vào vật M có:
\(\overrightarrow T + \overrightarrow {{F_{ms}}} = m\overrightarrow {{a_M}} \)
Chiếu hai phương trình lên chiều của lực ma sát:
\(\left\{ \begin{array}{l}{F_{ms}} - T = M{a_M}\\T - {F_{dh}} = m{a_m}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{a_m} = \dfrac{{{F_{ms}} - T}}{M}\\{a_M} = \dfrac{{T - {F_{dh}}}}{m} = \dfrac{{T - k.\Delta l}}{m}\end{array} \right.\)
Hai vật chuyển động với cùng gia tốc nên ta có:
\({a_m} = {a_M} \Rightarrow \dfrac{{T - k\Delta l}}{m} = \dfrac{{{F_{ms}} - T}}{M}\)
Khi dây trùng thì T = 0, thay vào ta được:
\( \Leftrightarrow \dfrac{{ - 50.\Delta l}}{{0,3}} = \dfrac{1}{{0,2}} \Rightarrow \Delta l = - 0,03\left( m \right) = - 3\left( {cm} \right)\)
(Vị trí dây trùng là vị trí lò xo nén 3cm)
Áp dụng bảo toàn năng lượng cho vị trí lò xo dãn 8cm và vị trí lò xo nén 3cm:
\(\begin{array}{l}\dfrac{1}{2}k.\Delta {l_{\max }}^2 - \dfrac{1}{2}k.\Delta {l^2} - \dfrac{1}{2}\left( {m + M} \right){v^2} = {F_{ms}}.\left( {\Delta {l_{\max }} - \Delta l} \right)\\ \Leftrightarrow \dfrac{1}{2}.50.0,{08^2} - \dfrac{1}{2}.50.0,{03^2} - \dfrac{1}{2}\left( {0,3 + 0,2} \right).{v^2} = 1.\left( {0,08 + 0,03} \right)\\ \Rightarrow \left| v \right| = \dfrac{{\sqrt {11} }}{{10}}\left( {m/s} \right)\end{array}\)
Áp dụng bảo toàn cơ năng cho vật m tại vị trí lò xo nén 3cm và lò xo nén cực đại ta được:
\(\begin{array}{l}\dfrac{1}{2}k.\Delta {l^2} + \dfrac{1}{2}m{v^2} = \dfrac{1}{2}k.\Delta {l^2}_{nen(\max )}\\ \Leftrightarrow \dfrac{1}{2}.50.0,{03^2} + \dfrac{1}{2}.0,3.{\left( {\dfrac{{\sqrt {11} }}{{10}}} \right)^2} = \dfrac{1}{2}.50.\Delta {l^2}_{nen(\max )}\\ \Rightarrow \Delta {l_{nen(\max )}} = 0,0395\left( m \right) = 3,95\left( {cm} \right)\end{array}\)
Vậy độ nén cực đại của lò xo là 3,95 cm.
Đáp án cần chọn là: B
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
