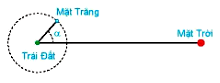
Khi Mặt Trăng quay quanh Trái Đất, mặt đối diện với Trái Đất thường chỉ được

Câu hỏi số 629695:

Vận dụng

Khi Mặt Trăng quay quanh Trái Đất, mặt đối diện với Trái Đất thường chỉ được Mặt Trời chiếu sáng một phần. Các pha của Mặt Trang được mô tả mức độ phần bề mặt của nó được Mặt Trời chiếu sáng. Khi góc giữa Mặt Trời, Trái Đất và Mặt Trăng là \(\alpha \,\,\left( {{0^0} \le \alpha \le {{360}^0}} \right)\) thì tỉ lệ F của phần Mặt Trăng đuọc chiếu sáng cho bởi công thức \(F = \dfrac{1}{2}\left( {1 - \cos \alpha } \right)\). Xác định góc \(\alpha \) tương ứng với các pha sau của Mặt Trăng:

a) F = 0 (trăng mới)

b) F = 0,25 (trăng lưỡi liềm)

c) F = 0,5 (trăng bán nguyệt đầu tháng hoặc trăng bán nguyệt cuối tháng)

d) F = 1 (trăng tròn)

Quảng cáo

Xem lời giải

Câu hỏi:629695

Phương pháp giải

\(\cos x = \cos \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = - \alpha + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\).

Giải chi tiết

a) \(F = 0 \Leftrightarrow \dfrac{1}{2}\left( {1 - \cos \alpha } \right) = 0 \Leftrightarrow \cos \alpha = 1 \Leftrightarrow \alpha = k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).

Do \({0^0} \le \alpha \le {360^0} \Rightarrow 0 \le \alpha \le 2\pi \)

\( \Rightarrow 0 \le k2\pi \le 2\pi \Rightarrow 0 \le k \le 1 \Rightarrow \left[ \begin{array}{l}k = 0 \Rightarrow \alpha = 0 = {0^0}\\k = 1 \Rightarrow \alpha = 2\pi = {360^0}\end{array} \right.\)

b) \(F = 0,25 \Rightarrow F = \dfrac{1}{2}\left( {1 - \cos \alpha } \right) = 0,25 = \dfrac{1}{4} \Leftrightarrow \cos \alpha = \dfrac{1}{2}\)\( \Leftrightarrow \left[ \begin{array}{l}\alpha = \dfrac{\pi }{3} + k2\pi \\\alpha = - \dfrac{\pi }{3} + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\)

Do \({0^0} \le \alpha \le {360^0} \Rightarrow 0 \le \alpha \le 2\pi \)

\( \Rightarrow \left[ \begin{array}{l}0 \le \dfrac{\pi }{3} + k2\pi \le 2\pi \Rightarrow - \dfrac{1}{6} \le k \le \dfrac{5}{6} \Rightarrow k = 0 \Rightarrow \alpha = \dfrac{\pi }{3} = {60^0}\\0 \le - \dfrac{\pi }{3} + k2\pi \le 2\pi \Rightarrow \dfrac{1}{6} \le k \le \dfrac{7}{6} \Rightarrow k = 1 \Rightarrow \alpha = \dfrac{{5\pi }}{3} = {300^0}\end{array} \right.\)

c) \(F = 0,5 \Rightarrow F = \dfrac{1}{2}\left( {1 - \cos \alpha } \right) = 0,5 \Leftrightarrow \cos \alpha = 0\)\( \Leftrightarrow \alpha = \dfrac{\pi }{2} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\)

Do \({0^0} \le \alpha \le {360^0} \Rightarrow 0 \le \alpha \le 2\pi \)

\( \Rightarrow 0 \le \dfrac{\pi }{2} + k\pi \le 2\pi \Rightarrow - \dfrac{1}{2} \le k \le \dfrac{3}{2} \Rightarrow \left[ \begin{array}{l}k = 0\\k = 1\end{array} \right. \Rightarrow \left[ \begin{array}{l}\alpha = \dfrac{\pi }{2} = {90^0}\\\alpha = \dfrac{{3\pi }}{2} = {270^0}\end{array} \right.\)

d) \(F = 1 \Rightarrow F = \dfrac{1}{2}\left( {1 - \cos \alpha } \right) = 1 \Leftrightarrow \cos \alpha = - 1\)\( \Leftrightarrow \alpha = \pi + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\)

Do \({0^0} \le \alpha \le {360^0} \Rightarrow 0 \le \alpha \le 2\pi \)

\( \Rightarrow 0 \le \pi + k2\pi \le 2\pi \Rightarrow - \dfrac{1}{2} \le k \le \dfrac{1}{2} \Rightarrow k = 0 \Rightarrow \alpha = \pi = {180^0}\)

Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.