Trong một lần chơi đá bóng ở trường, tại một thời điểm nào đó, An đứng ở điểm A trên

Câu hỏi số 681738:

Vận dụng cao

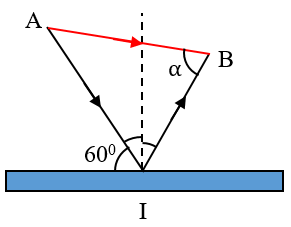
Trong một lần chơi đá bóng ở trường, tại một thời điểm nào đó, An đứng ở điểm A trên sân bóng nằm ngang, đá một quả bóng với vận tốc không đổi u = 8 m/s theo phương ngang hợp với bức tường thẳng đứng một góc \(\alpha = {60^0}\). Coi sự va chạm của bóng vào bức tường tại điểm I giống như hiện tượng phản xạ của tia sáng trên gương phẳng và sau va chạm bóng lăn với tốc độ không đổi u = 8 m/s. Ngay sau khi đá bóng, An liền chạy theo một đường thẳng với tốc độ không đổi để đón quả bóng phản xạ từ bức tường trong khi đang chạy.

a) Nếu An chọn con đường ngắn nhất để đón bóng thì vận tốc của bạn ấy phải là bao nhiêu?

b) An có thể chạy với vận tốc nhỏ nhất là bao nhiều và theo phương nào để đón được bóng?

Quảng cáo

Xem lời giải

Câu hỏi:681738

Phương pháp giải

Quãng đường của chuyển động đều: s = v.t

Định lí hàm sin: \(\dfrac{a}{{\sin \widehat A}} = \dfrac{b}{{\sin \widehat B}} = \dfrac{c}{{\sin \widehat C}}\)

Định lí hàm cos: \({a^2} = {b^2} + {c^2} - 2bc\cos \widehat A\)

Bất đẳng thức Cauchy: \({a^2} + {b^2} \ge 2ab\) (dấu “=” xảy ra \( \Leftrightarrow a = b\))

Giải chi tiết

Gọi điểm mà An đón được quả bóng là B

Ta có hình vẽ:

Từ hình vẽ ta thấy:

\(\widehat {AIB} = 2.\left( {{{90}^0} - {{60}^0}} \right) = {60^0}\)

Bạn An đón được quả bóng khi thời gian chuyển động của bạn An bằng thời gian chuyển động của quả bóng:

\(\dfrac{{AI + IB}}{u} = \dfrac{{AB}}{v}\,\,\left( * \right)\)

a) Áp dụng định lí hàm sin, ta có:

\(\begin{array}{l}\dfrac{{AB}}{{\sin \widehat {AIB}}} = \dfrac{{AI}}{{\sin \alpha }} \Rightarrow AB.\sin \alpha = AI.\sin {60^0}\\ \Rightarrow AB = \dfrac{{AI.\sin {{60}^0}}}{{\sin \alpha }}\\ \Rightarrow A{B_{\min }} \Leftrightarrow {\left( {\sin \alpha } \right)_{\max }} = 1 \Rightarrow \alpha = {90^0}\\ \Rightarrow A{B_{\min }} = AI.\sin {60^0} = \dfrac{{AI.\sqrt 3 }}{2}\\ \Rightarrow IB = AI.\cos {60^0} = \dfrac{{AI}}{2}\end{array}\)

Thay vào (*) ta có:

\(\begin{array}{l}\dfrac{{AI + 0,5AI}}{u} = \dfrac{{AI.\sqrt 3 }}{{2v}} \Rightarrow \dfrac{3}{{2u}} = \dfrac{{\sqrt 3 }}{{2v}} \Rightarrow v = \dfrac{u}{{\sqrt 3 }}\\ \Rightarrow v = \dfrac{8}{{\sqrt 3 }} \approx 4,6\,\,\left( {m/s} \right)\end{array}\)

b) Từ (*) ta có:

\(v = u.\dfrac{{AB}}{{AI + IB}} \Rightarrow {v_{\min }} \Leftrightarrow \left( {\dfrac{{AB}}{{AI + IB}}} \right)\min \)

Áp dụng định lí hàm cos cho tam giác AIB, ta có:

\(\begin{array}{l}A{B^2} = A{I^2} + I{B^2} - 2AI.IB.\cos {60^0}\\ \Rightarrow A{B^2} = A{I^2} + I{B^2} - AI.IB\\ \Rightarrow \dfrac{{A{B^2}}}{{{{\left( {AI + IB} \right)}^2}}} = \dfrac{{A{I^2} + I{B^2} - AI.IB}}{{{{\left( {AI + IB} \right)}^2}}}\\ \Rightarrow \dfrac{{A{B^2}}}{{{{\left( {AI + IB} \right)}^2}}} = 1 - \dfrac{{3AI.IB}}{{{{\left( {AI + IB} \right)}^2}}}\end{array}\)

Áp dụng bất đẳng thức Cauchy, ta có:

\(\begin{array}{l}AI + IB \ge 2\sqrt {AI.IB} \\ \Rightarrow {\left( {AI + IB} \right)^2} \ge 4.AI.IB\\ \Rightarrow \dfrac{{AI.IB}}{{{{\left( {AI + IB} \right)}^2}}} \le \dfrac{1}{4}\\ \Rightarrow \dfrac{{A{B^2}}}{{{{\left( {AI + IB} \right)}^2}}} \le 1 - \dfrac{3}{4}\\ \Rightarrow \dfrac{{AB}}{{AI + IB}} \le \dfrac{1}{2}\end{array}\)

Dấu “=” xảy ra \( \Leftrightarrow AI = IB\))

\(\begin{array}{l}\left( {\dfrac{{AB}}{{AI + IB}}} \right)\min = \dfrac{1}{2} \Rightarrow {v_{\min }} = \dfrac{1}{2}u\\ \Rightarrow {v_{\min }} = \dfrac{1}{2}.8 = 4\,\,\left( {m/s} \right)\end{array}\)

Mặt khác: AI = IB → tam giác AIB đều → AB song song với tường

Vậy bạn An có thể chạy với vận tốc nhỏ nhất là 4 m/s theo phương song song với tường để có thể đón được bóng

PH/HS 2K10 THAM GIA NHÓM ĐỂ CẬP NHẬT ĐIỂM THI, ĐIỂM CHUẨN MIỄN PHÍ!

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link