Đánh giá năng lực Hà Nội
Đánh giá năng lực Hà Nội
Một hồ nược nhân tạo được xây dựng trong một công viên giải trí.
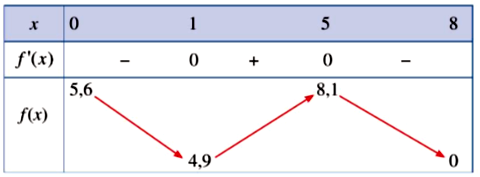
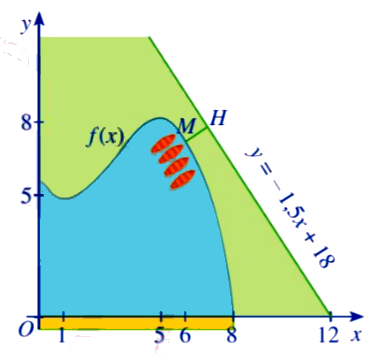
Một hồ nược nhân tạo được xây dựng trong một công viên giải trí. Trong mô hình minh hoạ, nó được giơi hạn bởi các trục tọa độ và đồ thị của hàm số \(y = f(x) = \dfrac{1}{{10}}\left( { - {x^3} + 9{x^2} - 15x + 56} \right)\). Đơn vị đo độ dài trên mỗi trục tọa độ là \(100\;{\rm{m}}\) (Nguồn:A. Bigalke et al, Mathematik, Gnundlaurs ma-1, Cornelsen 2010).
| Đúng | Sai | |
|---|---|---|
| 1) a) Đường dạo ven hồ chạy dọc theo trục Ox dài 800 mét |
||
| 2) b) Tại điểm (5,8) trên đường đi dạo ven hồ (chạy dọc theo trục Ox ) thì khoảng cách theo phương thẳng đứng đến bờ hồ đối diện là lớn nhất |
||
| 3) c) Khoảng cách lớn nhất đó theo phương thẳng đứng từ một điểm trên đường đi dạo ven hồ (chạy dọc theo trục Ox ) đến bờ hồ đối diện là 500m. |
||
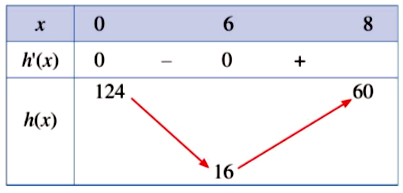
| 4) d) Trong công viên có một con đường chạy dọc theo đồ thị hàm số \(y = - 1,5x + 18\). Người ta dự định xây dựng bên bờ hồ một bến thuyền đạp nược sao cho khoảng cách từ bến thuyển đến con đường này là ngắn nhất. Toạ độ của điểm để xây bến thuyền này là \(M(6;7,4)\) |
Đáp án đúng là: 1Đ, 2S, 3Đ, 4Đ
a) Trong Hình vẽ , đồ thị của hàm số \(y = f(x) = \dfrac{1}{{10}}\left( { - {x^3} + 9{x^2} - 15x + 56} \right)\) cắt tia Ox tại điểm có hoành độ \(x = 8\). Vậy đường dạo ven hồ chạy dọc theo trục Ox dài \(800\;{\rm{m}}\).
b) Ta khảo sát hàm số: \(f(x) = \dfrac{1}{{10}}\left( { - {x^3} + 9{x^2} - 15x + 56} \right)\) với \(0 \le x \le 8\).
\(\begin{array}{l}{f^\prime }(x) = \dfrac{1}{{10}}\left( { - 3{x^2} + 18x - 15} \right)\\{f^\prime }(x) = 0 \Leftrightarrow - {x^2} + 6x - 5 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 5\end{array} \right.\end{array}\)
Bảng biến thiên:
Căn cứ bảng biến thiên, ta có: \({\max _{[0;8]}}f(x) = f(5) = 8,1\) tại \(x = 5\).
Vậy khoảng cách lớn nhất theo phương thẳng đứng từ một điểm trên đường đi dạo ven hồ (chạy dọc theo trục Ox ) đến bờ hồ đối diện là:
\({\rm{ 100}}{\rm{. }}\left. {{{\max }_{[0;8]}}f(x)} \right) = 100 \cdot f(5) = 100 \cdot 8,1 = 810(\;{\rm{m}})\)
và đạt được tại điểm trên đường đi dạo ven hồ cách gốc O một khoảng cách là \(500\;{\rm{m}}\).
d) Xét điểm \(M(x;f(x))\) thuộc đồ thị hàm số \(y = f(x) = \dfrac{1}{{10}}\left( { - {x^3} + 9{x^2} - 15x + 56} \right)\) với \(0 \le x \le 8\).
Khoảng cách từ điểm \(M(x;f(x))\) đến đường thẳng \(y = - 1,5x + 18 \Leftrightarrow - 1,5x - y + 18 = 0\) là:
\(MH = \dfrac{{\left| { - 1,5x - \dfrac{1}{{10}}\left( { - {x^3} + 9{x^2} - 15x + 56} \right) + 18} \right|}}{{\sqrt {{{( - 1,5)}^2} + {{( - 1)}^2}} }} = \dfrac{{\left| {{x^3} - 9{x^2} + 124} \right|}}{{10\sqrt {3,25} }}{\rm{. }}\)
Ta khảo sát hàm số: \(h(x) = {x^3} - 9{x^2} + 124\) với \(0 \le x \le 8\).
\(\begin{array}{l}{h^\prime }(x) = 3{x^2} - 18x\\{h^\prime }(x) = 0 \Leftrightarrow {x^2} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0{\rm{ }}\\x = 6\end{array} \right..\end{array}\)
Bảng biến thiên
Căn cứ bảng biến thiên, ta có: \(h(x) > 0\) với \(0 \le x \le 8\);
\({\min _{[0;8]}}h(x) = h(6) = 16{\rm{ }}\) tại \(x = 6\).
Do đó, \(\min MH = {\min _{[0;8]}}\dfrac{{\left| {{x^3} - 9{x^2} + 124} \right|}}{{10\sqrt {3,25} }} = \dfrac{1}{{10\sqrt {3,25} }} \cdot {\min _{[0;8]}}h(x) = \dfrac{{16}}{{10\sqrt {3,25} }} \approx 0,8875\) và đạt được tại \(x = 6\). Khi đó, \(f(6) = 7,4\).
Vậy trong mặt phẳng toạ độ Oxy ở Hình 25 , điểm để xây bến thuyền có toạ độ là \(M(6;7,4)\).
Vậy a đúng, b sai, c đúng, d đúng.
Tham Gia Group Dành Cho 2K7 luyện thi Tn THPT - ĐGNL - ĐGTD
>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
