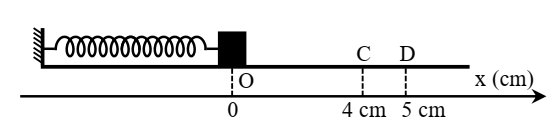
Cho cơ hệ như hình vẽ: lò xo có độ cứng k = 50 N/m, vật nặng khối lượng m = 200 g, bề mặt

Câu hỏi số 706104:

Vận dụng cao

Cho cơ hệ như hình vẽ: lò xo có độ cứng k = 50 N/m, vật nặng khối lượng m = 200 g, bề mặt chỉ có ma sát trên đoạn CD, biết OC = 4 cm, OD = 5 cm và μ = 0,5 (hình vẽ). Ban đầu vật nặng nằm tại vị trí lò xo không biến dạng, truyền cho vật vận tốc ban đầu v₀ = 40π cm/s dọc theo trục của lò xo hướng theo chiều lò xo giãn. Lấy \(g = 10m/{s^2}\). Tốc độ trung bình của vật nặng kể từ thời điểm ban đầu đến khi nó đổi chiều chuyển động lần thứ nhất gần nhất giá trị nào sau đây?

A. 140 cm/s.

B. 100 cm/s.

C. 70 cm/s.

D. 80 cm/s.

Đáp án đúng là: D

Quảng cáo

Xem lời giải

Câu hỏi:706104

Phương pháp giải

Xét chuyển động của vật trong các giai đoạn: từ O đến C là dao động điều hòa, từ C đến D là dao động có chịu tác dụng của ma sát, từ D đến khi đổi chiều là dao động điều hòa.

Sử dụng công thức độc lập với thời gian: \({x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} = {A^2}.\)

Giải chi tiết

Tần số góc của con lắc:

\(\omega = \sqrt {\dfrac{{50}}{{0,2}}} \approx 5\pi \left( {{\rm{rad/s}}} \right)\)

Giai đoạn 1: Vật di chuyển từ O đến C

Biên độ dao động của con lắc:

\({A_1} = \dfrac{{{v_0}}}{\omega } = \dfrac{{40\pi }}{{5\pi }} = 8\left( {cm} \right)\)

Vận tốc tại điểm C:

\({v_C} = \omega \sqrt {A_1^2 - x_{C1}^2} = 5\pi \sqrt {{8^2} - {4^2}} = 20\pi \sqrt 3 \left( {{\rm{cm/s}}} \right)\)

Giai đoạn 2: Vật chuyển động từ C đến D

Lực ma sát tác dụng lên vật:

\({F_{ms}} = \mu mg = 0,5.0,2.10 = 1\left( N \right)\)

Vị trí cân bằng dịch chuyển một đoạn:

\({\rm{OO'}} = \dfrac{{{F_{ms}}}}{k} = \dfrac{1}{{50}} = 0,02\left( m \right) = 2\left( {cm} \right)\)

Li độ của vật khi ở C lúc này: \({x_{C2}} = 4 + 2 = 6\left( {cm} \right)\)

Biên độ dao động của con lắc ở giai đoạn này:

\({A_2} = \sqrt {x_{C2}^2 + \dfrac{{v_C^2}}{{{\omega ^2}}}} = \sqrt {{6^2} + {{\left( {\dfrac{{20\pi \sqrt 3 }}{{5\pi }}} \right)}^2}} = 2\sqrt {21} \left( {cm} \right)\)

Li độ dao động của con lắc khi đến D là: \({x_{D2}} = 5 + 2 = 7\left( {cm} \right)\)

Vận tốc tại D:

\({v_D} = \omega \sqrt {A_2^2 - x_{D2}^2} = 5\pi \sqrt {{{\left( {2\sqrt {21} } \right)}^2} - {7^2}} = 5\pi \sqrt {35} \left( {{\rm{cm/s}}} \right)\)

Giai đoạn 3: Vật đi từ D đến khi đổi chiều:

\({A_3} = \sqrt {x_{D3}^2 + {{\left( {\dfrac{{{v_D}}}{\omega }} \right)}^2}} = \sqrt {{5^2} + {{\left( {\dfrac{{5\pi \sqrt {35} }}{{5\pi }}} \right)}^2}} = 2\sqrt {15} \left( {cm} \right)\)

Thời gian từ lúc bắt đầu dao động đến khi vật bắt đầu đổi chiều là:

\(t = \dfrac{{\arcsin \dfrac{{{x_{C1}}}}{{{A_1}}} + \arccos \dfrac{{{x_{C2}}}}{{{A_2}}} - \arccos \dfrac{{{x_{D2}}}}{{{A_2}}} + \arccos \dfrac{{{x_{D3}}}}{{{A_3}}}}}{\omega }\)

Thay số vào biểu thức tính t ta được:

\(\begin{array}{l}t = \dfrac{{\arcsin \dfrac{4}{8} + \arccos \dfrac{6}{{2\sqrt {21} }} - \arccos \dfrac{7}{{2\sqrt {21} }} + \arccos \dfrac{5}{{2\sqrt {15} }}}}{{5\pi }}\\ \to t \approx 0,09856\left( s \right)\end{array}\)

Vận tốc trung bình từ thời điểm bắt đầu dao động đến khi vật đổi chiều lần đầu là:

\({v_{tb}} = \dfrac{{{A_3}}}{t} = \dfrac{{2\sqrt {15} }}{{0,09856}} \approx 78,6\left( {cm/s} \right)\)

Đáp án cần chọn là: D

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.