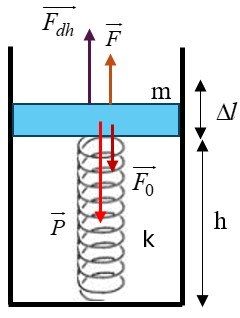
Một áp kế hình trụ, có tiết diện \(S = 10c{m^2}\) có dạng hình trụ.

Câu hỏi số 713159:

Vận dụng cao

Một áp kế hình trụ, có tiết diện \(S = 10c{m^2}\) có dạng hình trụ. Lò xo có độ cứng \(k = 100N/m\). Píttong có khối lượng 2,5kg. Bên trong chứa 0,02g khí \({H_2}\) ở áp suất khí quyển. Bỏ qua mọi ma sát. Lấy \(g = 10m/{s^2}\)

a) Đặt thẳng đứng, lò xo bị nén 2cm, nhiệt độ \({27^0}C\). Tính chiều dài tự nhiên lò xo?

b) Tăng nhiệt độ lên đến giá trị nào để lò xo có chiều dài tự nhiên?

c) Tăng nhiệt độ lên đến \({37^0}C\) mà độ biến dạng lò xo vẫn không đổi. Tính lượng khí đã bị rò ra ngoài?

Quảng cáo

Xem lời giải

Câu hỏi:713159

Phương pháp giải

+ Sử dụng phương trình Clapeyron: \(p.V = \dfrac{m}{M}.R.T\)

+ Sử dụng công thức: \(\left\{ \begin{array}{l}{F_{dh}} = k\Delta l\\F = p.S\end{array} \right.\)

Giải chi tiết

Tiết diện: \(S = 10c{m^2} = {10^{ - 3}}\left( {{m^2}} \right)\)

Độ cứng lò xo: \(k = 100N/m\)

Khối lượng pittong: \(m = 2,5kg\)

Khối lượng kí chứa trong pittong: \({m_{{H_2}}} = 0,02g\)

Áp suất khí quyển: \({p_0} = {10^5}Pa\)

a) \(\left| {\Delta l} \right| = 2cm = 0,02m;T = 300K\)

Chiều dài tự nhiên của lò xo: \({l_0} = \left| {\Delta l} \right| + h\)

Các lực tác dụng lên pittong:

+ Lực đàn hồi: \(\overrightarrow {{F_{dh}}} \)

+ Lực đẩy của khối khí bên trong pittong: \(\overrightarrow F \)

+ Lực do áp suất khí quyển gây ra: \(\overrightarrow {{F_0}} \)

+ Trọng lực: \(\overrightarrow P \)

Biểu diễn các lực tác dụng lên pittong như hình vẽ:

Khi pittong nằm cân bằng, ta có:

\(P + {F_0} = {F_{dh}} + F \Leftrightarrow P + {p_0}.S = k.\left| {\Delta l} \right| + p.S\)

\(\begin{array}{l} \Leftrightarrow mg + {p_0}.S = k.\left| {\Delta l} \right| + p.S\\ \Rightarrow p = \dfrac{{mg - k.\left| {\Delta l} \right| + {p_0}.S}}{S}\end{array}\)

\( \Rightarrow p = \dfrac{{mg - k.\left| {\Delta l} \right|}}{S} + {p_0} = \dfrac{{2,5.10 - 100.0,02}}{{{{10}^{ - 3}}}} + {10^5}\)

\( \Rightarrow p = {23.10^3} + {10^5} = 1,{23.10^5}\left( {Pa} \right)\)

Áp dụng phương trình Clapeyron ta có:

\(p.V = \dfrac{{{m_{{H_2}}}}}{M}.R.T \Rightarrow V = \dfrac{{{m_{{H_2}}}.R.T}}{{M.p}}\)

\( \Rightarrow V = \dfrac{{0,02.8,31.300}}{{2.1,{{23.10}^5}}} \approx 2,{027.10^{ - 4}}\left( {{m^3}} \right) = 2,{027.10^2}\left( {c{m^3}} \right)\)

\( \Rightarrow h = \dfrac{V}{S} = \dfrac{{2,{{027.10}^2}}}{{10}} = 20,27cm\)

\( \Rightarrow \) Chiều dài tự nhiên của lò xo:

\({l_0} = h + \left| {\Delta l} \right| = 20,27 + 2 = 22,27\left( {cm} \right)\)

Khi lò xo có chiều dài tự nhiên thì \(\Delta l = 0 \to {F_{dh}} = 0\)

\( \to \) Áp suất: \(p' = \dfrac{{mg}}{S} + {p_0} = \dfrac{{2,5.10}}{{{{10}^{ - 3}}}} + {10^5} = 1,{25.10^5}\left( {Pa} \right)\)

Thể tích của khối khí khi lò xo có chiều dài tự nhiên:

\(V = {l_0}.S = 22,27.10 = 2,{227.10^2}\left( {c{m^3}} \right) = 2,{227.10^{ - 4}}\left( {{m^3}} \right)\)

Áp dụng phương trình Clapeyron ta có:

\(p'.V = \dfrac{{{m_{{H_2}}}}}{M}.R.T \Rightarrow T = \dfrac{{p'.V.M}}{{{m_{{H_2}}}.R}} = \dfrac{{1,{{25.10}^5}.2,{{227.10}^{ - 4}}.2}}{{0,02.8,31}}\)

\( \Rightarrow T \approx 335K \Rightarrow t = 335 - 273 = 62\,\,\,\left( {^0C} \right)\)

c) Ta có: \(\left\{ \begin{array}{l}T = 37 + 273 = 300K\\\left| {\Delta l} \right| = 2cm = 0,02m\end{array} \right.\)

Thể tích của khối khí:

\(V = h.S = 20,27.10 = 202,7\left( {{m^3}} \right) = 2,{027.10^{ - 4}}\left( {{m^3}} \right)\)

Áp suất: \(p = 1,{23.10^5}\left( {Pa} \right)\)

Áp dụng phương trình Clapeyron ta có: \(p.V = \dfrac{{{m_{{H_2}}}'}}{M}.R.T\)

\( \Rightarrow {m_{{H_2}}}' = \dfrac{{p.V.M}}{{R.T}} = \dfrac{{1,{{23.10}^5}.2,{{027.10}^{ - 4}}.2}}{{8,31.310}} \approx 0,0194\left( g \right)\)

\( \Rightarrow \) Lượng khí đã bị rò ra ngoài là: \(\Delta m = 0,02 - 0,0194 = {6.10^{ - 4}}\left( g \right)\)

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.