Một xilanh thẳng đứng tiết diện $100c{m^2}$ chứa khí ở ${27^0}C$ được đậy bởi pít-tông

Câu hỏi số 721506:

Vận dụng cao

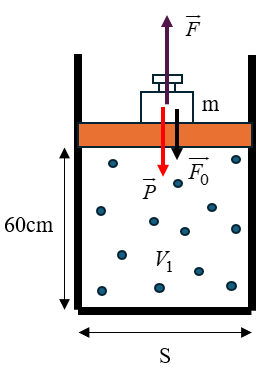
Một xilanh thẳng đứng tiết diện $100c{m^2}$ chứa khí ở ${27^0}C$ được đậy bởi pít-tông nhẹ cách đáy 60cm. Trên pít-tông có đặt một vật có khối lượng 100kg. Đốt nóng khí thêm ${50^0}C$ . Cho áp suất khí quyển là $1,{01.10^5}N/{m^2};{\rm{ }}g = 9,8m/{s^2}$ . Công do khí thực hiện là bao nhiêu J?

Quảng cáo

Xem lời giải

Câu hỏi:721506

Phương pháp giải

+ Phân tích các lực tác dụng lên vật.

+ Công do khí thực hiện là: $A = p.\Delta V$

+ Áp dụng biểu thức định luật Charles.

Giải chi tiết

Ta có: $\left\{ \begin{array}{l}{T_1} = 27 + 273 = 300K\\{T_2} = 350K\\{p_0} = 1,{01.10^5}N/{m^2};g = 9,8m/{s^2}\end{array} \right.$

Tiết diện: $S = 100\left( {c{m^2}} \right) = {10^{ - 2}}\left( {{m^2}} \right)$

$\Rightarrow$ ${V_1} = 100.60 = 6000c{m^3} = {6.10^{ - 3}}\left( {{m^3}} \right)$

Ta có: $F = {F_0} + P \Leftrightarrow p.S = {p_0}.S + P$

$\Rightarrow p = {p_0} + \dfrac{P}{S} = {p_0} + \dfrac{{mg}}{S}$

Công do khí thực hiện là: $A = p.\Delta V = \left( {{p_0} + \dfrac{{m.g}}{S}} \right).\Delta V$

Quá trình biến đổi trạng thái là quá trình đẳng áp, ta có:

$\dfrac{{{V_1}}}{{{T_1}}} = \dfrac{{{V_2}}}{{{T_2}}} \Rightarrow {V_2} = \dfrac{{{T_2}}}{{{T_1}}}.{V_1}$

$\Rightarrow \Delta V = {V_2} - {V_1} = \dfrac{{{T_2}}}{{{T_1}}}.{V_1} - {V_1} = \left( {\dfrac{{{T_2}}}{{{T_1}}} - 1} \right).{V_1}$

$\Rightarrow A = \left( {{p_0} + \dfrac{{m.g}}{S}} \right).\left( {\dfrac{{{T_2}}}{{{T_1}}} - 1} \right).{V_1}$

Thay số ta được:

$A = \left( {1,{{01.10}^5} + \dfrac{{100.9,8}}{{{{10}^{ - 2}}}}} \right).\left( {\dfrac{{350}}{{300}} - 1} \right){.6.10^{ - 3}} = 199\left( J \right)$

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD - Click xem ngay) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.