Hai dây dẫn thẳng, rất dài, đặt song song, cách nhau 20 cm trong không khí,

Câu hỏi số 725368:

Vận dụng

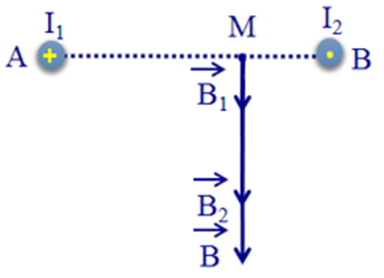
Hai dây dẫn thẳng, rất dài, đặt song song, cách nhau 20 cm trong không khí, có hai dòng điện ngược chiều, có cường độ \({I_1} = 12A;{I_2} = 15A\) chạy qua. Cảm ứng từ tổng hợp do hai dòng điện này gây ra tại điểm M cách dây dẫn mang dòng \({I_1}\) 15 cm và cách dây dẫn mang dòng \({I_2}\) 5 cm là bao nhiêu? (Đơn vị: \({10^{ - 5}}T\)).

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:725368

Phương pháp giải

+ Sử dụng quy tắc nắm bàn tay phải ta xác định được các vecto cảm ứng từ.

+ Sử dụng công thức: \(B = {2.10^{ - 7}}.\dfrac{I}{r}\).

+ Sử dụng nguyên lí chồng chất từ trường.

Giải chi tiết

Sử dụng quy tắc nắm bàn tay phải ta xác định được các vecto cảm ứng từ như hình vẽ:

Dòng điện \({I_1}\) gây ra cảm ứng từ \(\overrightarrow {{B_1}} \), dòng điện \({I_2}\) gây ra cảm ứng từ \(\overrightarrow {{B_2}} \)

Ta có: \(\left\{ \begin{array}{l}{I_1} = 12A;{I_2} = 15A\\AM = 15cm = 0,15m\\BM = 5cm = 0,05m\end{array} \right.\)

Cảm ứng từ tổng hợp tại M: \(\overrightarrow {{B_M}} = \overrightarrow {{B_1}} + \overrightarrow {{B_2}} \)

Mà \(\overrightarrow {{B_1}} \uparrow \uparrow \overrightarrow {{B_2}} \Rightarrow {B_M} = {B_1} + {B_2}\)

Trong đó: \(\left\{ \begin{array}{l}{B_1} = {2.10^{ - 7}}.\dfrac{{{I_1}}}{{AM}} = {2.10^{ - 7}}.\dfrac{{12}}{{0,15}} = 1,{6.10^{ - 5}}\left( T \right)\\{B_2} = {2.10^{ - 7}}.\dfrac{{{I_2}}}{{BM}} = {2.10^{ - 7}}.\dfrac{{15}}{{0,05}} = {6.10^{ - 5}}\left( T \right)\end{array} \right.\)

\( \Rightarrow {B_M} = 1,{6.10^{ - 5}} + {6.10^{ - 5}} = 7,{6.10^{ - 5}}\left( T \right)\)

Đáp số: 7,6.

Đáp án cần điền là: 7,6

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.