Trong mặt phẳng \(\left( {Oxy} \right)\)cho đường tròn \(\left( C \right){x^2} + {y^2} - 4x - 4y - 8 = 0\).
Trong mặt phẳng \(\left( {Oxy} \right)\)cho đường tròn \(\left( C \right){x^2} + {y^2} - 4x - 4y - 8 = 0\). Qua điểm \(T\left( {8;6} \right)\) có 2 tiếp tuyến tiếp xúc với đường tròn \(\left( C \right)\) tại \(A\) và \(B\). Đường thẳng qua 2 điểm \(A\) và \(B\) có dạng \(ax + by + 1 = 0\), thì \(b\) thuộc khoảng nào?
Đáp án đúng là: B
Quảng cáo
- Phương trình đường thẳng \(d\) đi qua \(M\left( {{x_0};{y_0}} \right)\) và có 1 VTPT \(\overrightarrow n = \left( {a;b} \right)\) là: \(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0\).
- Đường thẳng \(AB\) vuông góc với \(IT\).
- Sử dụng hệ thức lượng trong tam giác vuông, tính \(IH\).
- Tính \(d\left( {I;AB} \right)\), sử dụng công thức tính khoảng cách từ điểm \(M\left( {{x_0};{y_0}} \right)\) đến đường thẳng \(d:\,\,Ax + By + C = 0\) là: \(d\left( {M;AB} \right) = \dfrac{{\left| {A{x_0} + B{y_0} + C} \right|}}{{\sqrt {{A^2} + {B^2}} }}\).
- Giải phương trình tìm \(m\), đường thẳng \(AB\) thỏa mãn là đường thẳng mà \(I,\,\,T\) nằm khác phía đối với đường thẳng đó.
Đường tròn \(\left( C \right):{x^2} + {y^2} - 4x - 4y - 8 = 0\) có tâm \(I\left( {2;2} \right)\), bán kính \(R = \sqrt {4 + 4 - \left( { - 8} \right)} = 4\).
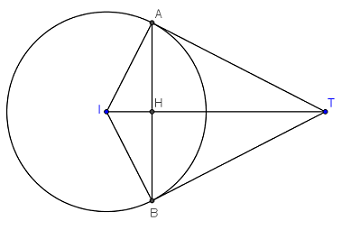
\(\overrightarrow {IT} = \left( {6;4} \right) \Rightarrow IT = \sqrt {{6^2} + {4^2}} = \sqrt {52} \)
\(AB \bot IT \Rightarrow \)Phương trình đường thẳng \(AB\) có dạng: \(3x + 2y + m = 0.\)
\(\Delta AIT\) vuông tại \(A\), \(AH\) là đường cao \( \Rightarrow I{A^2} = IH.IT \Rightarrow IH = \dfrac{{I{A^2}}}{{IT}} = \dfrac{{16}}{{\sqrt {52} }} = \dfrac{8}{{\sqrt {13} }} = d\left( {I;AB} \right)\)
\( \Rightarrow \dfrac{{\left| {3.2 + 2.2 + m} \right|}}{{\sqrt {{3^2} + {2^2}} }} = \dfrac{8}{{\sqrt {13} }} \Leftrightarrow \left| {m + 10} \right| = 8 \Leftrightarrow \left[ \begin{array}{l}m = - 2\\m = - 18\end{array} \right.\)
Với \(m = - 2 \Rightarrow AB:\,\,3x + 2y - 2 = 0\)
Ta có: \(\left( {3.2 + 2.2 - 8} \right)\left( {3.8 + 2.6 - 8} \right) > 0 \Rightarrow I,T\) nằm cùng phía so với \(AB\) \( \Rightarrow \) Loại
Với \(m = - 18 \Rightarrow AB:\,\,3x + 2y - 18 = 0\)
Ta có: \(\left( {3.2 + 2.2 - 18} \right)\left( {3.8 + 2.6 - 18} \right) < 0 \Rightarrow I,T\) nằm khác phía so với \(AB\) \( \Rightarrow \) Thỏa mãn.
Vậy phương trình đường thẳng \(AB\) là: \(3x + 2y - 18 = 0 \Leftrightarrow - \dfrac{1}{6}x - \dfrac{1}{9}y + 1 = 0\)
\( \Rightarrow b = - \dfrac{1}{9} \in \left( { - 1;0} \right)\).
Chọn: B.
Đáp án cần chọn là: B
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn

-
024.7300.7989
-
1800.6947

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com











