Hai con lắc lò xo cấu tạo giống nhau, có cùng chiều dài tự nhiên bằng 80 cm và đầu cố định

Câu hỏi số 491529:

Vận dụng cao

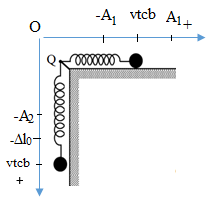
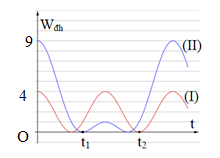
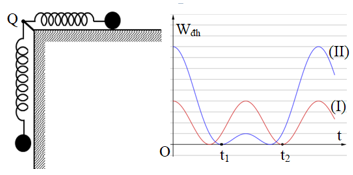
Hai con lắc lò xo cấu tạo giống nhau, có cùng chiều dài tự nhiên bằng 80 cm và đầu cố định gắn chung tại điểm Q. Con lắc (I) nằm ngang trên mặt bàn nhẵn. Con lắc (II) treo thẳng đứng cạnh mép bàn như hình vẽ. Kích thích cho hai con lắc dao động điều hòa tự do. Chọn mốc thế năng đàn hồi của mỗi con lắc tại các vị trí tương ứng của vật lúc lò xo có chiều dài tự nhiên. Thế năng đàn hồi các con lắc phụ thuộc thời gian theo quy luật được mô tả bởi đồ thị hình vẽ. Biết tại thời điểm t = 0, cả hai lò xo đều dãn và \({t_2} - {t_1} = \dfrac{\pi }{{12}}s\). Lấy g = 10 m/s². Tại thời điểm \(t = \dfrac{\pi }{10}{\mkern 1mu} s\) khoảng cách hai vật dao động gần nhất với giá trị nào sau đây?

A. 85 cm.

B. 92 cm.

C. 149 cm.

D. 125 cm.

Đáp án đúng là: B

Quảng cáo

Xem lời giải

Câu hỏi:491529

Phương pháp giải

Công thức tính thế năng: \({W_t} = \dfrac{1}{2}k{x^2}\)

Tần số góc: \(\omega = \sqrt {\dfrac{k}{m}} = \sqrt {\dfrac{g}{{\Delta {l_0}}}} \)

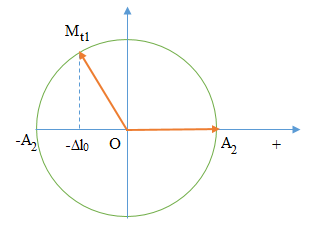
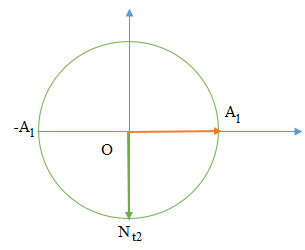
Sử dụng VTLG.

Giải chi tiết

Ta có hình vẽ, chọn hệ quy chiếu như hình vẽ:

Đồ thị thế năng đàn hồi của hai con lắc:

Từ đồ thị ta thầy đường màu đỏ cho biết thế năng đàn hồi của con lắc lò xo nằm ngang. Thế năng cực đại ứng với 4 đơn vị: \({{\rm{W}}_1} = \dfrac{1}{2}.k.A_1^2\)

Đường màu xanh là thế năng đàn hồi của con lắc lò xo treo thẳng đứng. Vì tại vị trí cân bằng lò xo đã dãn một đoạn ∆l₀ nên tại vị trí lò xo dãn nhiều nhất, thế năng đàn hồi cực đại lớn nhất ứng với 9 đơn vị: \({{\rm{W}}_{2 + }} = \dfrac{1}{2}.k.{\left( {A + \Delta {l_0}} \right)^2}\)

Tại vị trí biên trên (biên âm) thì thế năng đàn hồi ứng với 1 đơn vị:

\({{\rm{W}}_{2 - }} = \dfrac{1}{2}.k.{(A - \Delta {l_0})^2}\)

Ta có tỉ số:

\(\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{\dfrac{{{{\rm{W}}_{2 + }}}}{{{{\rm{W}}_{2 - }}}} = \dfrac{9}{1} = \dfrac{{{{\left( {{A_2} + \Delta {l_0}} \right)}^2}}}{{{{\left( {{A_2} - \Delta {l_0}} \right)}^2}}} \Leftrightarrow \dfrac{{\left( {{A_2} + \Delta {l_0}} \right)}}{{\left( {{A_2} - \Delta {l_0}} \right)}} = 3}\\{\dfrac{{{{\rm{W}}_{2 + }}}}{{{{\rm{W}}_1}}} = \dfrac{9}{4} = \dfrac{{{{\left( {{A_2} + \Delta {l_0}} \right)}^2}}}{{A_1^2}} \Leftrightarrow \dfrac{{{A_2} + \Delta {l_0}}}{{{A_1}}} = \dfrac{3}{2} \Leftrightarrow \dfrac{{3\Delta {l_0}}}{{{A_1}}} = \dfrac{3}{2}}\end{array}} \right.}\\{ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{A_2} = 2\Delta {l_0}}\\{{A_1} = 2\Delta {l_0}}\end{array}} \right. \Rightarrow {A_1} = {A_2}}\end{array}\)

Tại thời điểm ban đầu t = 0, ta thấy cả hai vật đều đang ở biên dương. Thời điểm t₁ là thời điểm vật của lò xo treo thẳng đứng đi qua vị trí lò xo không dãn.

Ta có VTLG:

Thời gian từ t = 0 đến t₁là \({t_1} = \dfrac{T}{{2\pi }}.\left( {\dfrac{\pi }{2} + \arcsin \dfrac{{\Delta {l_0}}}{{{A_2}}}} \right) = \dfrac{T}{3}\)

Thời điểm t₂ là thời điểm vật của lò xo nằm ngang đi qua vị trí cân bằng lần thứ 2.

Ta có VTLG:

Thời gian từ t = 0 đến t₂là \({t_2} = \dfrac{3}{4}T\)

Khoảng thời gian:

\({t_2} - {t_1} = \dfrac{\pi }{{12}} \Rightarrow \dfrac{3}{4}T - \dfrac{T}{3} = \dfrac{5}{{12}}T = \dfrac{\pi }{{12}} \Rightarrow T = \dfrac{\pi }{5}\left( s \right)\)

Tần số góc của hai con lắc là như nhau vì chúng đều dao động tự do và có cùng độ cứng, vật nặng cùng khối lượng:

\(\omega = \sqrt {\dfrac{k}{m}} = \sqrt {\dfrac{g}{{\Delta {l_0}}}} \)

Vậy ta có: \(\omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{{\dfrac{\pi }{5}}} = 10 = \sqrt {\dfrac{g}{{\Delta {l_0}}}} \Rightarrow \Delta {l_0} = 0,1m = 10cm\)

\( \Rightarrow {A_1} = {A_2} = 20cm\)

Sau thời gian \(t = \dfrac{\pi }{{10}}s = \dfrac{T}{2}\) thì hai vật đều đang ở biên âm.

Khoảng cách giữa hai vật lúc này là:

\(d = \sqrt {{{\left( {l - {A_1}} \right)}^2} + {{\left( {l + \Delta {l_0} - {A_2}} \right)}^2}} = \sqrt {{{\left( {80 - 20} \right)}^2} + {{\left( {80 + 10 - 20} \right)}^2}} = 92,2cm\)

Đáp án cần chọn là: B

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.